从头实现一个神经网络

从头实现一个神经网络

神经网络其实就是把多个神经元连在一起，形成一个网络。上一层神经元的输出作为下一层神经元的输入。
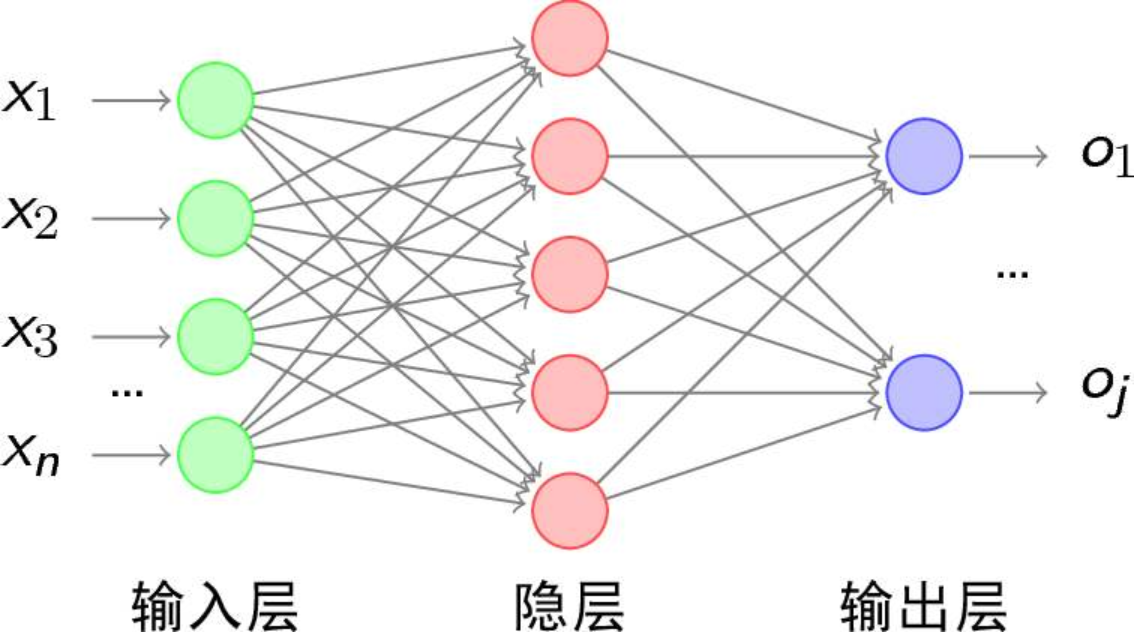
下图就是一个神经网络示意图，红色和蓝色的节点就是神经元，这是一个简单的神经网络，复杂的网络无非就是输入多一些，隐层多一些而已，本质上还是这样的。

1.神经元

神经元是神经网络的基本单元，一个神经元可以理解为对所有的输入值$(x)$加权$(w)$，然后相加，再加上偏置($\theta$),得到这一组输入的计算值，再将计算值代入到激活函数中，得到这个神经元的输出。计算值可以理解为神经元的输入所产生的刺激的强度，神经元的输出可以理解为神经元对于这个强度的刺激是否作出反应。

最原始的激活函数是阶跃函数，其函数图像如下：

这与人类的神经元的工作方式类似，即当刺激强度足够的时候，我就作出响应（输出1），当刺激强度不够的时候，我就不响应（输出0）。
但是这个函数不是连续可导的，现在常用的激活函数是Sigmoid函数，其函数图像如下所示：

Sigmoid函数的优点有单增，连续可导，其导数也单增等，因此十分适合用来做激活函数。
除了Sigmoid函数，其他常用的激活函数还有：

Tanh函数

ReLU函数

为了方便，我们以拥有两个输入的神经元为例进行讲解。

如图所示，这是一个拥有两个输入$x_1$和$x_2$的神经元，每个输入对应的权重为${\omega }_1$和${\omega }_2$，偏置设为$b$，则这个神经元对输入的计算值为
$$(x_1\times {\omega }_1)+(x_2\times {\omega }_2)+b$$
将上式代入激活函数得到该神经元的输出：
$$y=f((x_1\times {\omega }_1)+(x_2\times {\omega }_2)+b)$$
假设该神经元的两个权重${\omega }_1=0$，${\omega }_2=1$，偏置$b=4$，输入$x_1=2$,$x_2=3$,将上述值代入神经元公式，得到计算值为：
$$\begin{array}{rl}{\omega }_1\times x_1+{\omega }_2\times x_2+b& =0\times 2+1\times 3+4\\ & =7\end{array}$$
将计算值7代入激活函数Sigmoid，$Sigmoid(7)=\boxed{0.99}$。也就是说这个神经元对这一组输入$\left[\begin{array}{cc}2& 3\end{array}\right]$的输出是0.99。这种给定输入，得到输出的过程被称之为前馈。

编码实现一个神经元

使用NumPy库来帮助实现神经元。通过上边的描述可以知道，一个神经元干的事情就是对输入加权，然后加上偏置，将此计算值代入激活函数得到最终的神经元输出。输入是由外部提供的，那么神经元自身的属性其实就是权重和偏置，神经元的函数（即神经元功能）即是实现上述的计算过程，得到输出。
通过定义一个神经元类，将神经元的权重和偏置作为类的属性，生成一个具体的神经元对象的时候通过初始化函数指定该神经元的权重和偏置的具体值。还定义了前馈的具体实现，即将输入乘以权重之后相加，再加上偏置，得到计算值，将此计算值代入激活函数sigmoid，得到神经元的输出。一个基本的神经元大概就包含这些内容。

import numpy as np
# sigmoid激活函数
def sigmoid(x):
    return 1/(1+np.exp(-x))

# 神经元类
class Neuron():
#     初始化，一个神经元其实就两个参数，每个输入的权重和偏置，这是为了方便理解故意写的比较原始
#其实偏置也可以放到权重向量里，通常记为 w_0，它的输入为 x_0 = 1，这样的话神经元就只有一个参数-权重。
    def __init__(self, weights, bias):
        self.weights = weights
        self.bias = bias
    
    #定义了神经元的前馈函数，即将输入与权重相乘再加上偏置，得到的计算值再代入激活函数中，得到神经元的最终输出    
    def feedforward(self, inputs):
        #这步先计算神经元的输入的计算值，利用numpy的向量点积进行计算
        total = np.dot(self.weights, inputs) + self.bias
       #代入到激活函数sigmoid中，得到神经元的输出值
        return sigmoid(total)

if __name__ == "__main__":
#用np库的array函数生成向量 
#神经元的权重，这里只设置了2个权重，2个输入
    weights = np.array([0,1])
    bias = 4  #偏置
    
    myNeuron = Neuron(weights, bias)
    x = np.array([2,3])  #两个输入
    neuron_output = myNeuron.feedforward(x)
    print(neuron_output)

0.9990889488055994

2.将神经元组成神经网络

神经网络就是将神经元彼此连接，上一层神经元的输出作为下一层神经元的输入。还是以有两个输入的神经元为例进行说明。下图展示了一个最简单的神经网络的构成。这个神经网络有两个输入，一个隐层包含2个神经元（$h_1$和$h_2$），一个输出层，包含1个神经元（$o_1$）。$h_1$和$h_2$的输出是$o_1$的输入。

隐层是指输入和输出之间的层，可以有很多层。所谓深度学习就是隐层数很多的神经网络

前馈

现在假设每个神经元的权重均为$\omega =[0,1]$，偏置$bias$均为0，且激活函数都为sigmoid函数。那么如果输入$x=[2,3]$，整个神经网络的输出会是多少？

• 先算$h_1$和$h_2$：
  $$\begin{array}{rl}{h}_1=h_2& =sigmoid(0\times 2+1\times 3+0)\\ & =sigmoid(3)\\ & =0.9526\end{array}$$
• 再算$o_1$：
  $$\begin{array}{rl}{o}_1& =sigmoid(0\times 0.9526+1\times 0.9526+0)\\ & =sigmoid(0.9526)\\ & =\boxed{0.7216}\end{array}$$

可以看到对于输入$x=[2,3]$，整个神经网络的输出为0.7216
一个神经网络可以有任意多个层和任意多个神经元，但是其工作的基本流程都是一样的，一层一层的算，上一层的输出作为下一层的输入，最终得到整个神经网络的输出。

编码实现一个神经网络

'''
因为这个cell里调用了上一个cell定义的Neuron类且使用的NumPy库也是在上一个cell里导入的
因此如果上边的cell已经运行过了，则可以直接运行该cell，如果这次打开这个notebook以来，上一个cell还没运行过，则需要先运行上边的cell才能运行该cell
'''
#神经网络的类
class OurNeuralNetwork():
    #初始化函数，神经网络是由神经元组成的，因此初始化神经网络就是要初始化其中的神经元
    #根据假设，该神经网络由h1，h2和o1共3个神经元组成，每个神经元的权重均为w1=0,w2=1，bias=0
    #这里调用了上一个cell里定义的Neuron类来初始化神经元
    def __init__(self):
        weights = np.array([0,1])
        bias = 0
        
        self.h1 = Neuron(weights,bias)
        self.h2 = Neuron(weights,bias)
        self.o1 = Neuron(weights,bias)
    
    #定义这个神经网络的前馈，其实就是一层层求值的过程。先计算h1和h2的输出值，然后将h1和h2的输出作为o1的输入，计算得到网络最终的输出值
    def feedforward(self,x):
        out_h1 = self.h1.feedforward(x)
        out_h2 = self.h2.feedforward(x)
        out_o1 = self.o1.feedforward(np.array([out_h1, out_h2]))
        return out_o1

#生成一个实例
network = OurNeuralNetwork()
# 设置网络的输入
x = np.array([2,3])
# 调用前馈函数得到网络的输出
print(network.feedforward(x))

0.7216325609518421

可以看到程序输出也是0.7216，与我们之前的推导是一致的。

3.训练神经网络（第一部分）

如果我们有如下的输入：

Name	Weight	Height	Gender
Alice	133	65	F
Bob	160	72	M
Charlie	152	70	M
Diana	120	60	F

现在希望通过身高和体重来预测性别。还是使用上边的那个有两个输入，一个隐层，一个输出的神经网络。使用0表示Male，1表示Female，并对表中的数据进行归一处理。得到如下的数据表：

Name	Weight(减去135)	Height(减去66)	Gender
Alice	-2	-1	1
Bob	25	6	0
Charlie	17	4	0
Diana	-15	-6	1

损失函数

使用神经网络进行预测，需要衡量其预测的好不好，一般会定义一个损失函数来对其进行度量。这里我们选用均方差（MSE）作为损失函数：
$$MSE=\frac{1}{n}\sum _{i=1}^n(y_{true}-y_{pred}{)}^2\text{\hspace{1em}(3.1)}$$
其中：

• $n$代表样本的个数，即为4
• $y$代表被预测的值，即为性别
• $y_{true}$是样本真实值
• $y_{pred}$是神经网络计算输出值

好的网络就是预测值与真实值最接近的网络，也就是损失函数（均方差）最小的网络。因此：
所谓训练网络，其实就是调整网络的参数，使其损失函数最小

计算损失函数的例子

假设我们的网络永远输出0，那么对于上边的数据，其损失函数是多少？

Name	$y_{true}$	$y_{pred}$	$(y_{true}-y_{pred}{)}^2$
Alice	1	0	1
Bob	0	0	0
Charlie	0	0	0
Diana	1	0	1

根据表格，代入MSE公式，可计算得到：
$$MSE=\frac{1}{4}(1+0+0+1)=\boxed{0.5}$$

编码实现损失函数

def mse_loss(y_true, y_pred):
    return ((y_true - y_pred)**2).mean()

if __name__ == '__main__':
    y_true=np.array([1,0,0,1])
    y_pred=np.array([0,0,0,0])
    print(mse_loss(y_true, y_pred))

0.5

4.训练神经网络（第二部分）

训练神经网络就是调整网络的参数，使其预测值最接近实际值，即最小化损失函数。但是问题是，该如何调整参数？
为了简单起见，先假设数据集中只有一个样本Alice：

Name	Weight	Height	Gender
Alice	-2	-1	1

这种情况下，网络的误差为：
KaTeX parse error: No such environment: split at position 8: \begin{̲s̲p̲l̲i̲t̲}̲L=MSE &= \frac{…
将网络的权重和偏置都标记出来，网络图是这样的：

从上边的推导可以看出，网络的损失(MSE)是$y_{pred}$的函数，由网络的定义可知，$y_{pred}$又可以看做是输入权重$，，，{\omega }_1,{\omega }_2,{\omega }_3，{\omega }_4，{\omega }_5，{\omega }_6$和偏置$b_1,b_2,b_3$的函数。
这里要转换一下思路，当权重和偏置未改变的时候，网络的变量是输入$x$，给不同的输入，网络输出不同的值。而现在我们要考虑的是改变权重和偏置，使得网络在同样的输入$x$的情况下，输出值变化（更接近真实值），也就是说此时，我们应该将网络的损失函数看做是权重和偏置的函数，记为：

L ( ω 1 , ω 2 , ω 3 , ω 4 , ω 5 , ω 6 , b 1 , b 2 , b 3 ) L(\omega_1,\omega_2,\omega_3,\omega_4,\omega_5,\omega_6,b_1,b_2,b_3) L(ω