狄利克雷分布[编辑]
狄利克雷分布是一组连续多变量概率分布,是多变量普遍化的Β分布。为了纪念德国数学家约翰·彼得·古斯塔夫·勒热纳·狄利克雷(Peter Gustav Lejeune Dirichlet)而命名。狄利克雷分布常作为贝叶斯统计的先验概率。当狄利克雷分布维度趋向无限时,便成为狄利克雷过程(Dirichlet process)。
狄利克雷分布奠定了狄利克雷过程的基础,被广泛应用于自然语言处理特别是主题模型(topic model)的研究。
概率密度函数[编辑]
维度K ≥ 2的狄利克雷分布在参数α1, ..., αK > 0上、基于欧几里得空间RK-1里的勒贝格测度有个概率密度函数,定义为:
x1, ..., xK–1 > 0并且x1 + ... + xK–1 < 1,xK = 1 – x1 – ... – xK–1. 在(K − 1)维的单纯形开集上密度为0。
归一化衡量B(α)是多项Β函数,可以用Γ函数(gamma function)表示:
隐含狄利克雷分布[编辑]
隐含狄利克雷分布简称LDA(Latent Dirichlet allocation),是一种主题模型,它可以将文档集中每篇文档的主题按照概率分布的形式给出。同时它是一种无监督学习算法,在训练时不需要手工标注的训练集,需要的仅仅是文档集以及指定主题的数量k即可。此外LDA的另一个优点则是,对于每一个主题均可找出一些词语来描述它。
LDA首先由Blei, David M.、吴恩达和Jordan, Michael I于2003年提出[1],目前在文本挖掘领域包括文本主题识别、文本分类以及文本相似度计算方面都有应用。
数学模型[编辑]
LDA是一种典型的词袋模型,即它认为一篇文档是由一组词构成的一个集合,词与词之间没有顺序以及先后的关系。一篇文档可以包含多个主题,文档中每一个词都由其中的一个主题生成。
另外,正如Beta分布是二项式分布的共轭先验概率分布,狄利克雷分布作为多项式分布的共轭先验概率分布。因此正如LDA贝叶斯网络结构中所描述的,在LDA模型中一篇文档生成的方式如下:
- 从狄利克雷分布
 中取样生成文档i的主题分布
中取样生成文档i的主题分布
- 从主题的多项式分布
 中取样生成文档i第j个词的主题
中取样生成文档i第j个词的主题
- 从狄利克雷分布
 中取样生成主题
中取样生成主题 的词语分布
的词语分布
- 从词语的多项式分布
 中采样最终生成词语
中采样最终生成词语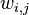
因此整个模型中所有可见变量以及隐藏变量的联合分布是
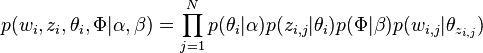
最终一篇文档的单词分布的最大似然估计可以通过将上式的 以及
以及 进行积分和对
进行积分和对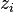 进行求和得到
进行求和得到
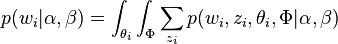
根据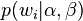 的最大似然估计,最终可以通过吉布斯采样等方法估计出模型中的参数。
的最大似然估计,最终可以通过吉布斯采样等方法估计出模型中的参数。
使用吉布斯采样估计LDA参数[编辑]
在LDA最初提出的时候,人们使用EM算法进行求解,后来人们普遍开始使用较为简单的Gibbs Sampling,具体过程如下:
- 首先对所有文档中的所有词遍历一遍,为其都随机分配一个主题,即zm,n=k~Mult(1/K),其中m表示第m篇文档,n表示文档中的第n个词,k表示主题,K表示主题的总数,之后将对应的n(k)m+1, nm+1, n(t)k+1, nk+1, 他们分别表示在m文档中k主题出现的次数,m文档中主题数量的和,k主题对应的t词的次数,k主题对应的总词数。
- 之后对下述操作进行重复迭代。
- 对所有文档中的所有词进行遍历,假如当前文档m的词t对应主题为k,则n(k)m-1, nm-1, n(t)k-1, nk-1, 即先拿出当前词,之后根据LDA中topic sample的概率分布sample出新的主题,在对应的n(k)m, nm, n(t)k, nk上分别+1。
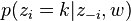 ∝
∝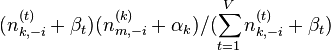
- 迭代完成后输出主题-词参数矩阵φ和文档-主题矩阵θ
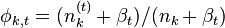
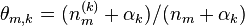
变量:
w 表示词, z 表示主题, w=(w1,w2,⋯,wN) 表示文档,语料库 D=(w1,⋯,wM) , V 表示所有单词的个数(固定值), N 表示一个文档中的词数(随机变量), M 是语料库中的文档数(固定值), k 是主题的个数(预先给定,固定值)。
在说明LDA模型之前,先介绍几个简单一些的模型。
1.Unigram model:
文档 w=(w1,w2,⋯,wN) ,用 p(wn) 表示词 wn 的先验概率,生成文档 w 的概率: p(w)=∏n=1Np(wn) 。
图模型为:

2.Mixture of unigrams model:
一篇文档只由一个主题生成。该模型的生成过程是:给某个文档先选择一个主题 z ,再根据该主题生成文档,该文档中的所有词都来自一个主题。假设主题有 z1,...,zk, 生成文档 w 的概率为:
p(w)=p(z1)∏n=1Np(wn|z1)+⋯+p(zk)∏n=1Np(wn|zk)=∑zp(z)∏n=1Np(wn|z).
图模型为:

LDA模型:
下面说明LDA模型生成一个文档的过程:
1首先要选择一个主题概率分布 θ , θ=(θ1,...,θk),θi 代表第i个主题被选择的概率,即 p(z=i|θ)=θi ,且 ∑i=1kθi=1 , θ∼Dir(α) , p(θ|α)=Γ(∑i=1kαi)∏i=1kΓ(αi)θα1−11⋯θαk−1k.
2在选好一个主题概率分布 θ 后,再选择一个主题 zn ,再根据 zn 和 β 选择一个词 wn 。 β=(βij)k×V,βij=p(wj=1|zi=1) 表示主题 i 生成词 j 的概率, ∑Vj=1βij=1 。
用2中的步骤生成N个词,文档 w 就生成了。
图模型:

由LDA的图模型我们可以清楚得看出变量间的依赖关系。
整个图的联合概率(单个文档)为: p(θ,z,,w|α,β)=p(θ|α)∏Nn=1p(zn|θ)p(wn|zn,β) ,

生成文档的概率为 p(w|α,β)=∫p(θ|α)∏Nn=1∑znp(zn|θ)p(wn|zn,β)dθ ,文本语料库由 M 篇文档组成, D=(w1,⋯,wM) ,故生成文本语料库的概率为
p(D|α,β)=∏Md=1∫p(θd|α)∏Ndn=1 ∑zdnp(zdn|θd)p(wdn|zdn,β)dθd.
下面叙述训练过程:
首先设定目标函数
我们参数训练的目标是求使 ℓ(α,β) 最大的参数 α∗,β∗ 。我们把 p(w|α,β) 展开得 p(w|α,β)=Γ(∑iαi)∏iΓ(αi)∫(∏ki=1θαi−1i)(∏Nn=1∑ki=1∏Vj=1(θiβij)wjn)dθ ,由于 θ 和 β 的耦合,对 ℓ(α,β) 用极大似然估计难以计算。下面我们用变分EM算法来计算最优参数 α,β 。
E步骤:我们用 L(γ,ϕ;α,β) 来近似估计 logp(w|α,β) ,给定一对参数值 (α,β) ,针对每一文档,求得变分参数 {γ∗d,ϕ∗d:d∈D} ,使得 L(γ,ϕ;α,β) 达到最大。
M步骤:求使 L=∑dL(γ∗d,ϕ∗d;α,β) 达到最大的 α,β 。
重复E、M步骤直到收敛,得到最优参数 α∗,β∗ 。
E步骤的计算方法:
这里用的是变分推理方法(variational inference),文档的似然函数

上式右部记为 L(γ,ϕ;α,β) 。当 p(θ,z,w|α,β)q(θ,z) 为常数时,上式取等号,即分布 q 取 p(θ,z|w,α,β) 时。
p(θ,z|w,α,β)=p(θ,z,w|α,β)p(w|α,β) ,由于 p(w|α,β) 中 θ 和 β 的耦合, p(w|α,β) 难以计算,因此 p(θ,z|w,α,β) 也难以计算。我们用分布 q(θ,z|γ,ϕ) 来近似分布 p(θ,z|w,α,β) ,在 L(γ,ϕ;α,β) 中分布 q 取 q(θ,z|γ,ϕ) ,我们得 logp(w|α,β)=L(γ,ϕ;α,β)+D(q(θ,z|γ,ϕ)||p(θ,z|w,α,β)). 上式说明计算分布 q(θ,z|γ,ϕ) 与分布 p(θ,z|w,α,β)) 间的KL距离的最小值等价于计算下界函数 L(γ,ϕ;α,β) 的最大值。
用来近似后验概率分布 p(θ,z|w,α,β)) 的分布 q(θ,z|γ,ϕ) 的图模型:

γ 为狄利克莱分布的参数, ϕ=(ϕni)n×i,n=1,⋯,N,i=1,⋯,k , ϕni 表示第 n 个词由主题 i 生成的概率, ∑ki=1ϕni=1 。
下面我们求使 L(γ,ϕ;α,β) 达到极大的参数 γ∗,ϕ∗ 。
将 L(γ,ϕ;α,β) 中的 p 和 q 分解,得

把参数 (α,β) 和 (γ,ϕ) 代入 L(γ,ϕ;α,β) ,再利用公式 Eq[log(θi)|γ]=Ψ(γi)−Ψ(∑kj=1γj) ( Ψ 是 logΓ 的一阶导数,可通过泰勒近似来计算),我们可得到

然后用拉格朗日乘子法(即变量的拉格朗日函数对变量求偏导等于零,求出变量对应的等式)来计算可得
ϕni∝βivexp(Ψ(γi)−Ψ(∑kj=1γj)),
γi=αi+∑Nn=1ϕni.
由 ∑ki=1ϕni=1 归一化求得 ϕni 。由于解 ϕni 和 γi 相互影响,可用迭代法来求解,算法如下:

最终可以得到收敛的参数 γ∗,ϕ∗ 。这里的参数 γ∗,ϕ∗ 是在给定一个固定的文档 w 下产生的,因此 γ∗,ϕ∗ 也可记为 γ∗(w),ϕ∗(w) ,变分分布 q(θ,z|γ∗(w),ϕ∗(w)) 是后验分布 p(θ,z|w,α,β) 的近似。文本语料库 D=(w1,⋯,wM) ,用上述方法求得变分参数 {γ∗d,ϕ∗d:d∈D} 。
M步骤的计算方法:
将 {γ∗d,ϕ∗d:d∈D} 代入 ∑dL(γd,ϕd;α,β) 得 L=∑dL(γ∗d,ϕ∗d;α,β) ,我们用拉格朗日乘子法求 β ,拉格朗日函数为 l=L+∑ki=1λi(∑Vj=1βij−1) ,求得 βij∝∑Md=1∑Ndn=1ϕdniwjdn ,由 ∑Vj=1βij=1 归一化求得 βij 。
下面求 α 。我们对拉格朗日函数 l 对 αi 求偏导,得 ∂l∂αi=M(Ψ(∑kj=1αj)−Ψ(αi))+∑Md=1(Ψ(γdi)−Ψ(∑kj=1γdj)) 。由这个偏导等式可知 αi 值和 αj 值( i≠j )之间相互影响,故我们得用迭代法来求解最优 α 值。我们用牛顿-拉弗逊算法来求解。将上面的偏导数再对 αj 求偏导,得 ∂l∂αi∂αj=M(Ψ′(∑kj=1αj)−δ(i,j)Ψ′(αi)) 。牛顿-拉弗逊算法的迭代公式为 αnew=αold−H(αold)−1g(αold) , H(α) 即 ∂l∂αi∂αj , g(α) 即 ∂l∂α ,迭代到收敛时即得最优 α 值。
测试新文档主题分布:
设新文档为 w ,用变分推理算法计算出新文档的 γ∗,ϕ∗ ,由于 ϕni 表示文档中第 n 个词由主题 i 生成的概率,故 ∑Nn=1ϕni 为对文档中由主题 i 生成的词数估计, 1N∑Nn=1ϕni 为主题 i 在文档主题组成中的比重。
上述说法与推导有错的话请大家批评指正。










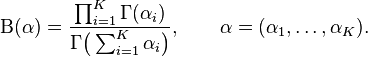















 1745
1745

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








