【格密码】最近平面算法解决CVP问题（1）

目录

一. 最近平面算法介绍

二. 简单的取整算法解决CVP问题

三. 最近平面算法

3.1 算法介绍

3.2 矩阵角度理解最近平面算法

四. 最近平面算法的图形理解

---

一. 最近平面算法介绍

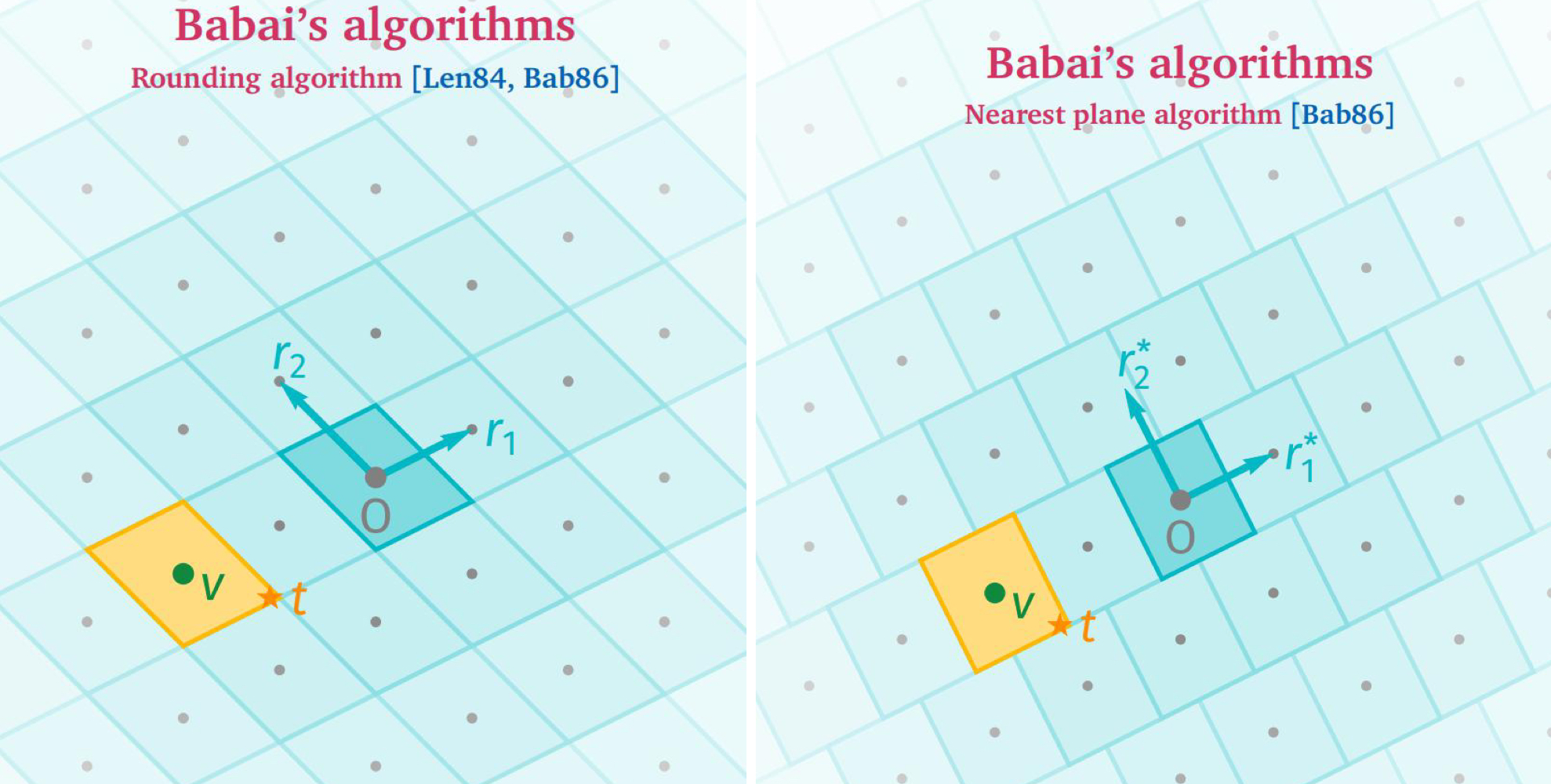
在1986年，L.Babai曾提出最近平面算法（Nearest Plane Algorithm）来解决CVP问题，利用n代表格的秩，该算法的输出近似值如下：

CVP：最近向量问题，全称Closest Vector Problem

解释：最近的格点不一定能找到，但该算法可以找到离最近格点倍的格点。这一点也说明，CVP问题在网络安全领域是困难的，很难找到最近的格点，只能是接近。

CVP问题的六种变式，如下：

当时，后三种问题就与前三种一样了。这里给出直观的解释：

计算CVP：找离其最近的格点；

优化CVP（optimization CVP）:计算出离最近格点的距离；

判定CVP（decision CVP）:判断最小距离与某值r的大小关系；

剩下的三个问题只不过加入了近似因子（approximation factor），理解起来是类似的。之所以分成这么多的版本是因为，密码学把困难问题分成了三大类：

• search问题；
• optimization问题；
• decision问题，gap问题；

如果解决了计算问题，由于计算、优化和Gap问题三者困难性一样，那么剩下的优化和Gap问题也就可以解决了。这三类问题通过调整参数是可以互相归约的。

最近平面算法可以解决近似的计算CVP问题，且此时近似因子的取值为：

为了简化分析的思路，后续仅仅讨论的情况，通过修改算法相关的参数也可以达到想要的近似值。

二. 简单的取整算法解决CVP问题

简单的取整算法就是把给定向量的系数全部直接取整（可以是上取整，也可以是下取整），该算法得到的格点与格基的选择有很大关系。

我们来看一张直观的图形：

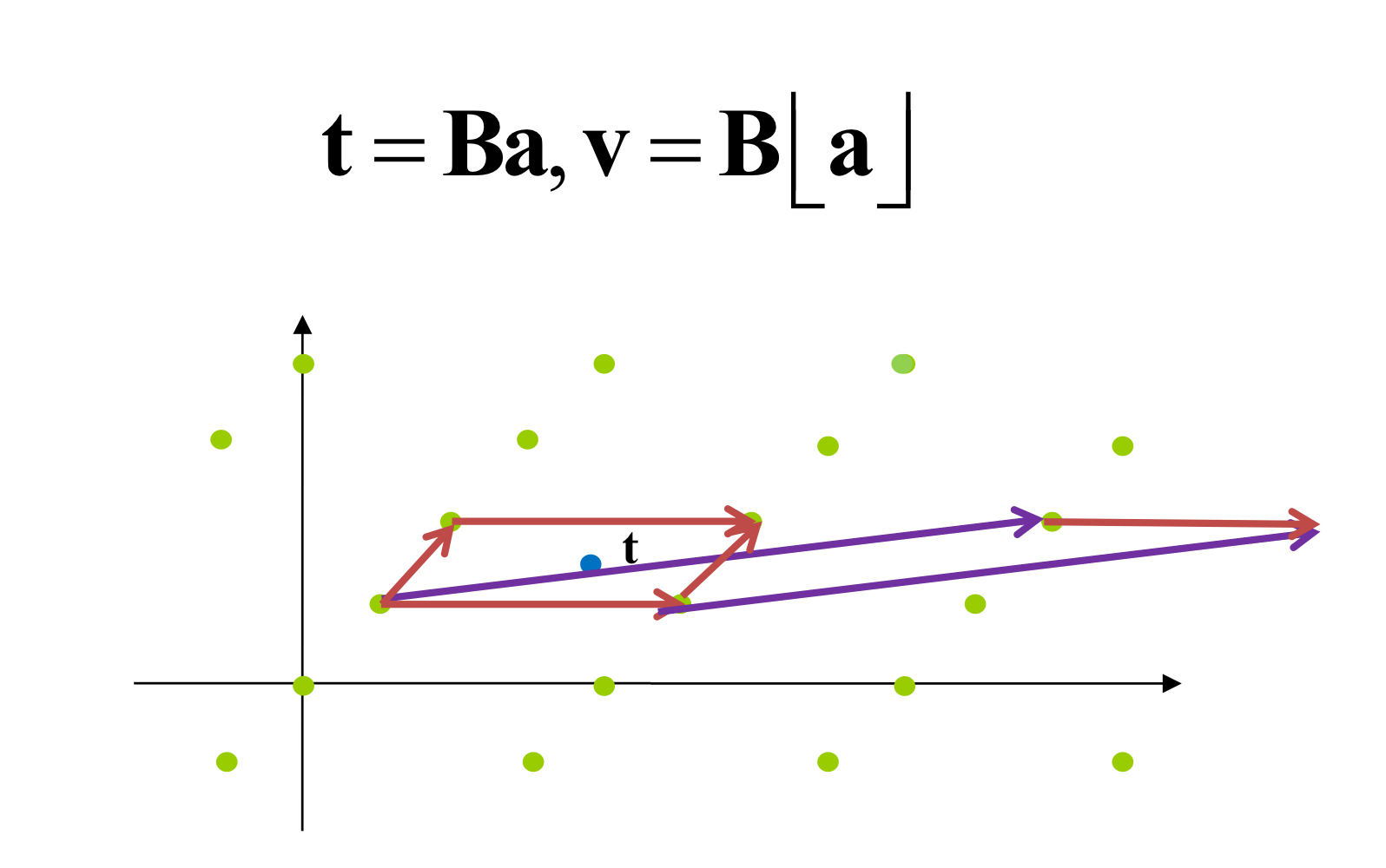
蓝色的线是原始的格基。对于任意的向量t而言，如果直接对格基进行取整的话，那么对应格点就跑到了最右端，很明显就太远了。

如果我们把格基转化一下，变成棕色线。现在对格基的系数取整得到的格点就会近很多。

以上讨论说明，格基的正交性会极大影响CVP问题的求解。这个时候也能说明LLL格基约化的重要性，推荐系列文章：

格密码LLL算法：如何解决最短向量SVP问题（1）-CSDN博客

格密码LLL算法：如何解决最短向量SVP问题（2）_lll算法复杂度-CSDN博客

格密码LLL算法：如何解决最短向量SVP问题（3）（完结篇）-CSDN博客

三. 最近平面算法

3.1 算法介绍

该算法主要有两步。

第一步针对输入的格，输出LLL约化基（LLL reduction）。

第二步，将约化后的格基进行整数线性组合，来保证与给定的向量t足够近。这个步骤跟LLL算法的内循环约化操作很类似。

算法步骤如下：

这里给一个简单的分析：

输入m行n列的格基，给定任意的m维空间实数点。需要注意的是格点也肯定是m维的；

第一步希望把格基尽量正交，其中参数选择3/4，具体理解请参看前面LLL格基约化的文章；

第二步：迭代结构，从n维到1维，不断实现降维的过程。其中的计算如下:

这一步是最近平面算法的核心精髓，可以利用投影的思想来解释，然后进行就近取整。

最后一步剩下的b就是实数点和格点之间的向量，所以t-b即为最终的格点。

显然，前面已经证明LLL算法（第一步）与约化步骤的算法（第二步）都属于多项式时间算法，由此可得该最近平面算法与输入的规模n之间也是多项式时间关系。以下的讨论分析将包含满秩格与非满秩格。

3.2 矩阵角度理解最近平面算法

给定单位正交基（orthonormal set），如下：

对于满秩的格来讲，这个格基可以直接形成全部整数格点.其中“~”代表正交化。

对于非满秩格来讲，假定m大于n，那么格基的列向量也要形成m维。换句话，则需要增加m-n行零向量。由此对应的矩阵B与组合形成的t如下：

第一个代表约化后的格基矩阵；

第二个列向量代表格基的线性组合，因为向量t不一定为格点，所以这种组合可能非整数。

最近平面算法则是寻求对矩阵B列向量的整数组合，为保求出的格点与向量t足够近，其整数组合肯定是需要限定范围的，如下：

该算法是先从第n列开始，对于这一列向量的整数，则是介于：

接着计算第n-1列，不断往格基矩阵的左边递推计算。整个迭代过程需要重复n次。

根据线性代数的基础知识，我们知道如果为非满秩格，那么余下的m-n维空间则是与原格的扩展空间是垂直的。

四. 最近平面算法的图形理解

举一个3维的例子，通过最近平面算法降到2维，如下图：

算法的核心思想可以分成四步： 

1. 考虑非满秩格，首先需要把t投影到格对应的扩展空间，形成点s；
2. 找到对应的数c，使得超平面尽可能接近点s；
3.  令。迭代去求，找点和格之间的关系，假定此时求得的答案为；
4. 最终返回的答案为；

第一步投影过程操作的目的是为了格点到t的最短距离，转化为到s的最短距离，此步的操作在非满秩格时非常有必要。往后的步骤就是每次选择最近的超平面，然后逐个维度去移动。