[密码学]格密码学（3）-Babai算法以及GGH公钥密码体制介绍

前两篇，我们介绍了同余公钥密码体制和背包公钥密码体制，接下来我们介绍下格的基本定义和性质。

1、格及SVP、CVP问题

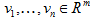
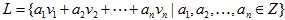
定义：线性独立空间上有集合，格（Lattices）就是这些向量的线性组合，用公式表示如下：。格L的维数等于格中向量的个数。

假定是格中格L的基，，则有必然存在 整系数使得：

，这样的话，格中的问题就是矩阵运算了。

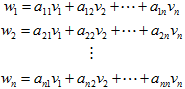
最短向量问题（SVP，The Shortest Vector Problem）：寻找一个格L中最短的非零向量。即，寻找一个满足其欧几里德范数||v||最小。

最接近向量问题（CVP，The Closest Vector Problem）：对于一个非格L中的向量w，在格中寻找一个向量v，使得||w-v||最小。

CVP和SVP都是NP完备问题，因此求解起来十分困难，因此这2个问题都是可以作为密钥体制的基础的。

2、Babai最接近向量算法

我们从下面的例子来解释该算法。

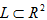
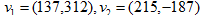
例1：设格，向量是格的基。去寻找一个一个L中的向量v满足||w-v||最小。其中w=(53172,81743)。

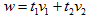
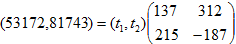
解：要寻找一个最近的向量，即，所以有下列的方程。

，可以解得到，，所以接近的向量为。

通过这个方法，我们求得了一个接近的向量，那么这样四舍五入产生的误差到底是有多大呢？

我们计算下||v-w||，其值大约为76.12，效果还是不错的，比较接近w了。

但是对于另一组基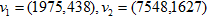，也是采用上面的办法，我们得到的v‘=(56405,82444)，计算||v'-w||=3308.12，误差较大。

对于两组基为什么会得到不太一样的效果呢？这里给大家介绍一下哈达马比例（Hadamard ratio）。

哈达马比例，（对于n维的情况下，有）对于上面的两组基，我们分别计算其哈达马比例。

（1）对于第一组基：

，十分接近于1。

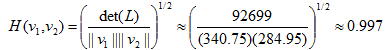
（2）对于第二组基：

，十分接近于0。

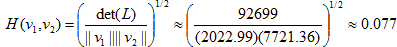
我们把接近于1的基称为好基（Good Basis），接近于0的基称为坏基（Bad Basis）。这里需要提的一点是，哈达马系数的范围是(0,1)的。

该题的解题想法，就是Babai算法的思想，找到一个好基，这样我们就可以近似的求出最接近的向量了。

Babai算法的java实现（用到jama包，可下载：http://math.nist.gov/javanumerics/jama/）。

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

import Jama.Matrix;

public class Babai {
	public static void main(String args[]) {
		// 输入维数
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		try {
			System.out.println("请输入格维数：");
			int N = Integer.parseInt(br.readLine());
			System.out.println("请输入格的基：");
			double[][] AMatrixArray = new double[N][N];
			for (int i = 0; i < N; i++) {
				for (int j = 0; j < N; j++) {
					AMatrixArray[i][j] = Integer.parseInt(br.readLine());
				}
			}
			Matrix AMatrix = new Matrix(AMatrixArray);
			// 输入需要计算的 向量
			double[][] vec = new double[1][N];
			for (int j = 0; j < N; j++) {
				vec[0][j] = Integer.parseInt(br.readLine());
			}
			Matrix b = new Matrix(vec);
			// 计算接近该向量的向量
			Matrix x = b.times(AMatrix.inverse());// 得到精确解
			double[][] appro = new double[1][N];
			for (int i = 0; i < N; i++) {
				appro[0][i] = x.get(0, i);
				if ((double) (x.get(0, i) - (int) appro[0][i]) > 0.5) {
					appro[0][i] = (int) appro[0][i] + 1.0;
				} else
					appro[0][i] = (int) appro[0][i] + 0.0;
			}
			Matrix ApproT = new Matrix(appro);
			Matrix ApproMatrixToVector = ApproT.times(AMatrix);
			// 分析误差以及其与基的Hadamard ratio of the basis
			// 计算相差距离
			double distance = 0;
			for (int i = 0; i < N; i++) {
				distance += Math.pow(
						(ApproMatrixToVector.get(0, i) - b.get(0, i)), 2);
			}
			distance = Math.pow(distance, 0.5);
			System.out.println("由这个基算的的误差为：" + distance);
			// 计算Hadamard ratio of the basis
			double mul =1;
			for(int i=0;i<N;i++)
			{
				double temp=0;
				for(int j =0;j<N;j++){
				temp+=Math.pow(AMatrix.get(i, j),2);
				}
				mul*=Math.pow(temp, 0.5);
			}
			 double HadamardRatio=Math.pow(Math.abs(AMatrix.det()/mul), 0.5);
			 System.out.println("您所输入的基的Hadamard比例为："+HadamardRatio);
		} catch (IOException e) {
			e.printStackTrace();
		}
	}
}

3、GGH公钥密码体制

首先给出该公钥密码体制的一个描述。如下：

（1）Alice公钥产生：选择一个好基，以及一个整数矩阵U，满足。计算W=UV，这样，我们得到一组坏基。即为我们的公钥。

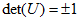
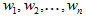
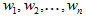
（2）加密：选择小明文向量m。选择随机小向量r。用Alice的公钥计算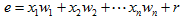。e就是密文。

（3）解密：用Babai算法计算最近向量v最接近e，再次计算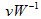即得到明文m。

该算法在此不给于实现了，有兴趣的读者可以自行实现一遍。

笔者水平有限，欢迎批评指正。