数字图像处理-频率域滤波原理

写在前面的话

作者是一名在读的硕士研究僧，方向是图像处理。由于图像处理是一门相对复杂的学科，作者在课堂上学到的东西只是非常浅显的内容，我们老师说是，领我们进了个门。现在打算利用图书馆和网络上的资源进行自学。由于是刚开始写自己的博客，并且所具备的专业知识非常的有限，难免有出错之处，如果有朋友发现一些毛病，希望能够指正。哈哈，话不多说，进入正题。
作者使用的是冈萨雷斯的《数字图像处理（Matlab版）》，打算先用matlab先跟着书上的内容把代码先练一练。以后，再重新学习深入一些的知识。这里不会将书中的全部内容都列一遍，我会选择性的把重要的部分代实现。

频率域

在介绍频率域图像处理之前，先提几个问题。
1.什么是频率域？
2.为什么要在频率域中进行图像处理？

频率域的概念
频率域是指从函数的频率角度出发分析函数，和频率域相对的是时间域。简单说就是如果从时间域分析信号时，时间是横坐标，振幅是纵坐标。而在频率域分析的时候则是频率是横坐标，振幅是纵坐标。
举个例子，我们认为音乐是一个随着时间变化的震动。但是如果站在频域的角度上来讲，音乐是一个随着频率变化的震动，这样我们站在时间域的角度去观察你会发现音乐是静止的。同理，如果我们站在时间域的角度观察频率域的世界，就会发现世界是静止的，也是永恒的。这是因为在频率域是没有时间的概念的，那么也就没有了随着时间变化着的世界了。
另外，我们需要借助傅立叶变换，才能够在得到函数在频率域中的信息。

为什么要在频率域中进行图像处理？
1). 可以利用频率成分和图像外表之间的对应关系。一些在空间域表述困难的增强任务，在频率域中变得非常普通；
2). 滤波在频率域更为直观，它可以解释空间域滤波的某些性质；
3).可以在频率域指定滤波器，做反变换，然后在空间域使用结果滤波器作为空间域滤波器的指导

傅里叶变换

谈到频率域，就不得不说傅里叶变换了。傅里叶是18世纪法国的一位伟大的数学家。他最大的贡献在于指出任何周期函数都可以表示为不同频率的正弦和或者余弦和的形式，每个正弦或者余弦乘以不同的系数（也就是被大家所熟知的傅里叶级数）。无论函数有多复杂，只要它是周期性的，并且满足一定的数学条件，就一定可以用这样的正弦和或者余弦和的形式来表示。甚至在有些情况下，非周期函数也可以用正弦和或者余弦和的形式来表示。用傅里叶级数或变换表示的函数特征可以完全通过傅里叶反变换来重建，而不会丢失任何信息。而正是所谓的“傅里叶变换”使得我们可以工作于频率域。

一维连续函数的fourier变换

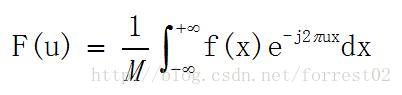
其中，f(x)表示原函数，F（u）表示变换之后的函数。u为频率域变量。