Is Fibonacci Search really "faster" than Binary Search?
申明:本文讨论的搜索对象为有序数组,不是数学上讨论的函数。
1. 介绍
对经过各种Sort算法排好序之后的有序数组进行检索的Search算法大致有以下三种:线性查找 O(n),二分查找 O(log(n)),斐波那契查找 O(log(n))。
前两者用的比较多,对于 Fibonacci Search,应该蛮多人和我一样只闻其名,不见其人吧。
数学原理如下:
斐波那契数列:0、1、1、2、3、5、8、13、21、……(有人喜欢从1开始,随你~~~)
如果设F(n)为该数列的第n项(n∈N)。那么这句话可以写成如下形式:
F(0) = 0,F(1)=1,F(n)=F(n-1)+F(n-2) (n≥2),显然这是一个线性递推数列,随着数列项数的增加,前一项与后一项之比越来越逼近黄金分割的数值0.6180339887..…
且看通项公式:
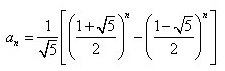
算法描述如下:
The Fibonacci Search Algorithm
Let Fk represent the k-th Fibonacci number where Fk+2=Fk+1 + Fk for k>=0 and F0 = 0, F1 = 1. To test whether an item is in a list of n = Fm ordered numbers, proceed as follows:
- Set k = m.
- If k = 0, finish - no match.
- Test item against entry in position Fk-1.
- If match, finish.
- If item is less than entry Fk-1, discard entries from positions Fk-1 + 1 to n. Set k = k - 1 and go to 2.
- If item is greater than entry Fk-1, discard entries from positions 1 to Fk-1. Renumber remaining entries from 1 to Fk-2, set k = k - 2 and go to 2.
If n is not a Fibonacci number, then let Fm be the smallest such number >n, augment the original array with Fm-n numbers larger than the sought item and apply the above algorithm for n'=Fm.
2.实验
实验数据:产生有序数组
|
1
2 3 4 5 6 |
#define NUM
4
int *array = ( int *)calloc(NUM, sizeof( int)); for ( int i = 0; i < NUM; ++i) { array[i] = i; } |
实验方法:三种搜索算法函数原型pData-数组,n-数组个数,key-待搜索关键字
|
1
2 3 4 |
int LineSearch(
int *pData,
int n,
int key);
int BinarySearch( int *pData, int n, int key); int FibonacciSearch( int *pData, int n, int key); |
方法实现:
线性查找
|
1
2 3 4 5 6 7 8 9 10 11 |
int LineSearch(
int *pData,
int n,
int key)
{ int idx = 0; while(idx != n ) { if(pData[idx] != key) idx++; else return idx; } } |
二分查找
|
1
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
int BinarySearch(
int *pData,
int n,
int key)
{ int center, left = 0, right = n - 1; while(left <= right) { center = (left + right) / 2; if (pData[center] > key) { right = center - 1; } else { if (pData[center] < key) left = center + 1; else return center; } } return - 1; } |
斐波那契查找
|
1
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 |
/* Fibonaccian search for locating the index of "key" in an array "pData" of size "n" that is sorted in ascending order. See http://doi.acm.org/10.1145/367487.367496 Algorithm description ----------------------------------------------------------------------------- Let Fk represent the k-th Fibonacci number where Fk+2=Fk+1 + Fk for k>=0 and F0 = 0, F1 = 1. To test whether an item is in a list of n = Fm ordered numbers, proceed as follows: a) Set k = m. b) If k = 0, finish - no match. c) Test item against entry in position Fk-1. d) If match, finish. e) If item is less than entry Fk-1, discard entries from positions Fk-1 + 1 to n. Set k = k - 1 and go to b). f) If item is greater than entry Fk-1, discard entries from positions 1 to Fk-1. Renumber remaining entries from 1 to Fk-2, set k = k - 2 and go to b) If Fm>n then the original array is augmented with Fm-n numbers larger than key and the above algorithm is applied. */ int FibonacciSearch( int *pData, int n, int key) { register int k, idx, offs; static int prevn = - 1, prevk = - 1; /* Precomputed Fibonacci numbers F0 up to F46. This implementation assumes that the size n * of the input array fits in 4 bytes. Note that F46=1836311903 is the largest Fibonacci * number that is less or equal to the 4-byte INT_MAX (=2147483647). The next Fibonacci * number, i.e. F47, is 2971215073 and is larger than INT_MAX, implying that it does not * fit in a 4 byte integer. Note also that the last array element is INT_MAX rather than * F47. This ensures correct operation for n>F46. */ const static int Fib[ 47 + 1] = { 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, 1346269, 2178309, 3524578, 5702887, 9227465, 14930352, 24157817, 39088169, 63245986, 102334155, 165580141, 267914296, 433494437, 701408733, 1134903170, 1836311903, INT_MAX }; /* find the smallest fibonacci number that is greater or equal to n. Store this * number to avoid recomputing it in the case of repetitive searches with identical n. */ if(n != prevn) { register int f0, f1, t; for(f0 = 0, f1 = 1, k = 1; f1 < n; t = f1, f1 += f0, f0 = t, ++k); prevk = k; prevn = n; } else k = prevk; /* If the sought value is larger than the largest Fibonacci number less than n, * care must be taken top ensure that we do not attempt to read beyond the end * of the array. If we do need to do this, we pretend that the array is padded * with elements larger than the sought value. */ for(offs = 0; k > 0; ) { idx = offs + Fib[--k]; /* note that at this point k has already been decremented once */ if(idx >= n || key < pData[idx]) // index out of bounds or key in 1st part { continue; } else if (key > pData[idx]) { // key in 2nd part offs = idx; --k; } else // key==pData[idx], found return idx; } return - 1; // not found } |
算法正确性验证:
C++ Code
|
1
2 3 |
printf(
"LineSearch Index : %d\n", LineSearch(array, NUM, array[
3]));
printf( "BinarySearch Index : %d\n", BinarySearch(array, NUM, array[ 3])); printf( "FibonacciSearch Index : %d\n", FibonacciSearch(array, NUM, array[ 3])); |
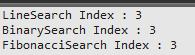
分析:
| (NUM=4) | 0 | 1 | 2 | 3 | total |
| Line | 0 | 1 | 2 | 3 | 7 |
| Binary | 1 | 0 | 1 | 2 | 4 |
| Fibonacci | 4 | 2 | 1 | 0 | 7 |
ps:第一行为待查找的关键值,本文将遍历序数组中的每个关键值的查找次数并相加(如果要表征平均,除以NUM即可,因为一样,所以就不除了),来表征平均搜索效率,因为当假设每个值被查找的概率相同,即符合均匀分布,还是有一定的合理性的。即total值越小,对单个关键值的搜索次数约有效率。
算法性能实验:
| NUM | 4 | 4E1 | 4E2 | 4E3 | 4E4 | 4E5 | 4E6 | 4E7 |
| Line | 6 | 780 | 79800 | 7998000 | 79998000 | - | - | - |
| Binary | 4 | 143 | 2687 | 39917 | 534481 | 6675732 (0.07s) | 79805719 (0.81s) | 932891163 (20.34s) |
| Fibonacci | 7 | 179 | 3189 | 42428 | 572324 | 7206170 (0.06s) | 86747879 (0.77s) | 1012299070 (12.31s) |
得到次数需要改写一些代码,改写的整个代码放在最后附录,需要的自己去验证下。
结论: 与二分查找相比,斐波那契查找的明显优点在于它只涉及加法和减法运算,而不用除法(可能用“>>1”要好点)。因为除法比加减法要占去更多的机时,因此,斐波那契查找的运行时间比二分查找短。 但前者的O(log(n))还是后者的大点,对某一个对象的平均搜索次数要小。所以,要取决于你如何看待“faster”了。
Reference:
附录:
Search.h
|
1
2 3 4 5 6 7 8 9 10 11 |
#include <stdio.h>
#include <stdlib.h> #include <limits.h> #include <time.h> #define NUM 4 int LineSearch( int* pData, int n, int key); int BinarySearch( int* pData, int n, int key); int FibonacciSearch( int* pData, int n, int key); |
Search.c
|
1
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 |
#include
"search.h"
//四种搜索算法 搜索遍历 有序数组所用的总次数 int main( int argc, char const *argv[]) { clock_t start, finish; double time_duration; //产生有序数组 int *array = ( int *)calloc(NUM, sizeof( int)); for ( int i = 0; i < NUM; ++i) { array[i] = i; } start = clock(); int tTmp; //线性查找 tTmp = 0; for ( int i = 0; i < NUM; ++i) { tTmp += LineSearch(array, NUM, array[i]); } printf( "LineSearch Index : %d\n", tTmp); //二分查找 tTmp = 0; for ( int i = 0; i < NUM; ++i) { tTmp += BinarySearch(array, NUM, array[i]); } printf( "BinarySearch Index : %d\n", tTmp); //斐波那契查找 tTmp = 0; for ( int i = 0; i < NUM; ++i) { tTmp += FibonacciSearch(array, NUM, array[i]); } printf( "FibonacciSearch Index : %d\n", tTmp); free(array); finish = clock(); time_duration = ( double)(finish - start) / CLOCKS_PER_SEC; printf( "Times Cost : %.2f \n", time_duration ); return 0; } int LineSearch( int *pData, int n, int key) { int idx = 0; int times = 0; while(idx != n ) { if(pData[idx] != key) times++, idx++; else return times; } return - 1; } int BinarySearch( int *pData, int n, int key) { int center, left = 0, right = n - 1; int times = 0; while(left <= right) { center = (left + right) / 2; if (pData[center] > key) { times++, right = center - 1; } else { if (pData[center] < key) times++, left = center + 1; else return times; } } return - 1; } /* Fibonaccian search for locating the index of "key" in an array "pData" of size "n" that is sorted in ascending order. See http://doi.acm.org/10.1145/367487.367496 Algorithm description ----------------------------------------------------------------------------- Let Fk represent the k-th Fibonacci number where Fk+2=Fk+1 + Fk for k>=0 and F0 = 0, F1 = 1. To test whether an item is in a list of n = Fm ordered numbers, proceed as follows: a) Set k = m. b) If k = 0, finish - no match. c) Test item against entry in position Fk-1. d) If match, finish. e) If item is less than entry Fk-1, discard entries from positions Fk-1 + 1 to n. Set k = k - 1 and go to b). f) If item is greater than entry Fk-1, discard entries from positions 1 to Fk-1. Renumber remaining entries from 1 to Fk-2, set k = k - 2 and go to b) If Fm>n then the original array is augmented with Fm-n numbers larger than key and the above algorithm is applied. */ int FibonacciSearch( int *pData, int n, int key) { register int k, idx, offs; static int prevn = - 1, prevk = - 1; int times = 0; /* Precomputed Fibonacci numbers F0 up to F46. This implementation assumes that the size n * of the input array fits in 4 bytes. Note that F46=1836311903 is the largest Fibonacci * number that is less or equal to the 4-byte INT_MAX (=2147483647). The next Fibonacci * number, i.e. F47, is 2971215073 and is larger than INT_MAX, implying that it does not * fit in a 4 byte integer. Note also that the last array element is INT_MAX rather than * F47. This ensures correct operation for n>F46. */ const static int Fib[ 47 + 1] = { 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, 1346269, 2178309, 3524578, 5702887, 9227465, 14930352, 24157817, 39088169, 63245986, 102334155, 165580141, 267914296, 433494437, 701408733, 1134903170, 1836311903, INT_MAX }; /* find the smallest fibonacci number that is greater or equal to n. Store this * number to avoid recomputing it in the case of repetitive searches with identical n. */ if(n != prevn) { register int f0, f1, t; for(f0 = 0, f1 = 1, k = 1; f1 < n; t = f1, f1 += f0, f0 = t, ++k); prevk = k; prevn = n; } else k = prevk; /* If the sought value is larger than the largest Fibonacci number less than n, * care must be taken top ensure that we do not attempt to read beyond the end * of the array. If we do need to do this, we pretend that the array is padded * with elements larger than the sought value. */ for(offs = 0; k > 0; ) { idx = offs + Fib[--k]; /* note that at this point k has already been decremented once */ if(idx >= n || key < pData[idx]) // index out of bounds or key in 1st part { times++; continue; } else if (key > pData[idx]) { // key in 2nd part times++; offs = idx; --k; } else // key==pData[idx], found return times; } return - 1; // not found } |























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








