全网最清楚：基于Matlab两个时间序列之间的交叉小波相干性

置顶有梦想的Frank博士

已于 2024-08-11 21:44:53 修改

阅读量6.6k

点赞数 11

分类专栏：数据分析数据绘图文章标签： matlab 算法开发语言

于 2024-05-16 16:02:35 首次发布

本文链接：https://blog.csdn.net/frankgis/article/details/138963784

版权

数据分析同时被 2 个专栏收录

26 篇文章

订阅专栏

数据绘图

21 篇文章

订阅专栏

文章目录

前言
小波相干的基本原理
使用步骤
出图效果
参考文献

前言

在MATLAB中实现小波相干（Wavelet Coherence）是一种强大的频域分析技术，可以帮助我们理解时间序列数据之间的相互关系，揭示不同频率下的相关性和变化趋势。本文将介绍小波相干的基本原理、在MATLAB中的实现步骤以及示例代码，帮助读者掌握这一重要的数据分析工具。
在这里插入图片描述

小波相干的基本原理

小波相干是一种衡量两个时间序列在频域上的相关性的方法。它通过计算小波变换后的信号之间的相干度来揭示它们之间的频域联系。与传统的相关性分析相比，小波相干能够提供更多关于信号频率和时变性的信息，因此在分析非平稳信号和多尺度数据时具有明显优势。与相关性类似，都是衡量两个变量之间的相关程度。相干性多用于频域计算，可以在基于频率上给出更多的信息，如相位信息。
基本步骤如下：

小波变换：首先对要分析的两个时间序列进行小波变换，将它们转换到小波域。小波变换具有多尺度和局部化特性，适用于分析非平稳信号的频率特征。
计算相干度：在小波域内，计算两个信号的小波相干度，即相干函数。它表示了两个信号在不同频率下的相关性程度，可以揭示信号之间的频域联系和时域相关性。
确定显著性：根据计算得到的小波相干度，可以进行显著性检验，确定哪些频率下两个信号之间存在显著的相互关系。

小波分析可以广泛运用于以下这些领域
信号处理：小波相干广泛用于处理非平稳信号，如生物医学信号、地震信号等，能够帮助提取有用的频率信息和时变特征。
气象学：在气象学中，小波相干可用于分析天气现象之间的关联，如降水和温度的关系，有助于预测气候变化和极端天气事件。
金融分析：小波相干也被应用于金融领域，用于分析股票价格、汇率等时间序列数据之间的相关性和周期性变化，辅助决策和风险管理。
地球科学：在地球科学领域，小波相干可用于研究地震、气候变化、海洋波浪等现象，揭示不同尺度下的地球系统动态变化。
水文学：小波分析在水文水资源系统中的应用研究包括捕捉大坝或水库的影响，揭示不同时频尺度下的水文情势的改变度。

使用步骤

步骤一：加载处理好的数据
步骤二：小波变换
步骤三：计算小波相干度
步骤四：绘制小波相干图

rng default;
t = 0:0.001:2;
x = cos(2*pi*10*t).*(t>=0.5 & t<1.1)+ ...
cos(2*pi*50*t).*(t>= 0.2 & t< 1.4)+0.25*randn(size(t));
y = sin(2*pi*10*t).*(t>=0.6 & t<1.2)+...
sin(2*pi*50*t).*(t>= 0.4 & t<1.6)+ 0.35*randn(size(t));
subplot(2,1,1)
plot(t,x)
title('X')
subplot(2,1,2)
plot(t,y)
title('Y')
xlabel('Time (seconds)')
[wcoh,~,period,coi] = wcoherence(x,y,seconds(0.001));
figure
period = seconds(period);
coi = seconds(coi);
h = pcolor(t,log2(period),wcoh);
h.EdgeColor = 'none';
ax = gca;
ytick=round(pow2(ax.YTick),3);
ax.YTickLabel=ytick;
ax.XLabel.String='Time';
ax.YLabel.String='Period';
ax.Title.String = 'Wavelet Coherence';
hcol = colorbar;
hcol.Label.String = 'Magnitude-Squared Coherence';
hold on;
plot(ax,t,log2(coi),'w--','linewidth',2)
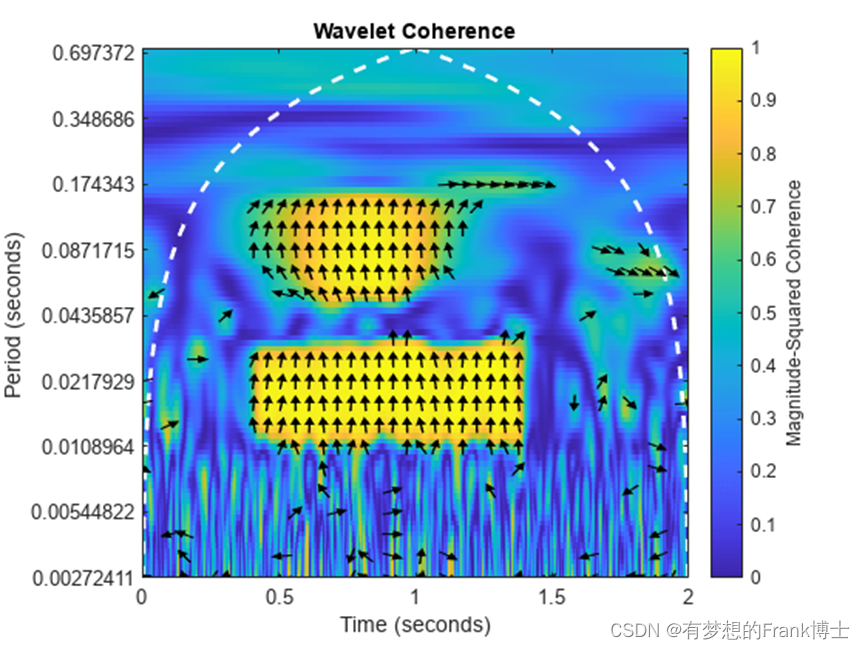
wcoherence(x,y);

出图效果

Zhao等人在2023年top期刊JOH上的研究中将小波相干方法用于探究水沙通量与降雨侵蚀力之间的关系：
在这里插入图片描述
Peng 等人2020年在Remote Sensing of Environment期刊上发表的研究中提出了一种基于小波相干分析的LST影响因素及其研究尺度的优选方法。解决了以下几个科学问题：（1）比较各影响因素与LST相干关系的多尺度稳定性；（2）确定各影响因素与LST具有显著相干关系的优先尺度；（3）根据与LST的稳定长尺度相干特征确定优先影响因素。
在这里插入图片描述
Cheng2022年总环期刊上的研究中将小波相干方法用于检测生态系统服务权衡对土地利用变化的响应。

在这里插入图片描述小波交叉谱:U型黑色细实线为小波边界效应影响锥(COI)，在该曲线以外的功率谱由于受到边界效应的影响而不子考虑; 黑色粗黑线包围的范围通过了0.05显著性水平下的红噪声标准谱的检验，箭头代表相位关系，其中←表示两个时序变量的变化位相相反，即两者呈负相关关系，→ 表示两者变化位相致，即两者呈正相关关系，↑表示指数A落后因子B变化1/4周期，↓表示指数A超前因子B变化1/4周期; 色柱表示能量密度的相对变化; XWT：交叉小波谱，WTC小波相干谱，以此类推。

欢迎关注我的公众号，博士期间日常科研分享，获取更多科研代码和前沿论文资讯等相关内容
若需要以上小波分析的代码，请关注公众号趣品科研回复“小波分析”关键词

参考文献

Peng J, Qiao R, Liu Y, et al. A wavelet coherence approach to prioritizing influencing factors of land surface temperature and associated research scales[J]. Remote Sensing of Environment, 2020, 246: 111866.
Zhao D, Xiong D, Zhang B, et al. Long-term response of runoff and sediment load to spatiotemporally varied rainfall in the Lhasa River basin, Tibetan Plateau[J]. Journal of Hydrology, 2023, 618: 129154.
Zhao R, Biswas A, Zhou Y, et al. Identifying localized and scale-specific multivariate controls of soil organic matter variations using multiple wavelet coherence (vol 643, pg 548, 2018) [J]. Science of the Total Environment, 2019(649-):649.
Cheng X, Xu Z, Yu S, et al. A wavelet coherence approach to detecting ecosystem services trade-off response to land use change[J]. Journal of environmental management, 2022, 316:115160.
He, K., Shi, H., Chen, C., Cheng, Y., & Liu, J. (2021). The study on the time lag of water level in the Three Gorges Reservoir under the regulation processes. Hydrology Research, 52, 734-748