脉冲神经网络介绍 STDP和Hebb

https://blog.csdn.net/Yannan_Strath/article/details/105761023
先贴一篇很好的介绍，本文有部分采用。

传统神经网络算法仍然依据于使用高精度的浮点数进行运算， 然而人脑并不会使用浮点数进行运算。 在人的传感系统和大脑中， 信息会以动作电压或称之为电脉冲（electric spike）的形式传递，接受，和处理。

那么，在SNN中， 信息是如何用spike来表达的呢？ 这就涉及到脉冲编码的知识了。 在SNN中， 很重要的一点是引入了时序（temporal）相关的处理形式。 信息是被编码在脉冲序列的时间序列（spike train）中的。
例如： 高频率的一组脉冲序列可以代表一个较高的值而低频率的脉冲则代表低值。
这种编码方式叫做频率编码（Rate coding），虽然效率不高，但是又很好的抗噪声能力。
频率编码又可以细分三种，
又例如： 在一个固定的时间窗中， 单个脉冲出现的位置也可以代表相应的值/信息，这种编码方式叫做时间编码（Temporal coding），好处是高效快速。

脉冲神经网络学习算法

脉冲神经网络常用无监督学习进行训练，有两种无监督学习的训练方法：
第一个就是Hebb学习率：
同步的突触前与突触后神经元电活动可造成突触加强或稳固
也就是突触前神经元的活动$y_i$和突触后神经元的活动$y_j$同号则突触$w_{ij}$变大，异号则变小，𝜂为训练速率。

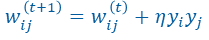
Hebb有一个变体Oja规则，再Hebb基础上加入了一项：

具体可以参考E. Oja, Simplied neuron model as a principal component analyzer, Journal of Mathematical Biology. 1982
这里重点介绍（STDP）突触可塑性机制这种无监督学习方法：
如果突触前放电先于突触后放电，叫LTP(长时程增强 long-term potentiation)，突触之间的连接权重应该加强，且时间间隔越小权重增加量越大，
$\Delta w_j=A_{+}{e}^{\frac{\Delta t_i}{{\tau }_{+}}}$
其中${\tau }_{+}$为时间常数，$A_{+}$为学习率，$\Delta t_i$为突触前脉冲传到突触后脉冲所需的时间，很明显此时$\Delta t_i<0$
如果突触后放电先于突触前放电，叫做LTD 长时程抑制 long-term depression，突触之间的连接权重应该减弱，且时间间隔越小权重减少量越大。
$\Delta w_j=-A_{-}{e}^{\frac{-\Delta t_i}{{\tau }_{-}}}$
上面提到的这种STDP叫做二相STDP。