先定义两个矩阵
a = [1 2 3 5 ; 4 7 9 5;1 4 6 7;5 4 3 7;8 7 5 1] %a矩阵取5*4
b = [1 5 4; 3 6 8; 1 5 7] %b矩阵如多数模板一样取3*3
那么conv(a,b)的结果肯定是(5+3-1)*(4+3-1)=7*6的矩阵
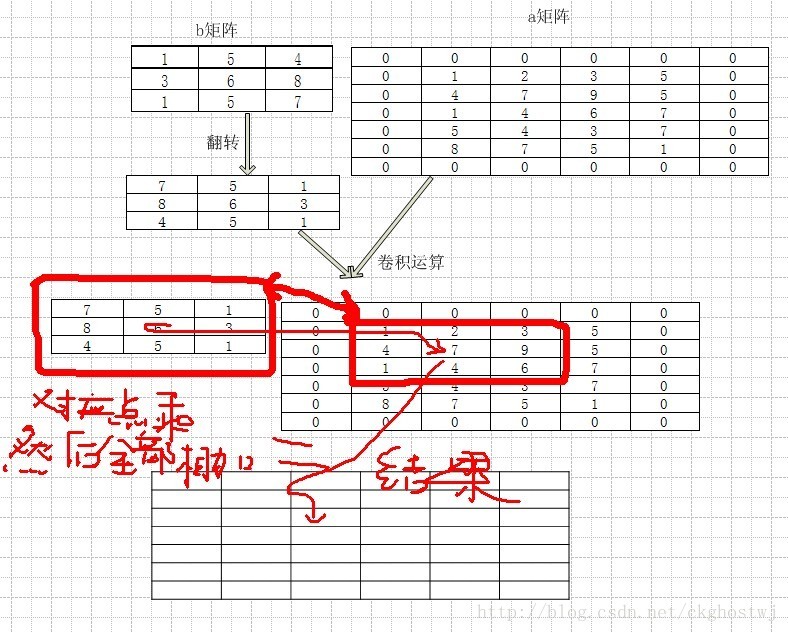
卷积计算过程如下:默认先把a矩阵补0变成7*6维的矩阵,然后b翻转 之后进行模板操作,要计算a矩阵中哪个点卷积以后的值,就把翻转之后b‘矩阵的中心如图中的6放到要计算的位子 然后对应的3*3矩阵对应位置相乘,之后全部相加即为对应点的卷积之后的结果。如下图所示
结果如下:
c=conv2(a,b)
c =
1 7 17 28 37 20
7 39 89 127 115 60
14 61 151 212 207 103
12 74 165 226 225 119
24 98 178 190 168 109
29 98 179 139 102 57
8 47 96 75 40 7
d=conv2(a,b,'same') %这个结果表示卷积出来的结果与a矩阵的维数一样
d =
39 89 127 115
61 151 212 207
74 165 226 225
98 178 190 168
98 179 139 102
接下来看看e=ifft2(fft2(a).*fft2(b));计算这个的时候由于是点乘,两个矩阵的维数应该相同因此首先应该将a、b两个矩阵都变成卷积之后的维数大小才行,这里都变成7*6维
因此首先:
a(7,6)=0;
b(7,6)=0;
此时a =
1 2 3 5 0 0
4 7 9 5 0 0
1 4 6 7 0 0
5 4 3 7 0 0
8 7 5 1 0 0
0 0 0 0 0 0
0 0 0 0 0 0
b =
1 5 4 0 0 0
3 6 8 0 0 0
1 5 7 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
然后执行e=ifft2(fft2(a).*fft2(b))
得到
e =
1.0000 7.0000 17.0000 28.0000 37.0000 20.0000
7.0000 39.0000 89.0000 127.0000 115.0000 60.0000
14.0000 61.0000 151.0000 212.0000 207.0000 103.0000
12.0000 74.0000 165.0000 226.0000 225.0000 119.0000
24.0000 98.0000 178.0000 190.0000 168.0000 109.0000
29.0000 98.0000 179.0000 139.0000 102.0000 57.0000
8.0000 47.0000 96.0000 75.0000 40.0000 7.0000
是不是与之前conv(a,b)的结果一样,只不过这里是双精度型的







 本文通过具体的矩阵示例,介绍了如何使用直接卷积和频域计算两种方法实现矩阵的卷积运算,并展示了两者结果的一致性。
本文通过具体的矩阵示例,介绍了如何使用直接卷积和频域计算两种方法实现矩阵的卷积运算,并展示了两者结果的一致性。
















 1452
1452

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








