http://blog.csdn.net/wangdingqiaoit/article/details/51383052
写在前面
前面几节内容环境搭建,绘制三角形,以及使用索引绘制,让我们对现代OpenGL中绘图做了简单了解。要继续后面的部分,需要熟悉OpenGL中涉及的数学知识。因此本节开始介绍OpenGL中的基本数学。
介绍这部分内容的主旨在于对OpenGL涉及的数学有个整体把握,重点把握一些概念在OpenGL中的应用。内容尽量以例子形式说明,仅在必要时会给出数学证明。一个主题往往涉及过多内容,对于文中省略的部分,请参考相应的教材。
通过本节可以了解到
- 向量基本概念和操作
- 矩阵的基本概念和操作
- GLM数学库
向量的概念
向量是研究2D、3D数学的标准工具。向量V是一个既有大小又有方向的量(联系位移和速度的概念)。在数学上,常用一条有方向的线段来表示向量。例如下图n维空间的向量
v=AB→=(v1,v2,...,vn)
如下图所示,向量起点为A,终点为B:
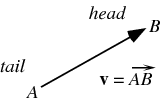
理解向量把握:
1.向量的大小就是向量的长度(模)。向量的长度非负。
2.向量的方向描述了向量的指向。
3.向量是没有位置的,与点是不同的。
4.向量与标量不同,变量是只有大小而没有方向的量,例如位移是向量,而距离是标量。
零向量与单位向量
向量的长度即模,定义为:
|v|=v21+v22+⋯+v2n−−−−−−−−−−−−−−√
即
|v|=∑ni=1v2i−−−−−−√
模等于0的向量成为0向量,模等于1的向量叫做单位向量。注意零向量的方向是任意的。
由一个向量v求与它同方向的单位向量过程称为标准化(normalization),这个单位向量成为标准化向量(normalized vector)。计算过程为:
vnorm=v|v|,v≠0
三角形法则和平行四边形法则
两个向量
a
和
b
,当将b的起点放在a的终点,连接a的起点和b的终点的向量成为向量
a
,
b
之和,记为:
c=a+b
,如下图所示(图片来自:mathinsight):
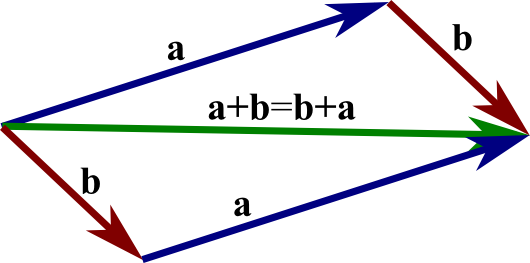
物理上力学求和经常使用平行四边形法则,表达的是向量加法运算的结合律,即:
a+b=b+a
,如下图所示(图片来自:mathinsight):
与一个向量
a
大小相同,方向相反的向量,称为向量
a
的负向量,两者相加得到零向量,即:
a+(−a)=0
向量夹角
两个非零向量的夹角规定为不超过
π
的角度
θ
,即
0≤θ≤π
如下图所示:
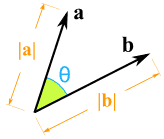
注意这个夹角的范围。当
θ=π2
称两个向量a与b垂直,当
θ=0或者π
时,称向量a与b平行。
向量点积(dot product)
向量点积,也称为向量的数量积,点积的结果是一个标量,其定义为:
A.B=|A||B|cosθ(1)
其中
θ
表示向量A和B之间的夹角。
向量点积的几何意义
要理解点积的几何意义,首先了解概念向量在轴上的投影(scalar projection ),这个投影计算得到一个标量。向量A在B上的投影定义为:
AB=|A|cosθ(2)
如下图所示(来自wiki dot product):
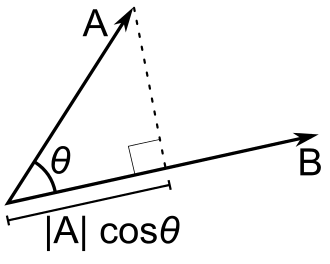
则1式可以写为:
A.B=|A|BA=|B|AB(3)
在空间几何中,例如n空间中,向量的坐标表示为:
A=(a1,b2,⋯,cn)
,
B=(b1,b2,⋯,bn)
,
则两个向量的点积可以表示为:
向量点积的应用
向量点积的一个重要应用在于,可以快速求出两个向量的夹角余弦。
由公式1可知,两个向量的夹角余弦计算公式为:
cosθ=a.b|a||b|(5)
当a和b都是单位向量时,两单位向量的夹角余弦值为:
cosθ=a.b(6)
公式6能快速计算出两个单位向量的夹角余弦,在计算光照时经常使用。
另外当一个向量为单位向量时:
|a|2=a⋅a(7)
这个公式也是经常使用的。
向量的叉积(cross product)
两个向量a和b的叉积,结果是一个向量
c=a×b
,c的方向垂直于a和b,它需要根据右手规则来确定(下文讲解);c的大小等于
|c|=|a||b|sinθ(8)
叉积如下图所示(来自wiki):
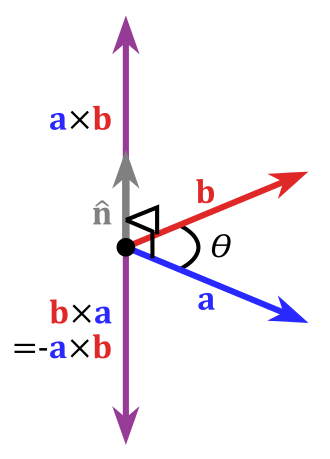
注意c的方向需要根据右手规则来确定。所谓右手规则是指,将向量a与b放在同一个起点时,当右手的四个手指从a所指方向转到b所指方向握拳时,大拇指的指向即为
a×b
的方向。如下图所示(来自cross product):
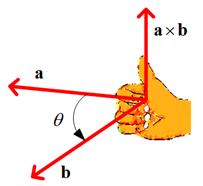
尤其要注意
a×b≠b×a
事实上,
a×b=−b×a(9)
在利用以坐标形式表示向量a和b时,在3D空间中,叉积的结果用矩阵表示为(矩阵下文介绍):
叉积的几何意义
叉积的模可以视为以a和b为两边的平行四边形的面积,如下图所示(来自 wiki):
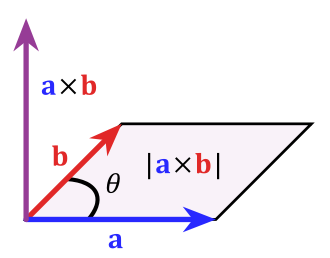
其中 |b|sinθ 可以视为平行四边形的高,计算后 a×b 的模即为平行四边形的面积。
叉积的应用
在OpenGL图形编程中,叉积经常在已知两个方向时,用来确定第三个方向。例如已知相机的朝向dir和侧向量side,则相机的顶部向量为: up=dir×side ,后面再介绍相机矩阵时会用到。
投影向量的计算
一个向量a在另一向量b上的投影向量,包括与b平行的部分
a1
和与b垂直的部分
a2
。
a1
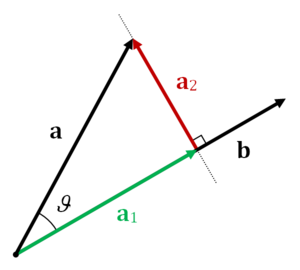
即是之前提到的scalar projection,不过这里
a1
是一个向量。具体过程如下图所示:
右图可知与b平行分量
a1
可计算为:
垂直分量 a2 计算为:
a2=a−a1=a−a⋅b|b|2b(12)
投影向量的应用
投影向量的计算过程,是一个向量分解的过程,这种向量分解的思路在后面推导其他内容时很有帮助,例如求解后面的物体旋转矩阵时会派上用场。
矩阵的概念
矩阵从形式上就是一个数字表,以行和列的形式呈现,简单的矩阵如下图所示:
⎡⎣⎢147258369⎤⎦⎥
矩阵的行数m和列数n可以不相同,m行n列矩阵记为矩阵
Am×n
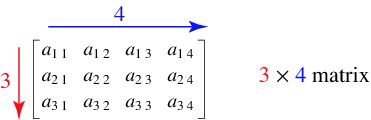
。当行数和列数相等时,m= n ,矩阵A也称为n阶方阵。例如下图给出了3x4矩阵
A3×4
的抽象表示:
行向量和列向量
对于1xn的矩阵,我们称之为行向量,nx1的矩阵称为列向量。一般可以用列向量表示空间中的向量(以行向量表示也可以),例如上面的向量
a=(ax,by,cz)
可以用列向量表示为:
a=⎡⎣⎢axayaz⎤⎦⎥
注意 OpenGL编程中习惯用列向量表示点或者向量。矩阵在内存中以列优先存储,但是具体传递参数时,一般函数提供了是否转置的布尔参数来调整存储格式。例如void glUniformMatrix4fv函数提供了布尔变量 GLboolean transpose 来表示是否转置矩阵。
零矩阵和n阶单位阵
mxn矩阵,如果所有元素都为0,则成为零矩阵。
对于一个n阶方阵,如果主对角线元素全为1,其余元素都为0则称为n阶单位阵。对于一个矩阵
Am×n
,存在单位阵满足:
ImA=AIn=A
.
任意矩阵
Am×n
与对应的零矩阵
Bn×p
相乘得到零矩阵。
矩阵转置
转置操作即是将矩阵的行和列互换,即原矩阵
A
的第一行变为转置矩阵
AT
的第一列,原矩阵
A
的第二行变为转置矩阵
AT
的第二列,其他部分依次类推。
例如矩阵
则其转置矩阵为:
矩阵的运算
矩阵加减法
两个矩阵A和B要能执行加减法,必须是行和列数目相等的,计算过程,即对应的元素相加(
Aij+Bij
)或者相减(
Aij−Bij
),如下图所示:
标量和矩阵乘法
用一个数k乘以矩阵A,结果为矩阵A中每个元素乘以数k。例如:
矩阵和矩阵乘法
两个矩阵
Am×n
和
Bn×p
要执行乘法操作,需要满足: 左边矩阵的列数和右边矩阵的行数相等,并且结果矩阵为
Cm×p
。
计算过程如下图所示(来自:mathworld):
其中
Cij=∑nk=1aikbkj
,即C中第i行第j列的元素,即为矩阵A的第i行和第j的对应元素相乘后的和。例如
注意矩阵乘法不满足交换律 一般而言矩阵乘积 AB≠BA (当然存在特殊情况下满足),因此在OpenGL中应用变换矩阵时注意变换应用的顺序。变换的例子后面会介绍。
矩阵和矩阵相乘举例
给定两个矩阵相乘,过程如下图所示(来自:mathsisfun):
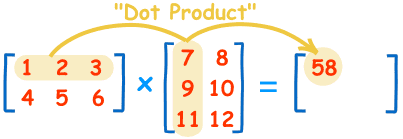
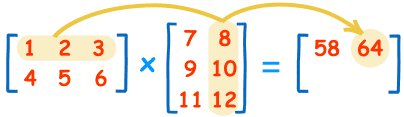
熟悉了矩阵相乘后,则上述向量的点积公式可以重新表示为:
a=(a1,b2,⋯,cn)
,
b=(b1,b2,⋯,bn)
,
则两个向量的点积可以表示为:
矩阵不满足交换律举例
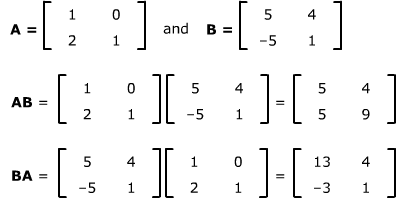
这里
AB≠BA
,提醒我们注意矩阵相乘时的顺序。
矩阵和向量相乘
矩阵和向量相乘是矩阵和矩阵相乘的特例,给定矩阵A和列向量v,相乘过程如下所示(来自mathinsight):
行列式
行列式是n阶方阵的数字构成的数的行列集合,例如2阶方阵A表示为:
A=[acbd]
其行列式det(A)表示为:
3x3矩阵的行列式计算如下:
关于矩阵行列式计算的更多方法可以参考线性代数教材。
逆矩阵
对于n阶方阵A,如果存在一个n阶方阵B使得:
AB=BA=I(14)
成立,则称B是A的逆矩阵,这时就说矩阵A是可逆矩阵,或者说矩阵A时非奇异矩阵(Nonsingular matrix)。单位矩阵
I
是主对角线上元素为1,其余元素都为0的n阶方阵。例如3x3的单位矩阵为:
I3x3=⎡⎣⎢100010001⎤⎦⎥
注意 只有n阶方阵才有逆矩阵的概念,对于一般的矩阵
Am×n(m≠n)
不存在这样的矩阵B满足14式。
n阶方阵A可逆的充要条件是A的行列式
|A|≠0
.
逆矩阵的应用意义
在3D图形处理中,用一个变换矩阵乘以向量,代表了对原始图形进行了某种变换,例如缩小,旋转等,逆矩阵表示这个操作的逆操作,也就是能够撤销这一操作。例如对一个向量v用矩阵M相乘,然后再用
M−1
相乘,则能得到原来的向量v:
M−1(Mv)=(M−1M)v=Iv=v
注意转换矩阵应用顺序 当用矩阵A,B,C转换向量v时,如果v用行向量记法,则矩阵按转换顺序从左往右列出,表达为 vABC ;如果v采用列向量记法,则转换矩阵应该放在左边,并且转换从右往左发生,对应的转换记为 CBAv 。
正交矩阵
对于方阵M,当且仅当M与其转置矩阵
MT
的乘积等于单位矩阵时,称其为正交矩阵。即:
M正交⇔MMT=I⇔MT=M−1(15)
正交矩阵的一大优势在于,计算逆矩阵时,只需要对原矩阵转置即可,从而减少了计算量。在3D图形处理中的旋转和镜像变换都是正交的。
对于n阶方阵A,它是正交矩阵的重要条件是A的行向量为一个相互正交的单位向量组,即
A=⎡⎣⎢⎢⎢⎢β1β2⋮βn⎤⎦⎥⎥⎥⎥
为正交矩阵的充要条件是:
An×n正交⇔βiβTj={1,0,i=ji≠j(16)
注意这里
βi
表示的是行向量。上述条件可以叙述为:
- 矩阵的每一行都是单位向量
- 矩阵的所有行互相垂直。
这个重要条件可以利用 MMT=I 加以证明。利用这个充要条件可以作为快速判断一个矩阵 M 是否是正交矩阵的方法。对于矩阵的列也可以得到类似的条件。同时也可以得到,如果 M 是正交矩阵,则 MT 也是正交矩阵。
正交矩阵举例
例如下面的矩阵
Rx(θ)
表示物体绕x轴的旋转
θ
角度。
Rx(θ)=⎡⎣⎢⎢⎢10000cosθsinθ00−sinθcosθ00001⎤⎦⎥⎥⎥
可以验证矩阵的行向量都满足上面的条件16,则
Rx(θ)
为正交矩阵。
也可以通过旋转矩阵本身的特性证明。对于旋转而言,绕x轴旋转
θ
角度的逆操作等于绕x轴旋转
−θ
角度,因此有:
Rx(θ)−1=Rx(−θ)(*)
应用:
cos(−θ)=cosθ
和
sin(−θ)=−sinθ
得到:
Rx(−θ)=⎡⎣⎢⎢⎢10000cosθ−sinθ00sinθcosθ00001⎤⎦⎥⎥⎥
可以发现:
Rx(−θ)=Rx(θ)T(**)
由*和**式子得到:
Rx(θ)−1=Rx(θ)T(***)
由式15和***式得到 Rx(θ) 为正交矩阵。
GLM数学库中的向量和矩阵
GLM是一个C++编写的,基于OpenGL着色器语言规范编写只是用头文件的图形开发数学库。这个库中提供了我们需要的很多数学操作,例如包含本节提到的向量和矩阵。例如下面的代码是用了向量的标准化、叉积等操作求取了一个三角形的法向量:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
例如与4x4矩阵对应类为 glm::mat4,其他更多的操作可以查看其参考文档,具体使用方法在后面应用时再做介绍。下一节介绍理解坐标、线性变换、仿射变换以及坐标转换所需的数学基础。
参考资料
1.《3D数学基础:图形与游戏开发》清华大学出版社
2.《线性代数》武汉大学数学与统计学院 高等教育出版社 齐民友主编
3. 《交互式计算机图形学-基于OpenGL着色器的自动向下方法》电子工业出版社 Edward Angle等著









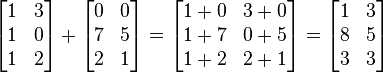
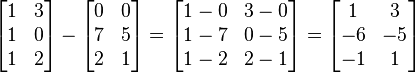
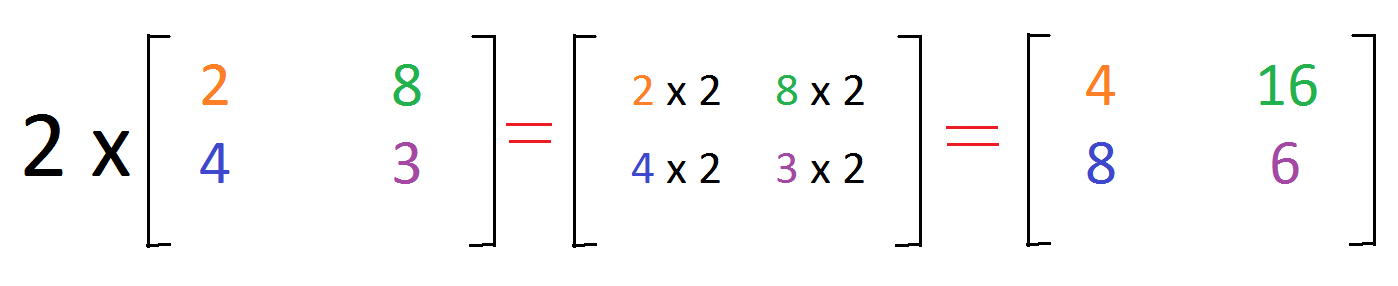
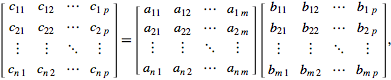
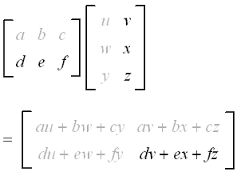
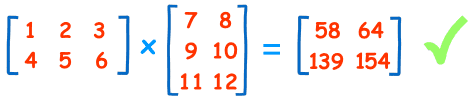














 1003
1003

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








