激活函数如何引入非线性

顺其自然~

已于 2024-04-23 14:35:12 修改

阅读量901

点赞数

文章标签：激活函数

于 2023-12-25 20:43:09 首次发布

原文链接：https://blog.csdn.net/weixin_39910711/article/details/114849349

版权

1、激活函数的概念和作用

1.1、激活函数的概念

激活函数（Activation Function）是一种添加到人工神经网络中的函数，旨在帮助网络学习数据中的复杂模式。类似于人类大脑中基于神经元的模型，激活函数最终决定了要发射给下一个神经元的内容。

在人工神经网络中，一个节点的激活函数定义了该节点在给定的输入或输入集合下的输出。标准的计算机芯片电路可以看作是根据输入得到开（1）或关（0）输出的数字电路激活函数。因此，激活函数是确定神经网络输出的数学方程式。

激活函数是人工神经网络中不可或缺的组成部分，它们负责将神经元的输入映射到输出端。以下是一些常见的激活函数及其特点：

1）Sigmoid函数：Sigmoid函数是一种广泛应用的激活函数，它将变量映射到0和1之间，形成S形曲线。它常用于二分类问题中，因为它的输出可以解释为概率。

2）Tanh函数：Tanh函数（双曲正切）与Sigmoid函数类似，但它将输出值域扩展到了-1到1之间。Tanh函数的中心点在零值附近，这意味着它的输出均值为0，这有助于梯度的收敛（在数学和经济学科中，收敛指的是一系列数值或函数向某个特定值靠近的过程）。

3）ReLU函数：ReLU（修正线性单元）激活函数是当前非常流行的一种激活函数，它的特点是简单且计算效率高效。ReLU函数会保留所有正数值不变，并将所有负数值设为零。这种特性使得ReLU能够有效地解决梯度消失问题，并加速神经网络的学习过程。

4）Leaky ReLU：为了解决ReLU函数在输入值为负时可能导致神经元“死亡”的问题，Leaky ReLU引入了一个小的斜率，允许负值有一个非零的梯度，这样即使输入值为负，神经元仍然可以学习。

此外，选择合适的激活函数对于网络的性能至关重要。不同的激活函数适用于不同类型的任务和网络架构。例如，Sigmoid和Tanh由于它们的平滑性和饱和性，可能在某些情况下导致梯度消失问题，而ReLU及其变体通常在这方面表现更好。

激活函数在神经网络中的名称来源于它们的作用，即“激活”或引入非线性因素，使得神经网络能够学习并拟合复杂的数据模式。以下是一些详细的解释：

1）非线性转换：激活函数对输入数据进行非线性转换，这是神经网络能够处理复杂任务的关键。如果没有非线性变换，神经网络将无法超越简单的线性模型，例如线性回归。

2）模拟神经元：神经网络的构建灵感来自于生物学中的神经元工作原理。激活函数在人工神经网络中的作用类似于生物神经元的激活过程，它决定了神经元是否应该被激活，以及激活的程度。

3）增加模型容量：通过使用激活函数，神经网络可以具有多个层次，每一层都可以捕捉数据的更复杂的特征。理论上，仅包含足够多神经元的两层网络就可以近似任何函数。

4）梯度和反向传播：激活函数的选择还影响了神经网络训练过程中的梯度计算和反向传播。合适的激活函数能够保证梯度不会在传播过程中消失或爆炸，从而帮助网络更好地学习和更新权重。

5）解决线性不可分问题：在面对线性不可分的问题时，如某些分类问题，单层感知机无法很好地完成任务。此时，引入激活函数的多层神经网络可以有效地解决问题，因为它们能够拟合更加复杂的决策边界。

综上所述，激活函数是神经网络的核心组成部分，它们通过引入非线性特性，使得神经网络能够学习和模拟各种复杂的数据关系。

首先我们来了解一下人工神经元的工作原理，大致如下：

上述过程的数学可视化过程如下图所示：

1.2、激活函数的作用

关于神经网络中的激活函数的作用，通常都是这样解释：不使用激活函数的话，神经网络的每层都只是做线性变换，多层输入叠加后也还是线性变换。因为线性模型的表达能力通常不够，所以这时候就体现了激活函数的作用了，激活函数可以引入非线性因素。疑问就来了，激活函数是如何引入非线性因素呢？

1.3、通俗的理解一下激活函数

为了解释激活函数如何引入非线性因素，接下来让我们以神经网络分割平面空间作为例子。

1.3.1、无激活函数的神经网络

神经网络最简单的结构就是单输出的单层感知机，单层感知机只有输入层和输出层，分别代表了神经感受器和神经中枢。下图是一个只有2个输入单元和1个输出单元的简单单层感知机。图中x1、x2代表神经网络的输入神经元受到的刺激，w1、w2代表输入神经元和输出神经元间连接的紧密程度，b代表输出神经元的兴奋阈值，y为输出神经元的输出。我们使用该单层感知机划出一条线将平面分割开，如图所示：

同理，我们也可以将多个感知机（注意，不是多层感知机）进行组合获得更强的平面分类能力，如图所示：

再看看包含一个隐层的多层感知机的情况，如图所示：

通过对比可以发现，上面三种没有激励函数的神经网络的输出都是线性方程，其都是在用复杂的线性组合来试图逼近曲线。

1.3.2、带激活函数的神经网络

让我们在神经网络每一层神经元做完线性变换以后，加上一个非线性激励函数对线性变换的结果进行转换，结果显而易见，输出立马变成一个不折不扣的非线性函数了，如图所示：

拓展到多层神经网络的情况，和刚刚一样的结构，加上非线性激励函数之后，输出就变成了一个复杂的非线性函数了，如图所示：

总结：加入非线性激励函数后，神经网络就有可能学习到平滑的曲线来分割平面，而不是用复杂的线性组合逼近平滑曲线来分割平面，使神经网络的表示能力更强了，能够更好的拟合目标函数。这就是为什么我们要有非线性的激活函数的原因。如下图所示说明加入非线性激活函数后的差异，上图为用线性组合逼近平滑曲线来分割平面，下图为平滑的曲线来分割平面：

2、神经网络梯度消失与梯度爆炸

2.1、简介梯度消失与梯度爆炸

层数比较多的神经网络模型在训练的时候会出现梯度消失(gradient vanishing problem)和梯度爆炸(gradient exploding problem)问题。梯度消失问题和梯度爆炸问题一般会随着网络层数的增加变得越来越明显。

例如，对于图1所示的含有3个隐藏层的神经网络，

梯度消失问题发生时，靠近输出层的hidden layer 3的权值更新相对正常，但是靠近输入层的hidden layer1的权值更新会变得很慢，导致靠近输入层的隐藏层权值几乎不变，仍接近于初始化的权值。这就导致hidden layer 1 相当于只是一个映射层，对所有的输入做了一个函数映射，这时此深度神经网络的学习就等价于只有后几层的隐藏层网络在学习。

梯度爆炸的情况是：当初始的权值过大，靠近输入层的hidden layer 1的权值变化比靠近输出层的hidden layer 3的权值变化更快，就会引起梯度爆炸的问题。

2.2、梯度不稳定问题

在深度神经网络中的梯度是不稳定的，在靠近输入层的隐藏层中或会消失，或会爆炸。这种不稳定性才是深度神经网络中基于梯度学习的根本问题。

梯度不稳定的原因：前面层上的梯度是来自后面层上梯度的乘积。当存在过多的层时，就会出现梯度不稳定场景，比如梯度消失和梯度爆炸。

2.3、产生梯度消失的根本原因

我们以图2的反向传播为例，假设每一层只有一个神经元且对于每一层都可以用公式1表示，其中σ为sigmoid函数，C表示的是代价函数，前一层的输出和后一层的输入关系如公式1所示。我们可以推导出公式2。

$z_i=w_ix_i+b_i$

$y_i=\sigma (z_i)=\sigma (w_ix_i+b_i)$ ，其中 $x_i=y_{i-1}$ （1)

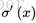
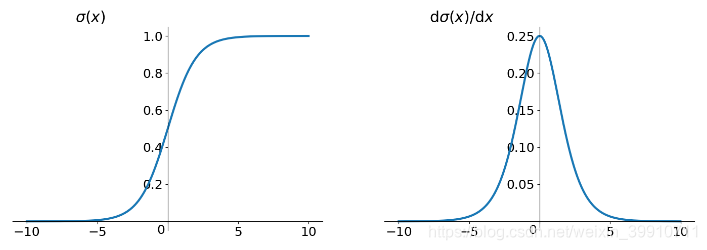
而sigmoid函数的导数如图3右图所示所示。

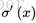
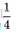
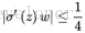
可见，的最大值为，而我们一般会使用标准方法来初始化网络权重，即使用一个均值为0标准差为1的高斯分布。因此，初始化的网络权值通常都小于1，从而有。对于2式的链式求导，层数越多，求导结果越小，最终导致梯度消失的情况出现。

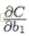
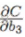
对于图4，和有共同的求导项。可以看出，前面的网络层比后面的网络层梯度变化更小，故权值变化缓慢，从而引起了梯度消失问题。

2.4、产生梯度爆炸的根本原因

当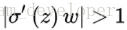，也就是w比较大的情况。则前面的网络层比后面的网络层梯度变化更快，引起了梯度爆炸的问题。

2.5、当激活函数为sigmoid时，梯度消失和梯度爆炸哪个更容易发生？

结论：梯度爆炸问题在使用sigmoid激活函数时，出现的情况较少，不容易发生。

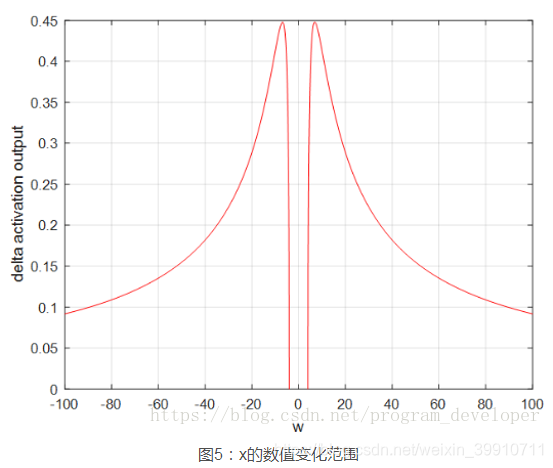
量化分析梯度爆炸时x的取值范围：因导数最大为0.25，故|w|>4，才可能出现；按照可计算出x的数值变化范围很窄，仅在公式3范围内，才会出现梯度爆炸。画图如5所示，可见x的数值变化范围很小；最大数值范围也仅仅0.45，当|w|=6.9时出现。因此仅仅在此很窄的范围内会出现梯度爆炸的问题。

2.6、如何解决梯度消失和梯度爆炸

梯度消失和梯度爆炸问题都是因为网络太深，网络权值更新不稳定造成的，本质上是因为梯度反向传播中的连乘效应。对于更普遍的梯度消失问题，可以考虑一下三种方案解决：

1）用ReLU、Leaky-ReLU、P-ReLU、R-ReLU、Maxout等替代sigmoid函数。

2）用Batch Normalization。

3）LSTM的结构设计也可以改善RNN中的梯度消失问题。

3、激活函数的比较

反之，不满足以上条件的函数则称为非饱和激活函数。

sigmoid和tanh是“饱和激活函数”，而ReLU及其变体则是“非饱和激活函数”。使用“非饱和激活函数”的优势在于两点：(1)"非饱和激活函数”能解决所谓的“梯度消失”问题。(2)它能加快收敛速度。

Sigmoid函数将一个实值输入压缩至[0,1]的范围---------σ(x) = 1 / (1 + exp(−x))

tanh函数将一个实值输入压缩至 [-1, 1]的范围---------tanh(x) = 2σ(2x) − 1

由于使用sigmoid激活函数会造成神经网络的梯度消失和梯度爆炸问题，所以许多人提出了一些改进的激活函数，如：tanh、ReLU、Leaky ReLU、PReLU、RReLU、ELU、Maxout。

3.1、Sigmoid

Sigmoid是常用的非线性的激活函数，它的数学形式如公式4：

上图左边为原函数，右边为导数（导函数）的图像。

特点：它能够把输入的连续实值变换为0和1之间的输出，特别的，如果是非常大的负数，那么输出就是0；如果是非常大的正数，输出就是1。

Sigmoid函数是深度学习领域开始时使用频率最高的activation function。它是便于求导的平滑函数，其导数为，这是优点。

在什么情况下适合使用 Sigmoid 激活函数？

1）Sigmoid 函数的输出范围是 0 到 1。由于输出值限定在 0 到 1，因此它对每个神经元的输出进行了归一化；

2）用于将预测概率作为输出的模型。由于概率的取值范围是 0 到 1，因此 Sigmoid 函数非常合适；

3）梯度平滑，避免「跳跃」的输出值；

4）函数是可微的。这意味着可以找到任意两个点的 sigmoid 曲线的斜率；

5）明确的预测，即非常接近 1 或 0。

缺点

1）容易出现gradient vanishing梯度消失

2）函数输出并不是zero-centered

3）幂运算相对来讲比较耗时

（1）Gradient Vanishing

优化神经网络的方法是Back Propagation，即导数的后向传递：先计算输出层对应的 loss，然后将 loss 以导数的形式不断向上一层网络传递，修正相应的参数，达到降低loss的目的。 Sigmoid函数在深度网络中常常会导致导数逐渐变为0，使得参数无法被更新，神经网络无法被优化。原因在于两点：

1）在上图中容易看出，当中较大或较小时，导数接近0，而后向传递的数学依据是微积分求导的链式法则，当前层的导数需要之前各层导数的乘积，几个小数的相乘，结果会很接近0。

2）Sigmoid导数的最大值是0.25，这意味着导数在每一层至少会被压缩为原来的1/4，通过两层后被变为1/16，…，通过10层后为1/1048576。请注意这里是“至少”，导数达到最大值这种情况还是很少见的。

（2）输出不是zero-centered

Sigmoid函数的输出值恒大于0，这会导致模型训练的收敛速度变慢。举例来讲，对，如果所有均为正数或负数，那么其对的导数总是正数或负数，这会导致如下图红色箭头所示的阶梯式更新，这显然并非一个好的优化路径。深度学习往往需要大量时间来处理大量数据，模型的收敛速度是尤为重要的。所以，总体上来讲，训练深度学习网络尽量使用zero-centered数据 (可以经过数据预处理实现) 和zero-centered输出。

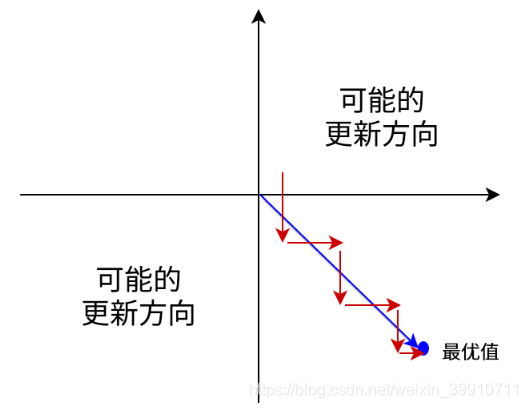
不是zero-centered产生的一个结果就是：如果数据进入神经元的时候是正的，那么 w 计算出的梯度也会始终都是正的。当然了，如果你是按batch去训练，那么那个batch可能得到不同的信号，所以这个问题还是可以缓解一下的。因此，非0均值这个问题虽然会产生一些不好的影响，不过跟上面提到的 kill gradients 问题相比还是要好很多的。

（3）幂运算相对耗时

相对于前两项，这其实并不是一个大问题，我们目前是具备相应计算能力的，但面对深度学习中庞大的计算量，最好是能省则省。之后我们会看到，在ReLU函数中，需要做的仅仅是一个thresholding，相对于幂运算来讲会快很多。

3.2、tanh函数

tanh 激活函数的图像也是 S 形，表达式如下：

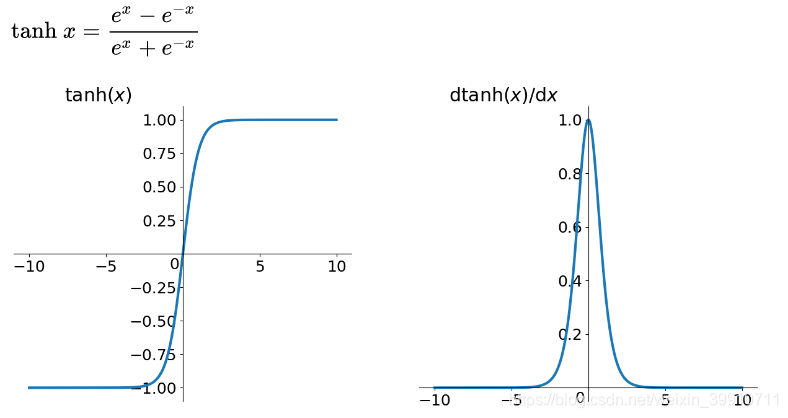
tanh读作Hyperbolic Tangent，如上图所示，它解决了zero-centered的输出问题，然而，gradient vanishing的问题和幂运算的问题仍然存在。

tanh 是一个双曲正切函数。tanh 函数和 sigmoid 函数的曲线相对相似。但是它比 sigmoid 函数更有一些优势。

首先，当输入较大或较小时，输出几乎是平滑的并且梯度较小，这不利于权重更新。二者的区别在于输出间隔，tanh 的输出间隔为 1，并且整个函数以 0 为中心，比 sigmoid 函数更好；

在 tanh 图中，负输入将被强映射为负，而零输入被映射为接近零。

注意：在一般的二元分类问题中，tanh 函数用于隐藏层，而 sigmoid 函数用于输出层，但这并不是固定的，需要根据特定问题进行调整。

3.3、ReLU

近年来，ReLU函数变得越来越受欢迎。全称是Rectified Linear Unit，中文名字：修正线性单元（是线性单元，但是是经过修正的，不是纯线性单元）。ReLU是Krizhevsky、Hinton等人在2012年《ImageNet Classification with Deep Convolutional Neural Networks》论文中提出的一种线性且不饱和的激活函数。它的数学表达式：

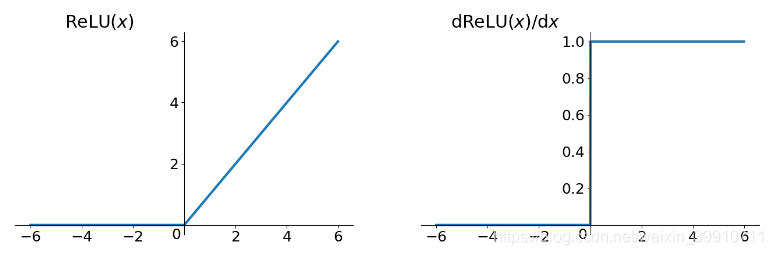
ReLU函数其实就是一个取最大值函数，注意这并不是全区间可导的，但是我们可以取sub-gradient，如上图所示。ReLU虽然简单，但却是近几年的重要成果，有以下几大优点：

1）解决了gradient vanishing问题 (在正区间)

2）Sigmoid和Tanh激活函数均需要计算指数，复杂度高，而ReLU只需要一个阈值即可得到激活值。ReLU 函数中只存在线性关系，因此它的计算速度比 sigmoid 和 tanh 更快。计算速度非常快，只需要判断输入是否大于0。

3）收敛速度远快于sigmoid和tanh

4）ReLU的非饱和性可以有效地解决梯度消失的问题，提供相对宽的激活边界。

5）ReLU的单侧抑制提供了网络的稀疏表达能力。

ReLU也有几个需要特别注意的问题：

1）ReLU 函数的输出为 0 或正数，不是zero-centered

2）Dead ReLU Problem，指的是某些神经元可能永远不会被激活，导致相应的参数永远不能被更新。这是由于函数导致负梯度在经过该ReLU单元时被置为0，且在之后也不被任何数据激活，即流经该神经元的梯度永远为0，不对任何数据产生响应。当输入为负时，ReLU 完全失效，在正向传播过程中，这不是问题。有些区域很敏感，有些则不敏感。但是在反向传播过程中，如果输入负数，则梯度将完全为零，sigmoid 函数和 tanh 函数也具有相同的问题。有两个主要原因可能导致这种情况产生：(1) 非常不幸的参数初始化，这种情况比较少见；(2) learning rate太高导致在训练过程中参数更新太大，会导致超过一定比例的神经元不可逆死亡，进而参数梯度无法更新，整个训练过程失败。解决方法是可以采用Xavier初始化方法，以及避免将learning rate设置太大或使用adagrad等自动调节learning rate的算法。

尽管存在这两个问题，ReLU目前仍是最常用的activation function，在搭建人工神经网络的时候推荐优先尝试！

3.4、Leaky ReLU

人们为了解决Dead ReLU Problem，提出了将ReLU的前半段设为0.01x而非0。

为什么 Leaky ReLU 比 ReLU 更好？

1）Leaky ReLU 通过把 x 的非常小的线性分量给予负输入（0.01x）来调整负值的零梯度（zero gradients）问题；

2）leak 有助于扩大 ReLU 函数的范围，通常 a 的值为 0.01 左右；

3）Leaky ReLU 的函数范围是（负无穷到正无穷）。

但另一方面， a值的选择增加了问题难度，需要较强的人工先验或多次重复训练以确定合适
的参数值。

注意：从理论上讲，Leaky ReLU 具有 ReLU 的所有优点，而且 Dead ReLU 不会有任何问题，但在实际操作中，尚未完全证明 Leaky ReLU 总是比 ReLU 更好。

3.5、ELU (Exponential Linear Units，指数的线性单元) 函数

ELU 的提出也解决了 ReLU 的问题。与 ReLU 相比，ELU 有负值，这会使激活的平均值接近零。均值激活接近于零可以使学习更快，因为它们使梯度更接近自然梯度。

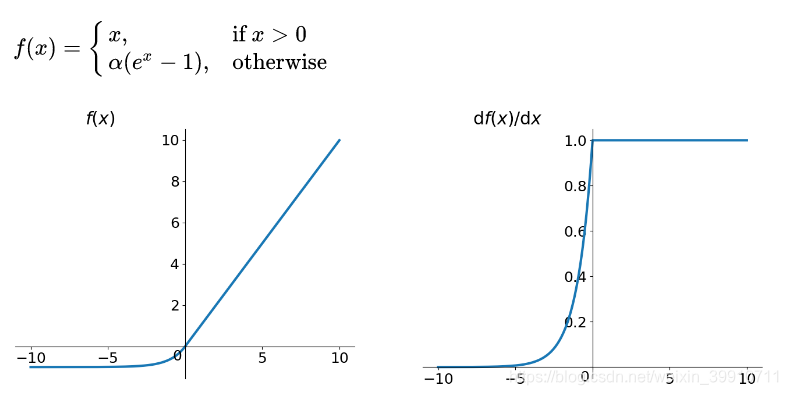
显然，ELU 具有 ReLU 的所有优点，并且：

1）没有 Dead ReLU 问题，输出的平均值接近 0，以 0 为中心；

2）ELU 通过减少偏置偏移的影响，使正常梯度更接近于单位自然梯度，从而使均值向零加速学习；

3）ELU 在较小的输入下会饱和至负值，从而减少前向传播的变异和信息。

一个小问题是它的计算强度更高。与 Leaky ReLU 类似，尽管理论上比 ReLU 要好，但目前在实践中没有充分的证据表明 ELU 总是比 ReLU 好。

3.6、PReLU（Parametric ReLU）

PReLU 也是 ReLU 的改进版本,想法是基于参数的方法，即Parametric ReLU：，其中可由back propagation学出来。

Kaiming He的论文《Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification》指出，不仅可以训练，而且效果更好。

看一下 PReLU 的公式：参数α通常为 0 到 1 之间的数字，并且通常相对较小。

如果 a_i= 0，则 f 变为 ReLU
如果 a_i> 0，则 f 变为 leaky ReLU
如果 a_i 是可学习的参数，则 f 变为 PReLU

PReLU 的优点如下：

在负值域，PReLU 的斜率较小，这也可以避免 Dead ReLU 问题。
与 ELU 相比，PReLU 在负值域是线性运算。尽管斜率很小，但不会趋于 0。

3.7、Softmax

Softmax 是用于多类分类问题的激活函数，在多类分类问题中，超过两个类标签则需要类成员关系。对于长度为 K 的任意实向量，Softmax 可以将其压缩为长度为 K，值在（0，1）范围内，并且向量中元素的总和为 1 的实向量。

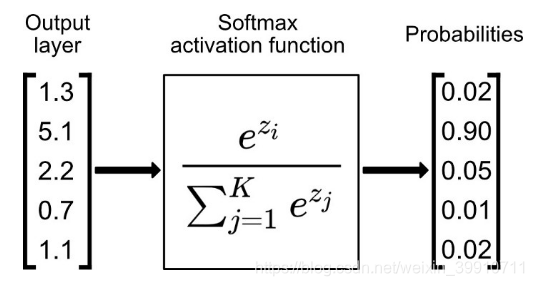
Softmax 与正常的 max 函数不同：max 函数仅输出最大值，但 Softmax 确保较小的值具有较小的概率，并且不会直接丢弃。我们可以认为它是 argmax 函数的概率版本或「soft」版本。

Softmax 函数的分母结合了原始输出值的所有因子，这意味着 Softmax 函数获得的各种概率彼此相关。

Softmax 激活函数的主要缺点是：

在零点不可微；
负输入的梯度为零，这意味着对于该区域的激活，权重不会在反向传播期间更新，因此会产生永不激活的死亡神经元。

3.8、Swish

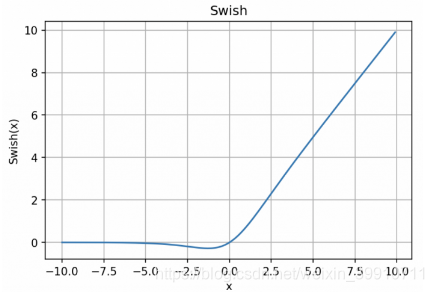
函数表达式：y = x * sigmoid (x)

Swish 的设计受到了 LSTM 和高速网络中 gating 的 sigmoid 函数使用的启发。我们使用相同的 gating 值来简化 gating 机制，这称为 self-gating。

self-gating 的优点在于它只需要简单的标量输入，而普通的 gating 则需要多个标量输入。这使得诸如 Swish 之类的 self-gated 激活函数能够轻松替换以单个标量为输入的激活函数（例如 ReLU），而无需更改隐藏容量或参数数量。

Swish 激活函数的主要优点如下：

「无界性」有助于防止慢速训练期间，梯度逐渐接近 0 并导致饱和；（同时，有界性也是有优势的，因为有界激活函数可以具有很强的正则化，并且较大的负输入问题也能解决）；
导数恒 > 0；
平滑度在优化和泛化中起了重要作用。

3.9 Maxout

这个函数可以参考论文《maxout networks》，Maxout是深度学习网络中的一层网络，就像池化层、卷积层一样等，我们可以把maxout 看成是网络的激活函数层，我们假设网络某一层的输入特征向量为：X=（x1,x2,……xd），也就是我们输入是d个神经元。Maxout隐藏层每个神经元的计算公式如下：

上面的公式就是maxout隐藏层神经元i的计算公式。其中，k就是maxout层所需要的参数了，由我们人为设定大小。就像dropout一样，也有自己的参数p(每个神经元dropout概率)，maxout的参数是k。公式中Z的计算公式为：

权重w是一个大小为(d,m,k)三维矩阵，b是一个大小为(m,k)的二维矩阵，这两个就是我们需要学习的参数。如果我们设定参数k=1，那么这个时候，网络就类似于以前我们所学普通的MLP网络。
我们可以这么理解，本来传统的MLP算法在第i层到第i+1层，参数只有一组，然而现在我们不这么干了，我们在这一层同时训练n组的w、b参数，然后选择激活值Z最大的作为下一层神经元的激活值，这个max（z）函数即充当了激活函数。

在 Maxout 层，激活函数是输入的最大值，因此只有 2 个 maxout 节点的多层感知机就可以拟合任意的凸函数。

单个 Maxout 节点可以解释为对一个实值函数进行分段线性近似 (PWL) ，其中函数图上任意两点之间的线段位于图（凸函数）的上方。

Maxout 也可以对 d 维向量（V）实现：

假设两个凸函数 h_1(x) 和 h_2(x)，由两个 Maxout 节点近似化，函数 g(x) 是连续的 PWL 函数。

因此，由两个 Maxout 节点组成的 Maxout 层可以很好地近似任何连续函数。

3.10 Softplus

Softplus 函数：f（x）= ln（1 + exp x）

Softplus 的导数为

f ′(x)=exp(x) / ( 1+exp⁡ x )

= 1/ (1 +exp(−x ))

，也称为 logistic / sigmoid 函数。

Softplus 函数类似于 ReLU 函数，但是相对较平滑，像 ReLU 一样是单侧抑制。它的接受范围很广：(0, + inf)。

4 应用中如何选择合适的激活函数？

这个问题目前没有确定的方法，凭一些经验吧。

1）深度学习往往需要大量时间来处理大量数据，模型的收敛速度是尤为重要的。所以，总体上来讲，训练深度学习网络尽量使用zero-centered数据 (可以经过数据预处理实现) 和zero-centered输出。所以要尽量选择输出具有zero-centered特点的激活函数以加快模型的收敛速度。

2）如果使用 ReLU，那么一定要小心设置 learning rate，而且要注意不要让网络出现很多 “dead” 神经元，如果这个问题不好解决，那么可以试试 Leaky ReLU、PReLU 或者 Maxout.

3）最好不要用 sigmoid，你可以试试 tanh，不过可以预期它的效果会比不上 ReLU 和 Maxout.

转自：激活函数（Activation Function）-CSDN博客