基于频域的数字图像水印算法设计

打工人枭臣

已于 2022-08-31 15:32:27 修改

阅读量2.3k

点赞数 3

分类专栏：数字图像处理文章标签：算法图像处理傅里叶分析

于 2022-08-31 15:03:47 首次发布

本文链接：https://blog.csdn.net/fx0925/article/details/126622845

版权

数字图像处理专栏收录该内容

1 篇文章

订阅专栏

1、设计方案的整体框架及可行性分析

1.1设计思路

整体框架图

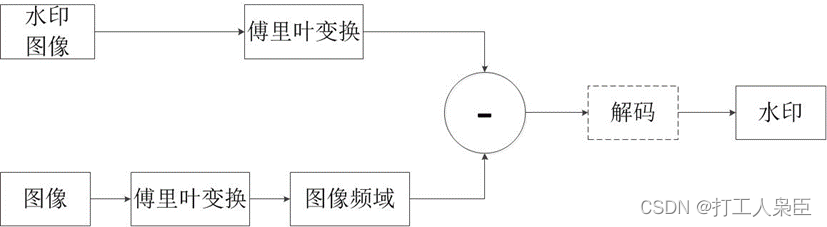
1.2方案可行性分析

（1）数字水印基本原理

1.傅里叶变换

图像本身在计算机中核心的存储是矩阵, 可以看做二维信号, FFT 的应用使得傅里叶变换得以实现. 设二维离散信号 $f(x,y)$ 表示大小为 $M*N$ 的一幅数字图像, 则二维离散傅立叶变换定义如下

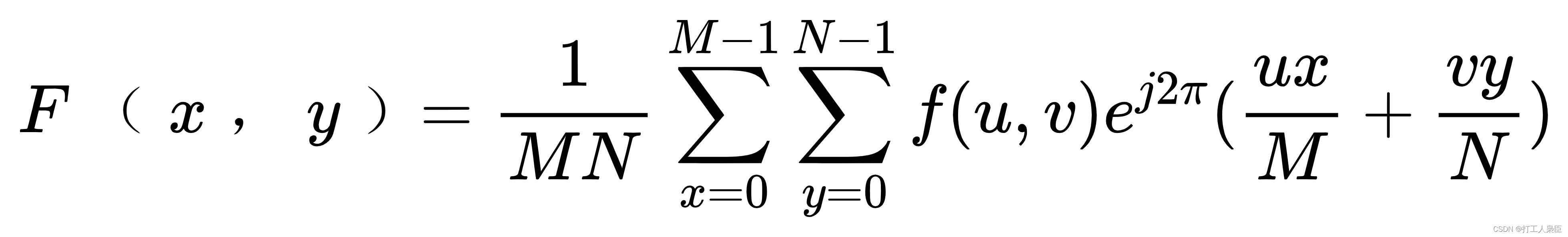
也可以用向量形式表示:

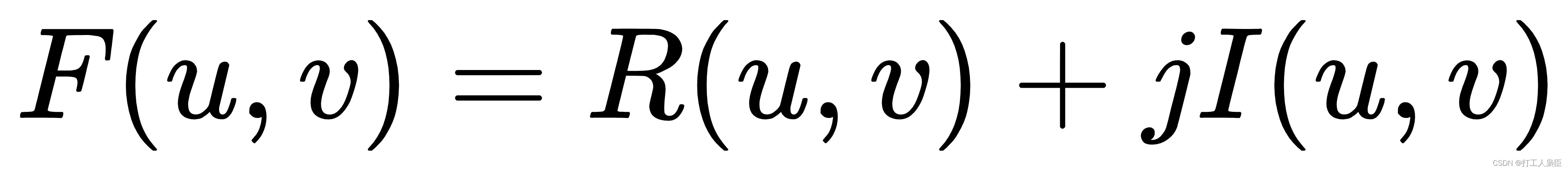
频谱:

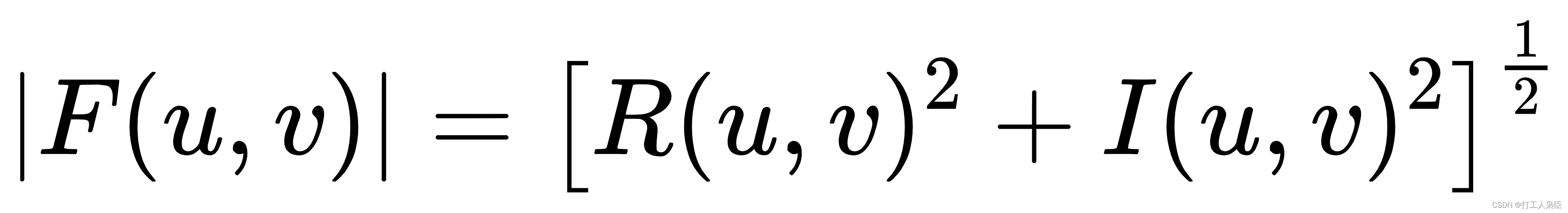
相位谱:

功率谱(能量谱):

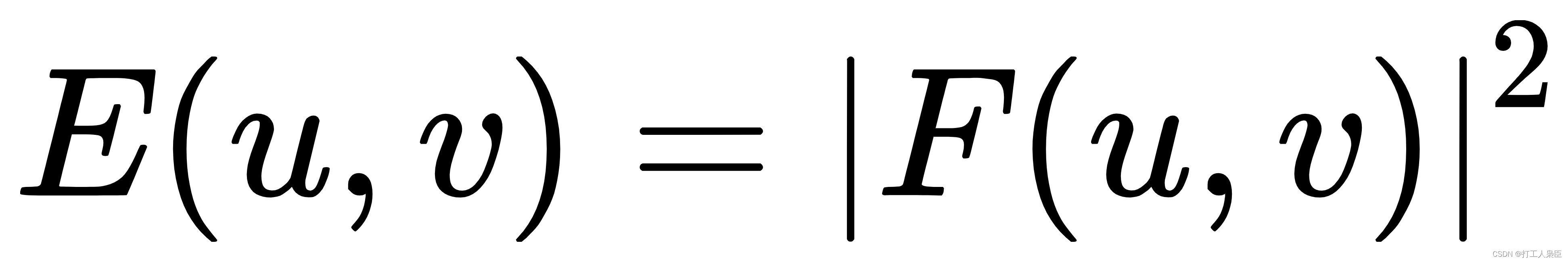
（3）Arnold置乱和逆置乱的数学公式

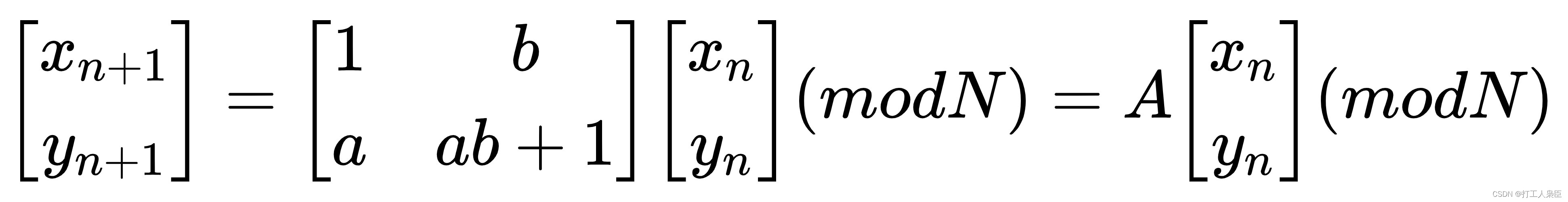
$x_{n},y_{n}$ 表示像素在原图像中的坐标， $x_{n+1},y_{n+1}$ 表示变换后的像素坐标，a,b为参数，均为正整数且都小于N，变换矩阵行列式满足∣A∣=1，则可逆。因此如下为逆置乱公式：

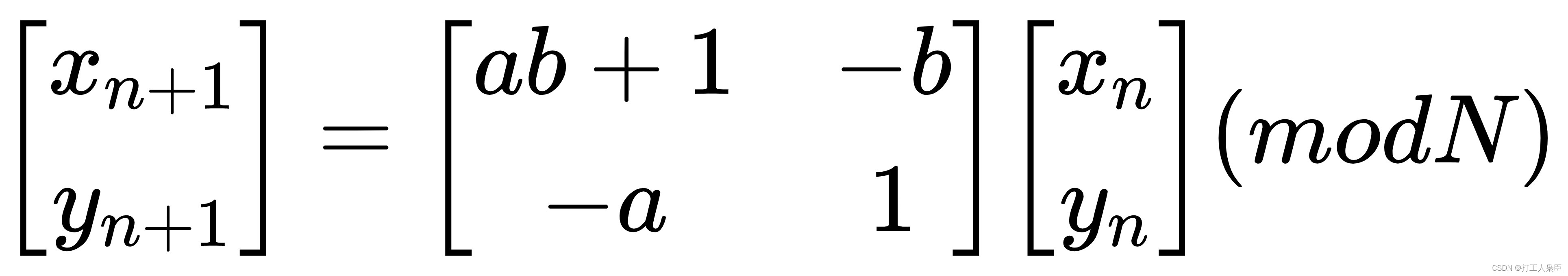
由此可以看到，只要知道参数ab且知道变换次数的情况下，才能让置乱后的图像复原。

2、设计方案的实现及实验结果分析

2.1 水印的嵌入

在水印嵌入时，需要载入宿主图像和水印图像，在获得含水印图像后，需要保存含水印的图像,对于这些打开与保存的操作，MATLAB中均提供了相应的函数，用户开发时进行调用即可实现文件操作功能.宿主图像载入的方法如下:

function [I]=qianru(I,G)

alpha=0.2

for p=1:64

for q=1:64

BLOCK1=I(((p-1)*8+1):p*8,((q-1)*8+1):q*8);

BLOCK1=dct2(BLOCK1);

BLOCK1(4,5)=BLOCK1(4,5)+ alpha*G(p,q);

BLOCK1=idct2(BLOCK1);

I(((p-1)*8+1):p*8,((q-1)*8+1):q*8)= BLOCK1;

end

结果分析：通过二维离散傅里叶变换将水印嵌入到原始图像中去，通过alpha可更改嵌入水印的程度

2.2 水印置乱

for n=1:5

for u=1:64

for v=1:64

temp=tempImg(u,v);

ax=mod((u-1)+(v-1),64)+1;

ay=mod((u-1)+2*(v-1),64)+1;

outImg(ax,ay)=temp;

end

tempImg=outImg;

end

结果分析：用Arnold置乱，水印随机分布，得到置乱后的水印图像

2.3水印的提取

在水印的提取模块，用户首先载入含水印的图像,然后载入原始宿主图像即可提取出嵌入在图像中的水印。通过载入原始水印图像，即可对提取出的水印与原始水印进行相关性比较，以评价算法的实现效果。

function [Y] = tiqu(I,W)

for p=1:64

for q=1:64

BLOCK1=W(((p-1)*8+1):p*8,((q-1)*8+1):q*8);

BLOCK2=I(((p-1)*8+1):p*8,((q-1)*8+1):q*8);

BLOCK1=dct2(BLOCK1);

BLOCK2=dct2(BLOCK2);

Y(p,q)=(BLOCK1(4,5)-BLOCK2(4,5))/0.2;

end

for n=1:43 %循环次数48-5

for u=1:64

for v=1:64

temp1=Y(u,v);

bx=mod((u-1)+(v-1),64)+1;

by=mod((u-1)+2*(v-1),64)+1;

outImg1(bx,by)=temp1;

end

Y=outImg1;

end

结果分析：经过反置乱操作，成功将水印提取。

2.4攻击测试

（1）压缩攻击：imwrite(W,'attack.jpg','jpeg','Quality',15); %压缩比默认75

结果分析：压缩比默认75，改变图片格式，提取出的水印效果较差，无法识别原水印图像。

（2）剪切攻击：

Q_r= B(:,:,1);

Q_r(1:128,1:32)=255;

Q_g =B(:,:,2);

Q_g(1:128,1:32)=255;

Q_b =B(:,:,3);

Q_b(1:128,1:32)=255;

B(:,:,1) = Q_r;

B(:,:,2) = Q_g;

B(:,:,3) = Q_b;

figure(3);

subplot(3,2,6);imshow(B,[]);title('剪切攻击图像');

结果分析：经实验发现，剪切比例越小，提取的水印效果较差。

（3）噪声攻击：

W1=imnoise(W,'gaussian',0,0.001);figure;imshow(attack),title('噪声攻击');

W2=imnoise(W,'salt',0.02);

结果分析：加入噪声是对水印鲁棒性考验的一种常见的攻击。本实验分别是在嵌入水印的图像中强度为0.02的高斯噪声、强度为0.02的椒盐噪声并从中提取水印，结果显示抗椒盐噪声性能优于高斯噪声。

2.5 性能评价

对水印算法的性能评价有：

归一化相关系数（Normalized Coefficient，NC）
峰值信噪比（Peak Signal to Noise Ratio，PSNR）

表2.5.1性能评价

攻击类型	归一化相关系数	峰值信噪比
高斯噪声	0.7878	3.6637
椒盐噪声	0.9103	7.8413
旋转逆时针1°	-0.0077	0.1813
压缩攻击	-0.0211	0.7025
剪切攻击	0.9912	18.3473

3、设计结论

本文在算法设计上为了确保数字图像信息的传输安全性和保密性，在水印嵌入前，对载体图像信息采用了图像置乱技术，实现信息的加密效果，同时在对图像进行还原的时候通过反变换实现图像信息的解密。其中应对噪声攻击和剪切攻击取得了较好的效果，剪切攻击后提取的水印不太理想。

参考文献

[1]赵颖.基于数字水印技术的图像信息安全应用研究[J].信息化研究,2021,47(01):15-19.

[2]毛新光.基于二维码图像的数字水印算法的研究[J].网络安全技术与应用,2022,(02):29-31.

[3]张明贵,高静.一种抗数字印刷/拍摄的数字水印算法研究及验证[J].包装工程,2022,43(03):274-283.

[4]万谊丹.基于Arnold和DCT的抗剪切攻击图像水印研究[J].网络安全技术与应用,2021,(08):40-41.

[5]傅楚君,兰胜坤.基于DCT变换的数字水印算法[J].网络安全技术与应用,2020,(07):49-51.

特别说明：

如需资源可到如下文章下载，本人原创，内有运行说明、程序附录，Matlab打开即可运行，结果与本文一致。基于频域的数字图像水印算法设计，水印嵌入，数字图像产权保护-Matlab文档类资源-CSDN下载互联网和多媒体技术的发展，使更多的数字作品得以借助网络发表，在方便了交流的同时作品的原创性和安全性也更多下载资源、学习资料请访问CSDN下载频道.https://download.csdn.net/download/fx0925/86504479