hiho 4 Trie 图

问题描述：

给定N个字符串组成的一个词典 和 一个长为L的字符串S ， 求S中是否存在词典中的字符串。

解决方法：

之前文章写过Trie树的方法记录一个词典，如果使用Trie树记录了词典中的所有词条，最长的词条为M，从前到后枚举S的每个位置，以当前位置为起点，使用Trie树进行比较，就可以判断是否存在。复杂度是O(M*L)。
是否存在时间复杂度更低的方法？首先，我们找上面方法的冗余比较：
比如下面的例子：

序号	1	2	3	4
str	a	b	c	d
dic	a	b	c	？

在第四个位置处不匹配，此时移时要移动dic 到序号2，并从头开始比较：

序号	1	2	3	4
str	a	b	c	d
dic		？

不匹配，再次移动：

序号	1	2	3	4
str	a	b	c	d
dic			c	d

成功找到。
其实，第二个位置的匹配是冗余的，因为第一次匹配过程中知道str[1~3] = dic[1~3], 也就是知道了str[2] = dic[2] = b, 而dic[1] $\ne$b 所以在第一次比较中就已经可以预测到第二次比较是不成功的。
这部分类似KMP算法，每次不匹配的时候，不是从头开始比较，而是移动模式串。
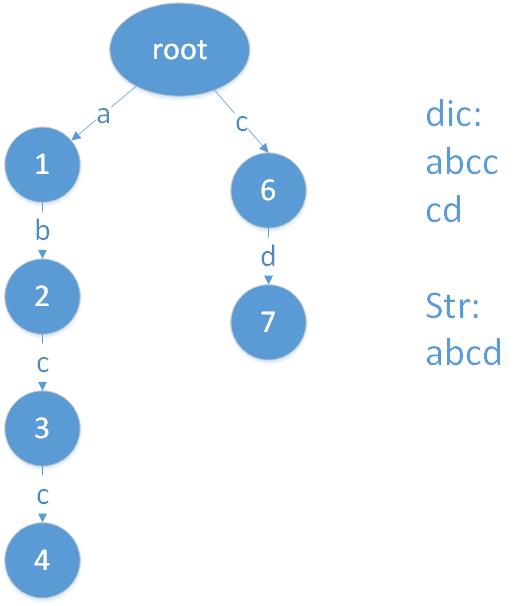
如下图：

注：没有全部添加。
在Trie树的基础上，添加一些边，使得在每个节点处对于每个字符都有一个对应的出边。
要添加这些边，如上图现在要添加节点4的出边，首先已经有了字符为’c’的出边，要添加a, b, d 三条出边。首先找到节点4对应字符串“ab”在Trie树中的最长后缀节点，观察可得为2，就可以添加4–a–>1, 4–b–>2, 4–d–>0 三条边。
我们只需要知道当前节点n对应的最长后缀节点trie(n)，如果trie(n)的对所有字符都有一个出边，我们就可以补充上当前节点n缺少的边。
trie(n)节点所在树的层数一定小于n所在树的层数，可以使用广度优先搜索，保证trie(n)的所有边已经添加。
现在问题是求最长后缀节点trie(n)，回忆在KMP算法中的next数组递归求解过程。这里我们首先找到n的父节点f， 且存在f –c–>n这条边，我们已知f的最长后缀节点trie(f)，然后再找到trie(f)–c–>P 这条边，这样就找到了trie(n) = P。
代码如下：

#include <cstdio>
#include <cstring>
#include <queue>
enum{maxm= 1000000+5, maxn = 1000+5};
struct Node{
    int next[26];
    int trie;
    bool leaf;
};
Node tree[maxm];
int tNum = 0;
char s[maxm];
void add()
{
    int rt, i;
    for(rt =0, i=0; s[i]; rt = tree[rt].next[s[i]-'a'], i++)
    {
        if (!tree[rt].next[s[i]-'a'])
            tree[rt].next[s[i]-'a'] = tNum++;
    }
    tree[rt].leaf = true;
}
std::queue<int> q;
void buildTree()
{
    tree[0].trie = 0;
    for (int i=0; i< 26; i++)
    {
        int rt = tree[0].next[i];
        if (rt)
        {
            tree[rt].trie = 0;
            q.push(rt);
        }
    }

    while(!q.empty())
    {
        int rt = q.front();
        q.pop();

    // !!! 不要漏掉，
        if (tree[tree[rt].trie].leaf)
            tree[rt].leaf = true;

        for (int i=0; i< 26; i++)
        {
            int trie = tree[tree[rt].trie].next[i];// 与KMP 不同， next 是已知的不需要循环查找
            int ch = tree[rt].next[i];
            if (ch)
            {
                tree[ch].trie = trie;
                q.push(ch);
            }else{
                tree[rt].next[i] = trie;
            }
        }
    }
}
bool find()
{
    if (tree[0].leaf)
        return true;

    int j =0;
    for (int i=0; s[i]; i++)
    {
        j = tree[j].next[s[i]-'a'];
        if (tree[j].leaf)
            return true;
    }
    return false;
}
int main()
{
    //freopen("in.txt", "r", stdin);
    int w;
    scanf("%d", &w);
    memset(tree, 0, sizeof(tree));
    tNum = 1;
    while(w--)
    {
        scanf("%s", s);
        add();
    }
    buildTree();
    scanf("%s", s);
    printf("%s\n", find()? "YES":"NO");
    return 0;
}

1，第0层的trie = 0；