深度学习笔记8：卷积的矩阵实现

上一篇文章中对卷积进行概念的说明，并且用for循环进行了运算和实现，但是从运算时间上看，明显很慢。
这次利用矩阵运算对卷积进行运算：





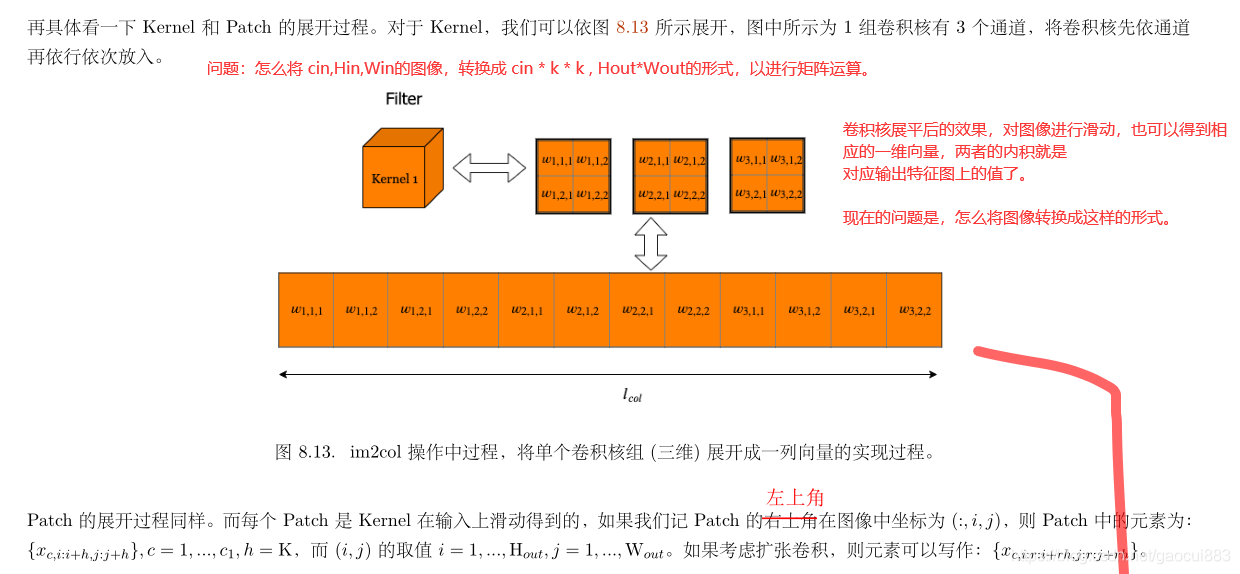
方法就应用矩阵索引的方法，从扩展后输入X 抓取需要计算的像素单元，也就是与上边黄色权重对应的相撞的图像块，只不过图像块此时与W都是一维展平的。

上图为行索引，下图为列索引，卷积核窗口在X图像上进行滑动的时候，行索引不变，列索引连续变化，滑动到尾部的时候，行索引加1，列索引从头开始继续变化，直到移动到右下角的单元格。

可以看到两个矩阵的行数都是 k k * n_in， 这就是与输入权重对应的窗口块。

列数都是 n_out, * n_out， 是输出窗口的大小。

两个矩阵对应位置的数字表示在 X中的坐标索引，从而可以抓取出来所有需要 进行卷积运算的窗口块，数量当然是 n_out * n_out。

矩阵索引操作：

a = np.asarray([[1,2,3],[4,5,6],[7,8,9]])
a
Out[29]: 
array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])
a.shape
Out[30]: (3, 3)
a[[1,2],[0,1]]
Out[31]: array([4, 8])
a[[1,2],:]
Out[32]: 
array([[4, 5, 6],
       [7, 8, 9]])
a[[[1,2],[1,2]],:]
Out[33]: 
array([[[4, 5, 6],
        [7, 8, 9]],
       [[4, 5, 6],
        [7, 8, 9]]])
a[[[1,2],[1,2]],[[0,1],[0,1]]]
Out[34]: 
array([[4, 8],
       [4, 8]])
a[[[1,2],[1,2]],[[0,1],[0,2]]]
Out[35]: 
array([[4, 8],
       [4, 9]])

只要每个维度的索引可以对应起来，或者可以进行广播，那么就可以取出相应位置的元素值。

因此，应用上边的两个行和列索引矩阵，就可以抓取X图像块的条状表示了。

卷积的矩阵实现：

# -*- coding: utf-8 -*- 

# time : 2021/5/6 15:02
# task: 
"""  用矩阵的乘法来进行卷积的运算"""

import numpy as np
from different_convolution import Pad2D
def _im2col_indices(x_shape, fr, fc, p, s, d=1):
    """ 计算各个索引"""
    pr1, pr2, pc1, pc2 = p
    n_ex, n_in, in_rows, in_cols = x_shape
    _fr, _fc = fr + (fr - 1) * (d - 1), fc + (fc - 1) * (d - 1)

    out_rows = int((in_rows + pr1 + pr2 - _fr + s) / s)
    out_cols = int((in_cols + pc1 + pc2 - _fc + s) / s)
    print(out_rows,out_cols)
    # 28 28
    i0 = np.repeat(np.arange(fr), fc)  # 000111222   * n_in.
    # 000111222
    i0 = np.tile(i0, n_in) * d

    i1 = s * np.repeat(np.arange(out_rows), out_cols)  # 00000..0 11111..1 2222..2.
    # 这里i1 的个数其实就是输出的图像的尺度的长宽大小。
    # 对于每一个位置，都需要相应的卷积得到结果。
    j0 = np.tile(np.arange(fc), fr * n_in)  # 相当与相对索引。
    j1 = s * np.tile(np.arange(out_cols), out_rows) # 相当于绝对索引。 i1 j1 确定位置， i0，j0 确定卷积。得到切块。
    i = i0.reshape(-1, 1) + i1.reshape(1, -1)
    # 第二个的索引。
    j = j0.reshape(-1, 1) + j1.reshape(1, -1)
    # 第三个索引。
    k = np.repeat(np.arange(n_in), fr * fc).reshape(-1, 1)
    return k, i, j


# k,i,j = _im2col_indices((10, 3, 28,28), 3,3, (1,1,1,1), s=1, d=1)
# print(k.shape)  # 27 1
# print(i.shape)  # 27 784
# [[ 0  0  0 ... 27 27 27]   # 自上而下的对应。 一共啊27 行，也就是27个卷积块。27 : k*k*n_in, 784: out*out
# #  [ 0  0  0 ... 27 27 27]
# #  [ 0  0  0 ... 27 27 27]
# #  ...
# #  [ 2  2  2 ... 29 29 29]
# #  [ 2  2  2 ... 29 29 29]
# #  [ 2  2  2 ... 29 29 29]]
# print(j.shape)  # 27 784

# [[ 0  1  2 ... 25 26 27]
#  [ 1  2  3 ... 26 27 28]
#  [ 2  3  4 ... 27 28 29]
#  ...
#  [ 0  1  2 ... 25 26 27]
#  [ 1  2  3 ... 26 27 28]
#  [ 2  3  4 ... 27 28 29]]
def im2col(X, W_shape, pad, stride, dilation=1):
    fr, fc, n_in, n_out = W_shape
    s, p, d = stride, pad, dilation
    n_samp, in_rows, in_cols, n_in = X.shape
    X_pad, p = Pad2D(X, p, W_shape[:2], stride=s, dilation=d)
    pr1, pr2, pc1, pc2 = p
    # 将输入的通道维数移至第二位
    X_pad = X_pad.transpose(0, 3, 1, 2)
    k, i, j = _im2col_indices((n_samp, n_in, in_rows, in_cols), fr, fc, p, s, d)
    # X_col.shape = (n_samples, kernel_rows*kernel_cols*n_in, out_rows*out_cols)
    X_col = X_pad[:, k, i, j]  # i,j,k 联合位置的元素值。形状与i，j，k 形状有关。
    X_col = X_col.transpose(1, 2, 0).reshape(fr * fc * n_in, -1)
    return X_col, p

def conv2D_gemm(X,W, stride=0, pad="same", dilation=1):
    s, d = stride, dilation
    _, p = Pad2D(X, pad, W.shape[:2], s, dilation=dilation)
    pr1, pr2, pc1, pc2 = p
    fr, fc, in_ch, out_ch = W.shape
    n_samp, in_rows, in_cols, in_ch = X.shape
    # 考虑扩张率
    _fr, _fc = fr + (fr - 1) * (d - 1), fc + (fc - 1) * (d - 1)
    # 输出维数，根据上面公式可得
    out_rows = int((in_rows + pr1 + pr2 - _fr) / s + 1)
    out_cols = int((in_cols + pc1 + pc2 - _fc) / s + 1)
    # 将 X 和 W 转化为 2D 矩阵并乘积
    X_col, _ = im2col(X, W.shape, p, s, d)
    W_col = W.transpose(3, 2, 0, 1).reshape(out_ch, -1)
    Z = (W_col @ X_col).reshape(out_ch, out_rows, out_cols, n_samp).transpose(3, 1, 2, 0)
    return Z

运行时间比较：

(16, 17, 16, 17)
compute timing used 4.735801696777344  # 普通循环运算实现卷积。
(10, 32, 32, 64)
32 32
using time  : 0.005004167556762695 #矩阵运算实现卷积
(10, 32, 32, 64)