Partial Distance Correlation

特征函数

随机变量 X 的特征函数定义为：

$${\varphi }_X(t)\triangleq E[e^{itX}]={\int }_{-\infty }^{+\infty }{e}^{itx}f(x)dx$$

其中 $f_X(x)$ 为连续随机变量的概率密度函数。

特征函数的一些性质如下：

• $Y=X_1+X_2$，$X_1,X_2$相互独立，则 ${\varphi }_Y(t)={\varphi }_{X_1}(t)\cdot {\varphi }_{X_2}(t)$
• $Y=aX+b$， 则 ${\varphi }_Y(t)=e^{itb}\cdot {\varphi }_X(at)$
• $X\sim \mathcal{N}(0,1)$ 则 ${\varphi }_X(t)=e^{-t^2/2}$

联合特征函数

连续随机变量$X,Y$的联合合同函数定义为

$${\varphi }_{X,Y}(v,w)\triangleq E[e^{i(vx+wy)}]={\int }_{-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }{e}^{i(vx+wy)}{f}_{XY}(x,y)dxdy$$

性质：

• ${\varphi }_{X,Y}(0,0)=1$
• ${\varphi }_{X,Y}(v,0)={\varphi }_X(v),{\varphi }_{X,Y}(0,w)={\varphi }_Y(w)$
• $|{\varphi }_{X,Y}(v,w)|\le 1$
• 当 X 与 Y 独立，则 ${\varphi }_{X,Y}(v,w)={\varphi }_X(v){\varphi }_Y(w)$

$||\cdot |{|}_w$范数

对于$R^p\times R^q$ 上的复函数 $\gamma (t,s)$，$||\cdot |{|}_w$范数的定义为：

$$||\gamma (t,s)|{|}_w^2={\int }_{R^{p+q}}|\gamma (t,s){|}^2\omega (t,s)dtds$$

其中权重函数$\omega (t,s)$为正且积分存在，$|\gamma (t,s){|}^2=\gamma (t,s)\overline{\gamma (t,s)}$

Distance Correlation

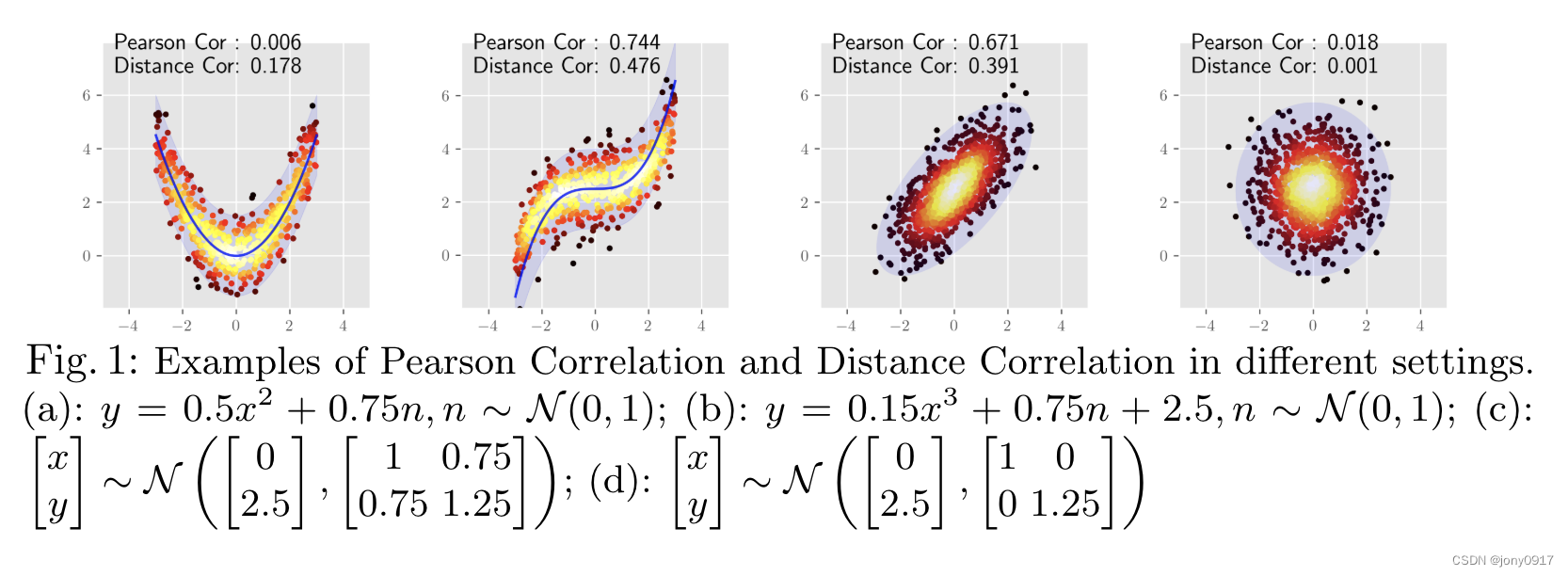
任意维度随机变量$X\in R^p,Y\in R^q$ 的 Distance Covariance 定义为:

$${\mathcal{V}}^2(X,Y):=||{\varphi }_{X,Y}(t,s)-\varphi (t{)}_X{\varphi }_Y(s)|{|}^2={\int }_{R^{p+q}}|{\varphi }_{X,Y}(t,s)-{\varphi }_X(t){\varphi }_Y(s){|}^{2}w(t,s)dtds,w(t,s)=(|t{|}_p^{1+p}|s{|}_q^{1+q}{)}^{-1}$$

随机变量 $X\in R^p$ Distance Variance 的定义为:

$${\mathcal{V}}^2(X,X)=||{\varphi }_{X,X}(t,s)-{\varphi }_X(t){\varphi }_X(s)|{|}^2$$

随机变量$X\in R^p,Y\in R^q$ 的 Distance Correlation 定义为:

$${\mathcal{R}}^2(X,Y)=\{\begin{array}{rcl}\frac{{\mathcal{V}}^2(X,Y)}{\sqrt{{\mathcal{V}}^2(X){\mathcal{V}}^2(Y)}}& & \sqrt{{\mathcal{V}}^2(X){\mathcal{V}}^2(Y)}>0\\ 0& & \sqrt{{\mathcal{V}}^2(X){\mathcal{V}}^2(Y)}=0\end{array}$$

$\mathcal{V}$ 用于衡量联合特征函数与边缘特征函数乘积的距离$||{\varphi }_{X,Y}(t,s)-{\varphi }_X(t){\varphi }_Y(s)||$，并应用于独立性假设检验：

$$H_0:{\varphi }_{X,Y}(t,s)={\varphi }_X(t){\varphi }_Y(s)vs{H}_1:{\varphi }_{X,Y}(t,s)\ne {\varphi }_X(t){\varphi }_Y(s)$$

经验 Distance Covariance & Distance Corelation ：

$$(x_i,y_i)\sim (X,Y)$$

$$a_{ij}=||x_i-x_j||,{\overline{a}}_{.j}=\frac{1}{n}\sum _{i=1}^n{a}_{ij},{\overline{a}}_{i.}=\frac{1}{n}\sum _{j=1}^n{a}_{ij},{\overline{a}}_{..}=\frac{1}{n^2}\sum _{i=1}^n\sum _{j=1}^n{a}_{ij}$$

$$A_{ij}=a_{ij}-{\overline{a}}_{.j}-{\overline{a}}_{i.}+{\overline{a}}_{..}$$

$${\mathcal{V}}_n^2(X,Y)=\frac{1}{n^2}\sum _{i=1}^n\sum _{j=1}^n{A}_{ij}{B}_{ij}$$

$${\mathcal{V}}_n^2(X)=\frac{1}{n^2}\sum _{i=1}^n\sum _{j=1}^n{A}_{ij}^2$$

$${\mathcal{R}}_n^2(X,Y)=\{\begin{array}{rcl}\frac{{\mathcal{V}}_n^2(X,Y)}{\sqrt{{\mathcal{V}}_n^2(X){\mathcal{V}}_n^2(Y)}}& & \sqrt{{\mathcal{V}}_n^2(X){\mathcal{V}}_n^2(Y)}>0\\ 0& & \sqrt{{\mathcal{V}}_n^2(X){\mathcal{V}}_n^2(Y)}=0\end{array}$$

距离相关系数的一些性质：

• 当 $E|X{|}_p<\infty ,E|Y|q<\infty$，则 $li{m}_{n\to \infty }{\mathcal{V}}_n(X,Y)=V(X,Y)$

• 当 $E(|X{|}_p+|Y{|}_q)<\infty$, 则 ${\lim }_{n\to \infty }{\mathcal{R}}_n^2(X,Y)=(R)(X,Y)$

• 当 $E(|X{|}_p+|Y{|}_q)<\infty$，则 $0\le \mathcal{R}\le 1$，当且仅当X与Y独立$\mathcal{R}=0$

• $0\le {\mathcal{R}}_n\le 1$

• 如果 $\mathcal{R}(X,Y)=1$, 则 $\exists a,b,C$, 满足$Y=a+bXC$

• $\mathcal{V}(X)=0$，则 $X=E[X]$

• $\mathcal{V}(a+bCX)=|b|\mathcal{V}(X)$

• $\mathcal{V}(X+y)\le \mathcal{V}(X)+\mathcal{V}(Y)$

总体 ${\mathcal{V}}^2(X,Y)$ 的无偏估计：

设 $A=(a_{ij})\in R^{n\times n}$ 为对称实数方阵，对角线元素为零，方阵A的 $\mathcal{U}$ 中心化矩阵 $\tilde{A}$ 定义为：

$${\tilde{A}}_{i,j}=\{\begin{array}{rcl}{a}_{ij}-\frac{1}{n-2}{\sum }_{i=1}^n{a}_{ij}-\frac{1}{n-2}{\sum }_{j=1}^n{a}_{ij}+\frac{1}{(n-1)(n-2)}{\sum }_{i=1}^n{\sum }_{j=1}^n{a}_{ij}& & i\ne j\\ 0& & i=j\end{array}$$

设$A=(a_{ij})$为随机变量 X 的一批样本 $x_1,..,x_n$ 的欧式距离矩阵， $B=(b_{ij})$ 为随机变量 Y 的样本 $y_1,....,y_n$ 的欧式距离矩阵，当 $E[X+Y]<\infty$ 且 $n>3$， 则 $(\tilde{A}\cdot \tilde{B})=\frac{1}{n(n-3)}{\sum }_{i=1}^n{\sum }_{j=1}^n{\tilde{A}}_{ij}{\tilde{B}}_{ij}$ 为总体 ${\mathcal{V}}^2(X,Y)$的无偏估计量。

Hilbert Space

H n = { A ~ : A ∈ S n } \mathcal{H}_n=\{\tilde{A}:A\in \mathcal{S}_n\} Hn​={A~:A∈Sn​} 为一个Hilbert space ，其中任意 $A=(A_{i,j}),B=(B_{i,j})$ 内积运算定义为：

$$(A\cdot B)=\frac{1}{n(n-3)}\sum _{i\ne j}{A}_{ij}{B}_{ij}$$

Partial Distance Covariance & Partial Distance Correlation

随机变量 $X,Y,Z$ 的样本距离矩阵分别记为$A,B,C$，样本Partial Distance Covariance 的定义为：

$$pdCov(X,Y;Z)\triangleq ({\tilde{A}}_{\perp \tilde{C}}\cdot {\tilde{B}}_{\perp \tilde{C}})$$

其中 ${\tilde{A}}_{\perp \tilde{C}}=\tilde{A}-\frac{(\tilde{A}\cdot \tilde{C})}{(\tilde{C}\cdot \tilde{C})}\tilde{C},{\tilde{B}}_{\perp \tilde{C}}=\tilde{B}-\frac{(\tilde{B}\cdot \tilde{C})}{(\tilde{C}\cdot \tilde{C})}\tilde{C}$

样本 Partial Distance Correlation 的定义为：

$$pdCor(X,Y;Z)=\frac{({\tilde{A}}_{\perp \tilde{C}}\cdot {\tilde{B}}_{\perp \tilde{C}})}{|{\tilde{A}}_{\perp \tilde{C}}||{\tilde{B}}_{\perp \tilde{C}}|}$$