系列文章目录
Python 机器学习入门之单变量线性回归
目录
前言
随着人工智能的不断发展,ai相关专业受到了许多人的青睐,机器学习这门技术作为ai的基础,很多人都走上了了学习机器学习的道路,但是课堂上老师讲的和用的教材.....
作者我是深受其害
一堆问号,感觉跳过了好多事情
神经网络是什么?
一层层的神经网络为什么能解决问题?
…
本文就介绍了机器学习的基础内容,为了那些跟我那时候有同样烦恼的同学们。一步步用神经网络解决单变量线性回归的问题
因为是一开始入门学习嘛,例子当然是越简单越能够让人理解啦
所以这里我们先不使用真实世界的文件做处理,而是用numpy构建数据样本用来训练
我们要做的事是依照某一条回归直线准备数据,就像我们给电脑出道考题。
先准备好答案,再为其添加噪声使其杂乱,干扰他的思考过程,然后再通过神经网络训练出这一条回归直线,让他感受我们做数学题的痛苦 ,‘验证’神经网络是否有这个能力找出这条直线,也就是找到答案,完成在一堆数据中线性回归的任务。
提示:本文中给的代码示例都是采用注释写在该行代码上方的方式
一、准备数据
下面是实现构建数据样本的函数,既然是用numpy构建,不要忘记import numpy哦?
建议为项目单独建立一个新的文件夹
将这个函数写在单独py文件下,这是为了文件结构可复用,后面会详细讲到
import numpy as np
from pathlib import Path
#文件名可以自定义,后缀不能随便改
file_name='train_file.npz'
#创建样本文件的函数
def CreateSampleData(m):
#创建path对象的目的是调用pathlib里的exist函数判断文件是否存在
#用指定的文件名创建path对象
file = Path(file_name)
#如果文件存在的话
if file.exists():
#用numpy的load方法读取文件
data = np.load(file)
#用data表格的data列作为自变量
X = data["data"]
#用data表格的label列作为因变量
Y = data["label"]
else:
#如果文件不存在的话
#使用Numpy模块创建一个大小为(m, 1)的二维随机数组。
#其中,np是Numpy模块的别名,random是该模块的子模块,
#random((m,1))是该子模块的方法之一,可以生成一个(0,1)之间均匀分布的随机数数组。
#该数组的大小为(m,1)。其中,m是当你调用函数是传进来的参数,是样本数目,可以是任意正整数。
#这个数组有m行,每行只有1列
X = np.random.random((m,1))
#将构建因变量的函数写成另一个函数
#这种封装能够提升函数的可读性,代码功能多了也便于管理
Y = TargetFunction(X)
#保存numpy文件,文件名是自己之前设定的file_name
np.savez(file_name, data=X, label=Y)
return X, Y
def TargetFunction(X):
#构建因变量的函数
#这行代码的作用是生成一个与`X`相同形状的随机噪声数组,
#其中每个元素都是从均值为0,标准差为0.2的正态分布中随机抽样得到的。
noise = np.random.normal(0,0.2,X.shape)
#手动为神经网络准备答案回归直线
#这里设置斜率为2、偏置为3
W = 2
B = 3
#根据直线方程y=wx+b为其准备因变量数组
Y = np.dot(X, W) + B + noise
return Y
生成结果示例
(实现函数在下面)
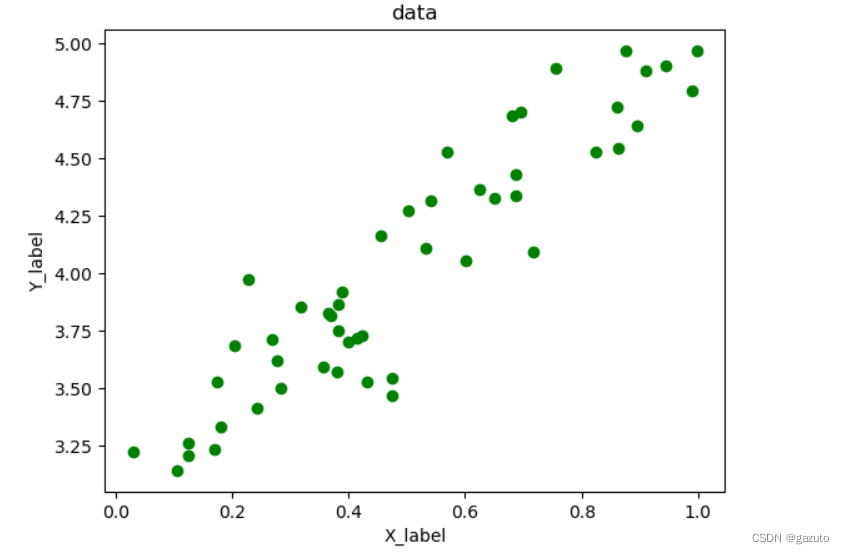
我做出来是这个样子,你们做出来也会是这样子(笑)
import matplotlib.pyplot as plt
def draw_data():
#加载数据文件
data = np.load(file_name)
#取出指定行,赋值到变量
X = data["data"]
Y = data["label"]
#遍历每一个xy值对,画出对应的散点图
for i in range(50):
plt.scatter(X[i], Y[i], marker='o', c='g')
plt.xlabel('X_label')
plt.ylabel('Y_label')
plt.title('data')
#展示出来
plt.show()
为什么是数组(矩阵)?
我们可以注意到,上面的运算都是采用让人看上去头大,很抽象难以想象出来,让人看着就想翻过去的矩阵。为什么要用这么麻烦的东西呢?
矩阵运算的确可能让人感到有些复杂和抽象,但是在很多数学、计算机科学和机器学习的应用场景中,矩阵运算是一种非常有效和高效的处理方式。因为尽管人类不擅长一次计算很多个数,但是计算机很擅长呀
举个例子,在深度学习中,神经网络可以使用矩阵运算快速地对图像、信号、文本等数据类型进行处理和转换。虽然矩阵运算在表达时可能看起来比较麻烦,但这种抽象的表示方法可以极大地简化模型计算的复杂度,从而加快模型训练的速度。就比如说同时计算多样本时,我们平时写的算式可能是
1 ∗ 1 1 * 1 1∗1+ 2 ∗ 2 2 * 2 2∗2+ 3 ∗ 3 3 * 3 3∗3
可是同样的计算用矩阵表达只需要
[
1
2
3
]
×
[
1
2
3
]
\begin{bmatrix} 1\\ 2\\ 3 \end{bmatrix} \times \begin{bmatrix} 1 &2&3 \end{bmatrix}
123
×[123]
此外,矩阵运算具有很好的数学性质,它们可以被方便地推导和证明。这对于优化算法、理论分析和数学建模都非常有用。所以,尽管矩阵运算可能看起来比较抽象和困难,但在现代计算机科学和机器学习领域中,这些运算是不可或缺的重要工具。
二、构建网络
0-1.神经网络的训练流程
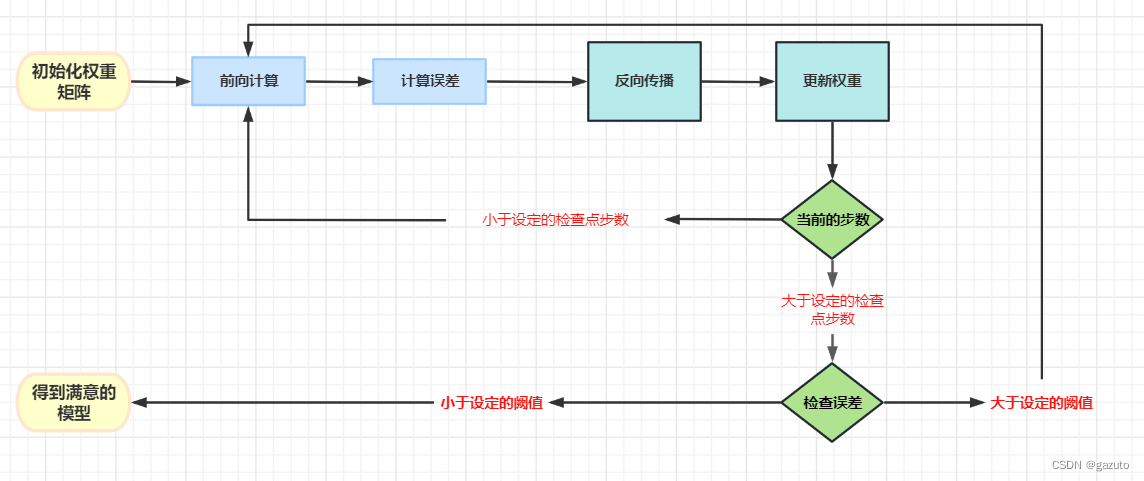
在构造程序让电脑一步步完成我们给出的‘题目’之前,我们首先要明白这个一根筋看起来不太聪明的黑铁块是怎么解决’题目‘的
在开始描述之前,请记住我下面提到的权重就是类似参数的集合的东西
比如说我们我们这里想训练出一条y=wx+b这样的直线
w和b就是我们这个任务里的权重
在训练神经网络的时候,首先先根据神经网络结构初始化权重矩阵
这里我们做线性回归,想训练一条直线一般来说只需要单点单层神经元
就像这样
[
w
1
w
2
w
3
]
\begin{bmatrix} w_1\\ w_2\\ w_3 \end{bmatrix}
w1w2w3
也可以零初始化,如果在线性回归这么做,那就是像是让我们的训练直线一开始趴在坐标轴上
就像这样
(这里下标是用于训练的输入数据样本数目,无需在意)
然后用输入的用来训练的数据进行前向计算得到预测值,
在我们这个项目中,就是
z
=
w
x
i
+
b
z=wx_i+b
z=wxi+b
(z代表预测值,为了与真实值区分开;x的下标代表样本数目)
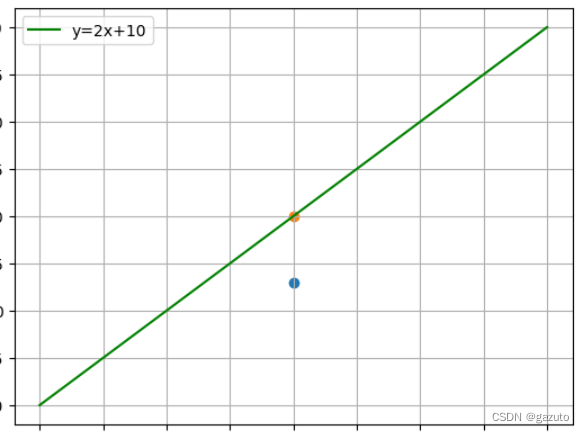
举个例子,假如我们训练出了一条y=2x+10的直线
前向计算得到预测值就是计算出黄点
如果蓝点是我们的一个输入数据,他就是我们的一个真实值
通过某种运算表达预测值与真实值之间的差距就叫做误差
这里的某种运算就是误差函数
计算误差,拿着预测值与真实值用设定好的误差函数的方式进行比对;
在做回归任务时,一般使用的误差函数是均方差函数:
M
S
E
=
1
n
∑
i
=
1
n
(
y
i
−
y
^
i
)
2
MSE = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2
MSE=n1i=1∑n(yi−y^i)2
我知道这个公式看起来很吓人,但是你们先别怕,我先跑
我们通过一个简单的例子来理解
假设我们同时使用两个样本进行训练,此时n=2,
z
1
=
2
,
z
2
=
4
,
y
1
=
3
,
y
2
=
6
M
S
E
=
1
2
[
(
2
−
3
)
2
+
(
4
−
6
)
2
]
{z}_1=2,{z}_2=4,{y}_1=3,y_2=6\\MSE= \frac{1}{2}[(2-3)^2+(4-6)^2]
z1=2,z2=4,y1=3,y2=6MSE=21[(2−3)2+(4−6)2]
(使用真实值而不是均值计算MSE函数,是因为在线性回归中,我们的目标是找到一个模型来预测给定的输入对应的输出。我们通过大量的训练数据来拟合这个模型,最终目标是让这个模型的预测结果尽可能地接近真实值。如果使用预测值的平均值计算MSE函数可能不够准确,因为平均值可能会受到一些异常值的影响。)
最后通过反向传播, 通过计算得出斜率与偏置需要如何变动才能得到真实值;
更新斜率与偏置,得到更接近答案直线的直线。
循环重复上述过程,以便训练出来的直线适用于所有数据
1.进行一次训练
前向计算
首先是前向计算:
我们希望得到一条形如y=wx+b的直线,
这里我们用x表示输入,y表示我们预设好的因变量,下标 i 表示其中一个样本,
用z表示预测值
所以前向计算就是
z
=
w
x
i
+
b
z=w{x}_i+b
z=wxi+b
(你看真的很简单吧hhh)
用代码表示是这样的:
(batch_x就是一打样本)
def __forwardBatch(self, batch_x):
Z = np.dot(batch_x, self.w) + self.b
return Z
反向传播
(数学部分)
前面我们已经说过,在线性回归中,一般使用的是均方差损失函数
M
S
E
=
1
n
∑
i
=
1
n
(
y
i
−
y
^
i
)
2
MSE = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2
MSE=n1i=1∑n(yi−y^i)2
这是我们最后想要训练出的函数:
z i = x i ⋅ w + b (1) z_i = x_i \cdot w + b \tag{1} zi=xi⋅w+b(1)
我们的目的是明白斜率(w)与偏置(b)需要如何变动才能得到真实值,并将其化到最简
但是真实值很难一次就“猜”出,特别是有很多数据样本的时候,我们首先要知道如何才能接近真实值,也就是尽力让误差函数的值降到最小。
在我们的这个项目里,就是需要让我们训练出的直线渐渐接近真实直线
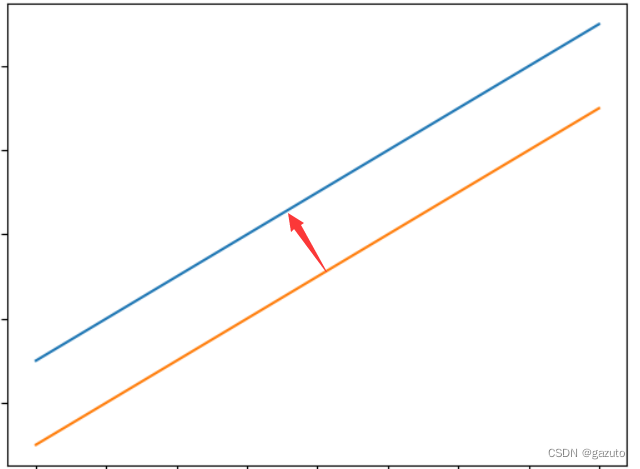
就像这样,要想逐步接近,我们需要知道要往哪个方向接近
我们先来看一个简单的例子
在这个例子里,这个点到两条直线的距离是一样的
假设我们要训练出一条经过这个点的直线,如果在此时用误差函数计算这两条直线的离真实值(这个点)的误差就会是一样的
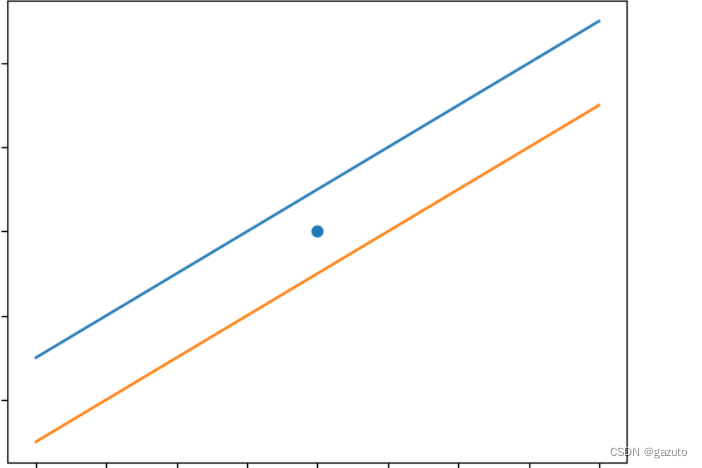
这表明要想训出来的直线接近真实值,接近的方向并不是唯一的不变的,而是非常的复杂
所以我们不能直接设定一个方向
而是要使用数学推导化繁为简
线性回归中,我们的目的是要找出最佳的,形如wx+b的直线,
其中x是我们的输入,那实际上我们就是要训练得出最佳的w,b参数
反过来说,如果有误差,那一定也来源于他们两个
所以我们的误差函数可以写成
l
o
s
s
i
(
w
,
b
)
=
1
2
(
z
i
−
y
i
)
2
loss_i(w,b) = \frac{1}{2} (z_i-y_i)^2
lossi(w,b)=21(zi−yi)2
现在来让我们考虑一个简单的例子
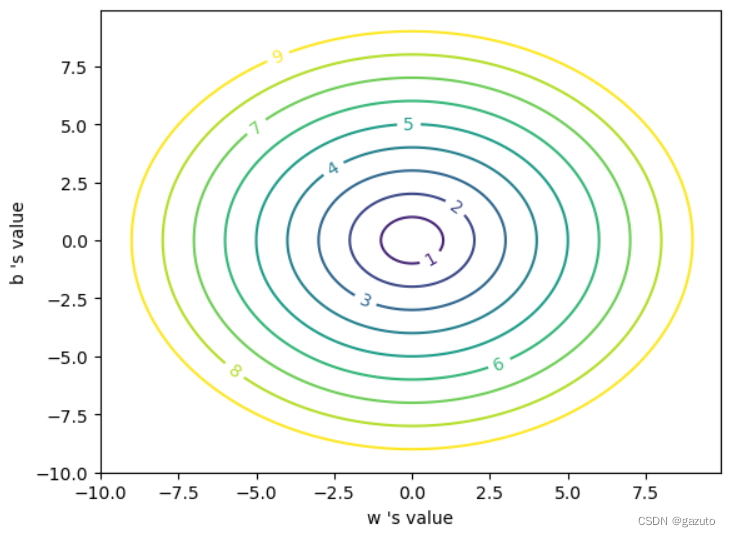
我们的误差函数由两个变量影响,所以可能是下面这样子的
即参数不同的取值的误差也许是相同的,从而构成一条条等值线
比如y=2x+1和y=2x+7对于点(0,4)的误差可能是相同的
那在这幅图上,(2,1)和(2,7)在同一条等值线上
为了方便探讨,我这里画成同心圆,现实问题可能更为复杂
我们希望得到一个方向,一个只要往那边走,无论如何总是能够减小误差的方向
真的会有这么方便好用的东西吗?
有的
这个方向就是梯度
准确的说,是==梯度向量指向的方向==
梯度向量,每个分量都是某个自变量各自的偏导数的向量
比如一个x,y作为自变量的函数,一般写成f(x,y)
则它的导数就是
∇
f
(
x
,
y
)
=
(
f
′
(
x
)
x
,
f
′
(
x
)
y
)
\nabla f(x,y) =(f'(x)_x , f'(x)_y)
∇f(x,y)=(f′(x)x,f′(x)y)
对于一个单变量函数
f
(
x
)
f(x)
f(x),其梯度可以被理解为函数的导数
f
′
(
x
)
f'(x)
f′(x)。导数代表着函数在某一点处的变化率,即当
x
x
x 增加时函数值增量与
x
x
x 变化量之比,也可以被看作是函数在该点处的切线的斜率。因此,函数在该点处的变化最快的方向即为导数的方向
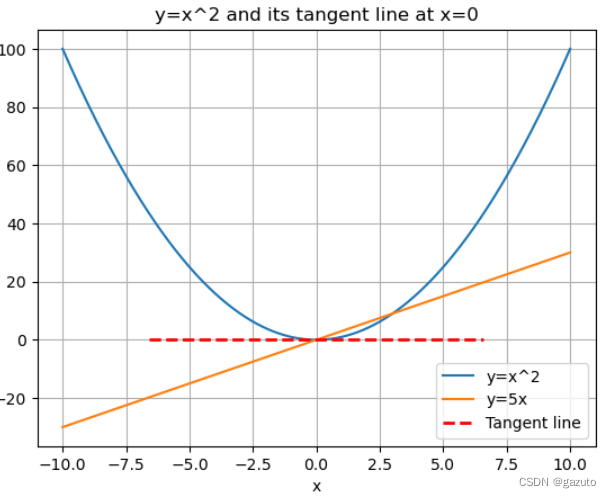
如上面x=0处的导数就是, f ′ ( 2 ) = 2 × 0 = 0 f'(2)=2 \times 0 = 0 f′(2)=2×0=0
x=2.5处的导数就是 f ′ ( 5 2 ) = 2 × 5 2 = 5 f'(\frac{5}{2})=2 \times \frac{5}{2} = 5 f′(25)=2×25=5
现在我们知道,函数在该点处的变化最快的方向即为导数的方向,而根据梯度定义,梯度向量在某点处的方向也指向函数值变化最快的方向。
如果我们沿着等值线移动一小段距离,函数值是不变的
换句话说,沿着等值线的方向移动时,函数值不变,因此函数在等值线上的方向上的变化率为零。
而梯度向量是函数在某点处变化最快的方向
不沿着等值线方向的任何移动方向均会随着时间或者距离的增加改变函数值,而梯度向量是要最快的方向
因此梯度向量与等值线构成的圆所在的切线垂直。
在神经网络中,梯度下降是反向传播算法的一种常用优化方法。
这里是一个简单的例子,演示如何计算一个二元函数 f ( x , y ) = x 2 + 2 y f(x, y) = x^2 + 2y f(x,y)=x2+2y 在点 ( 1 , 3 ) (1, 3) (1,3) 处的梯度,其中 x x x 和 y y y 分别表示自变量:
f
(
x
,
y
)
=
x
2
+
2
y
f(x, y) = x^2 + 2y
f(x,y)=x2+2y
∂
f
∂
x
=
2
x
\frac{\partial f}{\partial x} = 2x
∂x∂f=2x
∂
f
∂
y
=
2
\frac{\partial f}{\partial y} = 2
∂y∂f=2
函数 f ( x , y ) f(x, y) f(x,y) 在点 ( 1 , 3 ) (1, 3) (1,3) 处的梯度为:
∇ f ( 1 , 3 ) = [ ∂ f ∂ x ( 1 , 3 ) ∂ f ∂ y ( 1 , 3 ) ] = [ 2 ( 1 ) 2 ] = [ 2 2 ] T \nabla f(1, 3) = \begin{bmatrix}\frac{\partial f}{\partial x}(1, 3) & \frac{\partial f}{\partial y}(1, 3)\end{bmatrix} = \begin{bmatrix}2(1) & 2\end{bmatrix} = \begin{bmatrix}2 & 2\end{bmatrix}^T ∇f(1,3)=[∂x∂f(1,3)∂y∂f(1,3)]=[2(1)2]=[22]T
现在梯度对于我们来说应该不可怕了
(我知道数学推导很难熬,我写的时候也很煎熬qwq)
(实践部分)
下面来计算我们的项目要用到的梯度:
线性函数:
z
i
=
x
i
⋅
w
+
b
(1)
z_i = x_i \cdot w + b \tag{1}
zi=xi⋅w+b(1)
这是我们的损失函数:
(下标i表示其中一个样本)
l o s s i ( w , b ) = 1 2 ( z i − y i ) 2 (2) loss_i(w,b) = \frac{1}{2} (z_i-y_i)^2 \tag{2} lossi(w,b)=21(zi−yi)2(2)
计算z的梯度
根据公式2:
∂ l o s s ∂ z i = z i − y i (3) \frac{\partial loss}{\partial z_i}=z_i - y_i \tag{3} ∂zi∂loss=zi−yi(3)
计算 w w w 的梯度
我们用 l o s s loss loss 的值作为误差衡量标准,通过求 w w w 对它的影响,也就是 l o s s loss loss 对 w w w 的偏导数,来得到 w w w 的梯度。由于 l o s s loss loss 是通过公式2->公式1间接地联系到 w w w 的,所以我们使用链式求导法则,通过单个样本来求导。
根据公式1和公式3:
∂ l o s s ∂ w = ∂ l o s s ∂ z i ∂ z i ∂ w = ( z i − y i ) x i (4) \frac{\partial{loss}}{\partial{w}} = \frac{\partial{loss}}{\partial{z_i}}\frac{\partial{z_i}}{\partial{w}}=(z_i-y_i)x_i \tag{4} ∂w∂loss=∂zi∂loss∂w∂zi=(zi−yi)xi(4)
计算 b b b 的梯度
∂ l o s s ∂ b = ∂ l o s s ∂ z i ∂ z i ∂ b = z i − y i (5) \frac{\partial{loss}}{\partial{b}} = \frac{\partial{loss}}{\partial{z_i}}\frac{\partial{z_i}}{\partial{b}}=z_i-y_i \tag{5} ∂b∂loss=∂zi∂loss∂b∂zi=zi−yi(5)
用代码表示出来最后结果就是这样子
def __backward(self, x,y,z):
dz = z - y
db = dz
dw = x * dz
return dw, db
dz是中间变量,避免重复计算。dz又可以写成delta_Z,是当前层神经网络的反向误差输入。
这些算出来就是我们想要的w、b需要如何变动(朝哪个方向)才能得到真实值,可以直接使用这些值做更新
总结
以上就是今天要讲的内容,本文是该系列的第一篇,接下来的内容会写成额外的文章




















 1337
1337











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








