多元线性回归哑变量设置方法

多元线性回归是研究一个连续型变量和其他多个变量间线性关系的统计学分析方法，如果在自变量中存在分类变量，如果直接将分类变量和连续性变量统一纳入模型进行分析是有问题的，尤其是无序分类资料，即使进入了模型，也难以解释，因此分类资料纳入模型最佳的方式是设置哑变量。

在SPSS软件中，做Logistic回归时，直接有选项可以将分类变量设置哑变量，但是在做多元线性回归时，分析过程中没有设置哑变量的选项，就需要对原始数据进行拆解，将分类变量拆解成哑变量的形式。（值得一提的是，如果应变量能够转化为二分类的变量，直接采用Logistic回归分析也可以直接分析）

下面介绍在SPSS软件中多元线性回归哑变量设置的方法

以模拟的脑卒中患者康复期生活质量影响因素分析的数据为例，脑卒中患者的生活质量采用卒中专门生存质量量表（SS-QOL）来体现，SS-QOL评分是一个连续性资料，其分数越高，生存质量越好，为探究其影响因素，纳入以下一些研究变量：年龄、婚姻状况、文化程度、职业、BI评分。下图是数据格式，可以看出婚姻状况、文化程度、职业是分类资料。

从变量的赋值来看，这三个分类资料是无序分类资料，分析时，需要设置哑变量。下面介绍哑变量设置的方法。

第一步 SPSS菜单栏中 转换-创建虚变量

第二步 选择分类变量，将其放入“针对下列变量创建虚变量”框里，再重新命名哑变量的名称

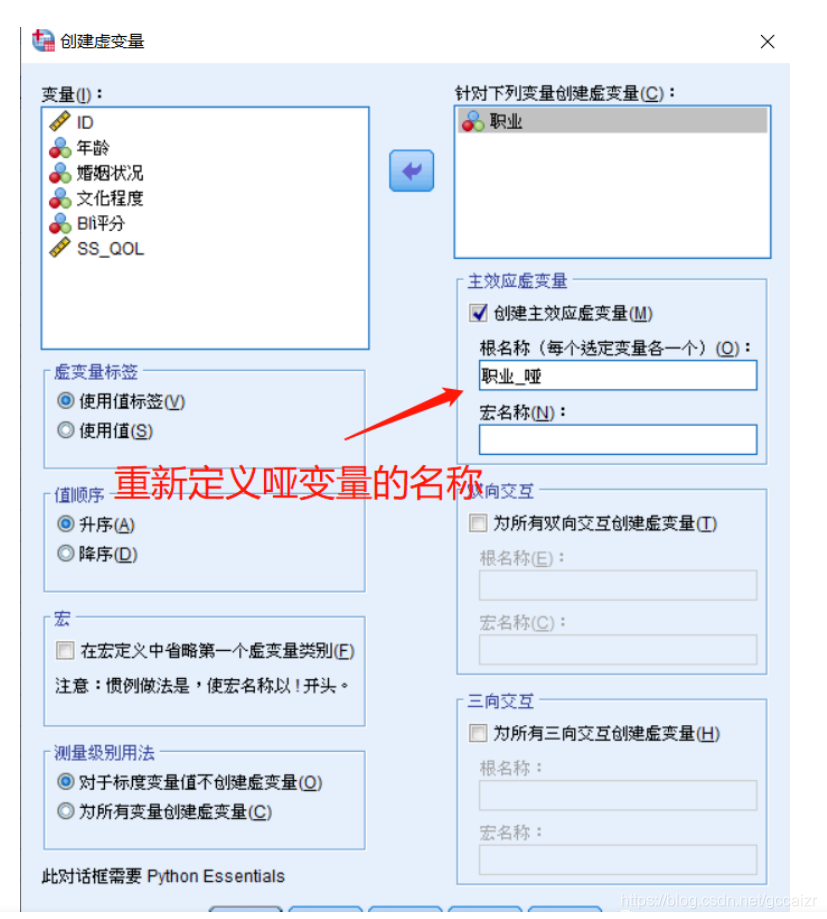
即可在数据中看到创建的哑变量，职业有4种分类，因此创建了4个哑变量

按照同样的方法，将其他分类变量创建哑变量

第三步 进行多元线性回归分析

第四步 哑变量选择

这里注意的是，分类变量的哑变量中确定一个参照变量，然后将除参考变量以外的其他哑变量同时放入自变量框中，如下图所示，把职业=0的做为参照，其他3个哑变量放入模型。

此外，由于哑变量要同出同进模型，因此方法必须选择“输入”

设置好一个哑变量后点“下一个”设置另一个哑变量

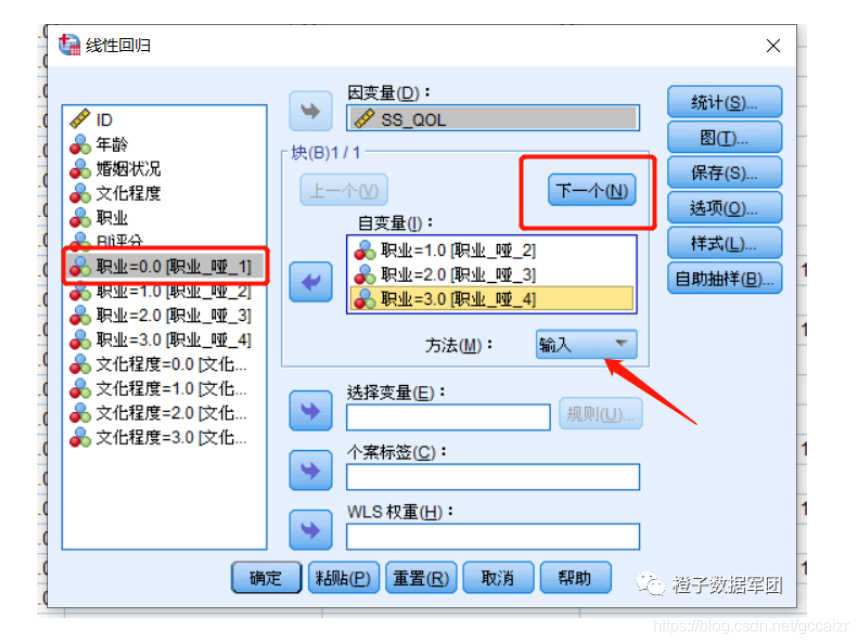
以此类推，先把所有分类变量设置好

第五步 放置其余变量

这个时候，其他的变量进入模型的方法就可以自由选择了，可以选择逐步，也可以选择其他。

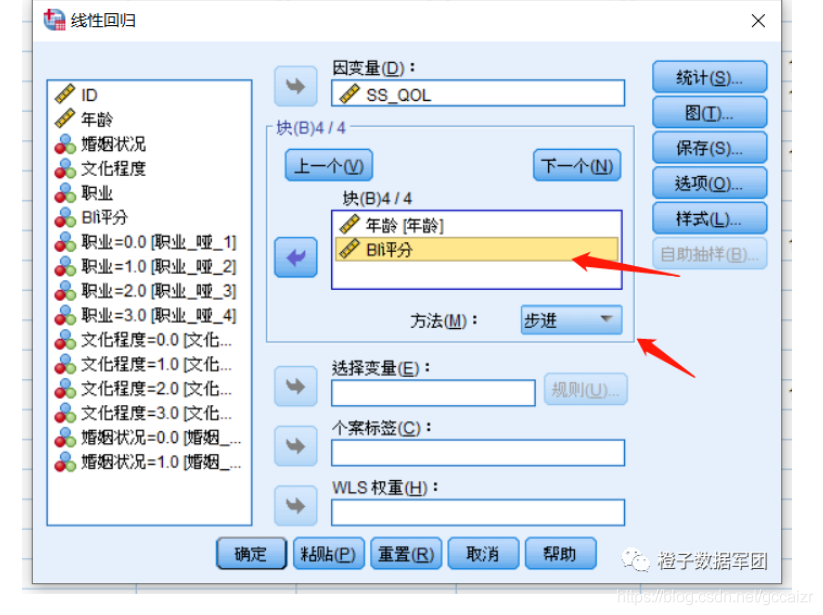
以上就是多元线性回归哑变量的设置方法。即使解决了哑变量的设置问题，在多元线性回归中，由于哑变量要同进同出，如果有多个分类变量的话，这些多分类是用软件没有办法来进行逐步回归，只能手动选择分类变量进入模型，多次比较模型效果来确定，此外，哑变量的参照组选择不同，对模型结果也是有影响，因此在设置参照哑变量时，可以进行多次尝试，选择对模型解释最佳的参照哑变量。
获取详细教学视频及粉丝交流群，请关注微信公众号【橙子数据军团】