作业要求: 对数据文件Knapsack.txt (第一行为背包总重量15,物品数量5;第2-6行,分别为第1-5件物品的重量与价值,W=15) , 编程计算最终背包所装物品的编号、总重量与总价值。要求能够把构造的二维表格输出到文件KnapsackResult.txt中。
数据文件内容:
单副本的背包问题(Knapsack without repetition):N件物品,分别重w1,...,wn,价值为v1,...,vn,现有一个背包最大容量为W,怎样的组合才能够使背包中装下的物品价值最高?
摘自: knapsack-problem(http://www.answers.com/topic/knapsack-problem)
单副本背包问题的伪代码:
用Java实现单副本背包问题,代码如下:
/**
* 单副本背包问题
*/
public class Knapsack {
/**
* 计算背包问题的二维表格
* @param W 背包可容纳的最大重量
* @param n 物品数量
* @param K 二维表格
* @param wv wv[i][0]=w(该物品的重量) , wv[i][1]=v(该物品的价值) , 0<=i<=n
*/
public int[][] getArray(int W, int n, int wv[][]){
//第一行和第一列的所有值为0
int[][] K = new int[W+1][n+1];
//核心代码的实现,参照伪代码
for(int j=1; j<=n; j++){
for(int w=1; w<=W; w++){
int maxW = wv[j-1][0];
if(maxW>w){
K[w][j] = K[w][j-1];
}else{
K[w][j] = max(K[w][j - 1],K[w - maxW][j - 1]+wv[j - 1][1]);
}
}
}
return K;
}
public int max(int a, int b){
return a>b ? a : b;
}
/**
* 计算放入背包中的物品总质量和哪些物品放到背包中
* @param wv wv[i][0]=w(该物品的重量) , wv[i][1]=v(该物品的价值) , 0<=i<=n
* @param K 存储背包问题的二维数组
* @param W 背包可容纳的最大重量
* @param n 物品数量
* @return isTaked[] 第一个位置放
*/
public static int[] getIsTaked(int[][] wv,int[][] K,int W,int n){
/* 下标为0的数组值存储放到背包里的物品总价值
从下标1开始记录该物品编号是否放入背包中(下标即为物品的编号),
1是放入,0是不放入 */
int isTaked[]=new int[n+1];
int w = W;
for(int j=n;j>0;j--){
if(K[w][j]>K[w][j-1]){
isTaked[j]=1;
w = w - wv[j-1][0];
if(w<0) break;
}
}
//计算放入背包的物品总重量
int sumW=0;
for(int j=1;j<=n;j++){
if(isTaked[j]==1){
sumW+=wv[j-1][0];
}
}
isTaked[0] = sumW;
return isTaked;
}
}测试代码:
public static void main(String[] args) throws IOException {
Scanner scanner = new Scanner(Knapsack.class.getResourceAsStream("Knapsack.txt"));
Writer out = new FileWriter(new File("src/KnapsackResult.txt"));
//第一行为背包总重量15,物品数量5
int W=scanner.nextInt(), n=scanner.nextInt();
//将每个物品的重量和价值保存到数组wv
int wv[][] = new int[n][2];
for(int i=0; i<n; i++){
wv[i][0]=scanner.nextInt();
wv[i][1]=scanner.nextInt();
}
Knapsack knapsack = new Knapsack();
int K[][] = knapsack.getArray(W, n, wv);
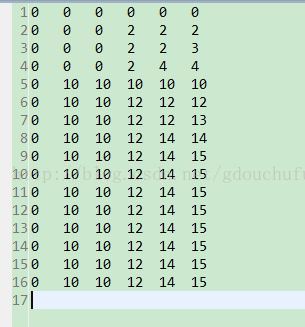
//将背包问题的二维表格保存到问文件KnapsackResult.txt
for(int w=0; w<=W; w++){
for(int j=0; j<=n; j++){
out.write(K[w][j]+"\t");
}
out.write("\r\n");
}
out.close();
scanner.close();
int[] isTaked = getIsTaked(wv, K, W, n);
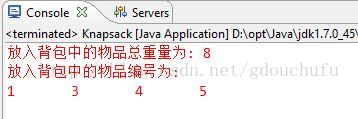
System.err.println("放入背包中的物品总重量为: "+isTaked[0]);
System.err.println("放入背包中的物品编号为: ");
for(int No=1; No<isTaked.length; No++){
if(isTaked[No] == 1) System.err.print(No + "\t");
}
}测试结果:










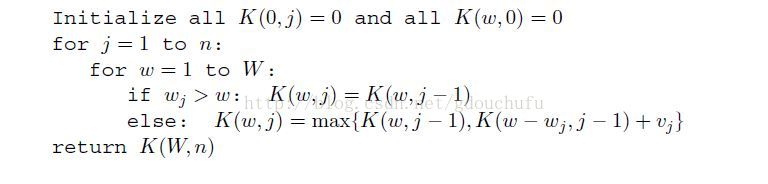














 1835
1835

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








