1-1 Course Introduction
- 课程网址连接:
- Coursera:没找到
- Bilibili:https://www.bilibili.com/video/av12469267
1-2 Large-Margin Separating Hyperplane
回顾一下linear classification,对于线性可分的情况,我们可以使用PLA/pocket算法在平面或者超平面上把正负类分开
例如对平面2D这种情况,我们可以找到一条直线,能将正类和负类完全分开

单从分类效果上看,上面的三条直线都满足要求,而且都满足VC bound要求,模型复杂度是一样的,即具有一定的泛化能力。但是,正常人凭第一感觉还是会选择第三条直线,直观上会感觉它的分类效果更好一些。那这又是为什么呢?
我们知道,一般情况下,训练样本外的测量数据应该分布在训练样本附近,但与训练样本的位置有一些偏差
若要保证对未知的测量数据也能进行正确分类,最好让分类直线距离正类负类的点都有一定的距离。这样能让每个样本点附近的圆形区域是“安全”的。圆形区域越大,表示分类直线对测量数据误差的容忍性越高,越“安全”

如上图所示,左边的点距离分类直线的最小距离很小,它的圆形区域很小。那么,这种情况下,分类线对测量数据误差的容忍性就很差,测量数据与样本数据稍有偏差,很有可能就被误分。而右边的点距离分类直线的最小距离更大一些,其圆形区域也比较大。这种情况下,分类线对测量数据误差的容忍性就相对来说大很多,不容易误分。
那么,如果每一笔训练资料距离分类线越远的话,就表示分类型可以忍受更多的测量误差(noise)。
noise是造成overfitting的主要原因,而测量误差也是一种noise。所以,如果分类线对测量误差的容忍性越好的话,表示这是一条不错的分类线。那么,我们的目标就是找到这样一条最“健壮”的线,即距离数据点越远越好。

定义分类线的容忍度,就是看距离分类线最近的点与分类线的距离,我们把它用margin表示。分类线由权重w决定,目的就是找到使margin最大时对应的w值。整体来说,我们的目标就是找到这样的分类线并满足下列条件
- 分类正确,即
- margin最大化

1-3 Standard LargeMargin Problem
如何计算点到分类线的距离?
首先,我们将权重中的
拿出来,用b表示。同时省去
项。这样,hypothesis就变成了

下面,利用图解的方式,详细推导如何计算点到分类平面的距离:

如上图所示,平面上有两个点:x'和x''。因为这两个点都在分类平面上,所以它们都满足:
同时可以得到:,则有:
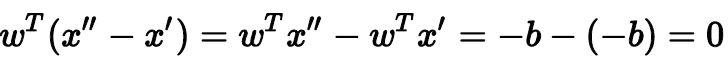
(x'',x')是平面上的任一向量,(x'',x')与w内积为0,表示(x'',x')垂直于w,那么w就是平面的法向量。现在,若要计算平面外一点x到该平面的距离,做法是只要将向量(x,x')投影到垂直于该平面的方向(即w方向)上就可以了。那么,令(x'',x')与w的夹角为,距离就可以表示为:
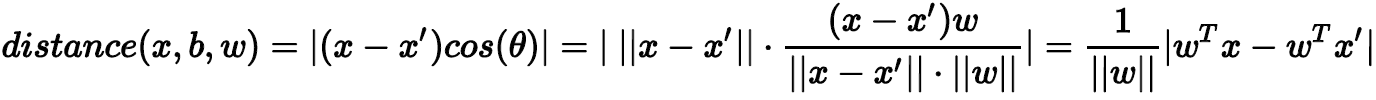
代入,可得:
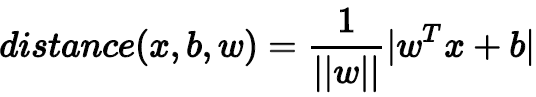
点到分类面(Separating Hyperplane)的距离已经算出来了。基于这个分类面,所有的点均满足:,表示所有点都分类正确,则distance公式就可以变换成:
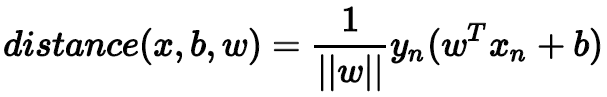
那么,我们的目标形式就转换为:
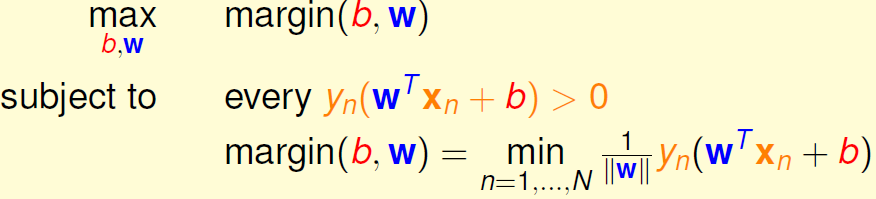
对上面的式子还不容易求解,我们继续对它进行简化。我们知道分类面和
其实是一样的。也就是说,对w和b进行同样的缩放还会得到同一分类面。所以,为了简化计算,我们令距离分类满最近的点满足
。那我们所要求的margin就变成了:

这样,目标形式就简化为:
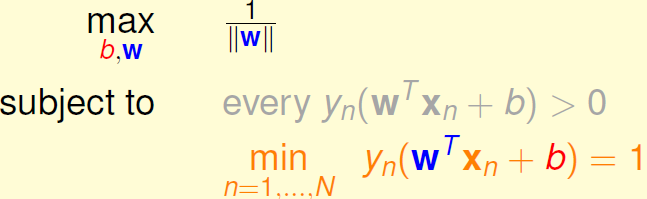
这里可以省略条件: ,因为满足条件
必然满足大于零的条件。我们的目标就是根据这个条件,计算
的最大值。
刚刚我们讲的距离分类满最近的点满足,也就是说对所有的点满足
。另外,因为最小化问题我们最熟悉也最好解,所以可以把目标
最大化转化为计算
的最小化问题。

如上图所示,最终的条件就是,而我们的目标就是最小化
值。
1-4 Support Vector Machine
现在,条件和目标变成:
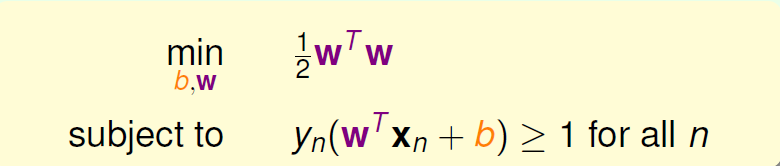
现在,举个例子,假如平面上有四个点,两个正类,两个负类:

不同点的坐标加上条件,可以得到:

最终,我们得到的条件是:
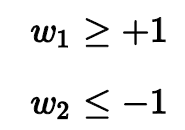
而我们的目标是:
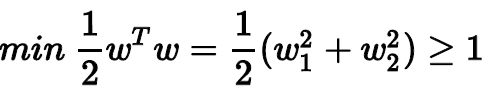
目标最小值为1,即,那么这个例子就得到了最佳分类面的解,如图所示,且
。分类面的表达式为:

最终我们得到的矩的表达式为:
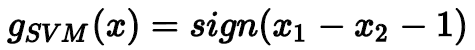
Support Vector Machine(SVM)这个名字从何而来?为什么把这种分类面解法称为支持向量机呢?这是因为分类面仅仅由分类面的两边距离它最近的几个点决定的,其它点对分类面没有影响。决定分类面的几个点称之为支持向量(Support Vector),好比这些点“支撑”着分类面。而利用Support Vector得到最佳分类面的方法,称之为支持向量机(Support Vector Machine)。
下面介绍SVM的一般求解方法。先写下我们的条件和目标:
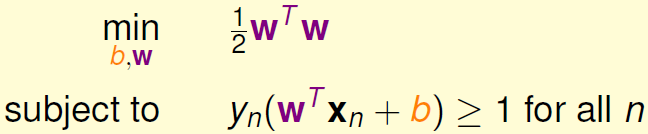
这是一个典型的二次规划问题,即Quadratic Programming(QP)。因为SVM的目标是关于w的二次函数,条件是关于w和b的一次函数,所以,它的求解过程还是比较容易的,可以使用一些软件(例如Matlab)自带的二次规划的库函数来求解。下图给出SVM与标准二次规划问题的参数对应关系:

那么,线性SVM算法可以总结为三步:
- 计算对应的二次规划参数Q,p,A,c
- 根据二次规划库函数,计算b,w
- 将b和w代入,得到最佳分类面
这种方法称为Linear HardMargin SVM Algorithm。如果是非线性的,例如包含x的高阶项,那么可以使用我们之前在《机器学习基石》课程中介绍的特征转换的方法,先作的特征变换,从非线性的x域映射到线性的z域空间,再利用Linear HardMargin SVM Algorithm求解即可。
1-5 Reasons behind LargeMargin Hyperplane






















 958
958











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








