1 概述
图（Graph）是由顶点的有穷非空集合，和顶点之间边的集合组成，通常表示为：G(V, E)，其中，G表示一个图，V是图G中顶点的集合，E是图G中边的集合。
线性表中，每个数据元素只有一个直接前驱和一个直接后继；树中，每一层上的数据元素可能和下一层的多个数据元素相连，但只能和上一层的一个数据元素相连；图则不一样，结点之间的关系可以是任意的，图中任意两个元素都可以相连。
对于图的定义，还有以下需要注意的点：
(1) 线性表的数据元素称为元素，树中的数据元素称为结点，而图中的数据元素被称为顶点（Vertex）；
(2) 线性表可以没有数据元素，称为空表；树可以没有结点，称为空树；但在图中，不允许没有顶点；
(3) 线性表中，相邻的数据元素之间具有线性关系；树中，相邻两层的结点有层次关系；但在图中，任意两个顶点之间都可能有关系，顶点之间的逻辑关系用边来表示，边集可以是空的；
1.1 无向和有向
若顶点Vi到Vj之间的边没有方向，则称这条边为无向边（Edge），如果图中的所有边都是无向边，则该图称为无向图（Undirected graphs）。
下图即为一个无向图：
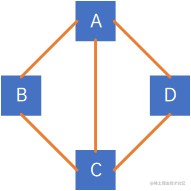
由于是无方向的，因此连接顶点A与D的边，可以表示成(A,D)，也可以表示成(D,A)。
顶点集合V={A,B,C,D}，边集合也没有顺序，可以表示为E={(A,B), (B,C), (C,D), (D, A), (A,C)}，当然，因为是无序的，所以边集合里面的字母和边集也可以任意调换顺序。
该图则表示为G=({A,B,C,D}, {(A,B), (B,C), (C,D), (D, A), (A,C)})。
若顶点Vi到Vj之间的边有方向，则称这条边为有向边（Edge），也称为弧（Arc），如果图中的所有边都是有向边，则该图称为有向图（Directed graphs）。
下图即为一个有向图：
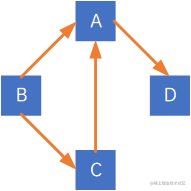
有向边的箭头尾部的顶点称为弧尾，箭头头部的顶点称为弧头，有向边的边集只能写成<弧尾,弧头>，一定要用尖括号，且顺序不能乱，如上图，顶点A和顶点D之间的边是有向边，A是弧尾，D是弧头，因此边集只能表示为<A,D>。
顶点集合V={A,B,C,D}，边集合则为E={<A,D>, <B,A>, <C,A>, <B,C>}，因此上图表示为G=({A,B,C,D}, {<A,D>, <B,A>, <C,A>, <B,C>})。
1.2 各种图的定义
在图中，若不存在顶点到其他自身的边，且同一条边不重复出现，则称这样的图为简单图。
以下两个图，则不为简单图：
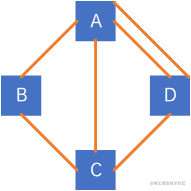
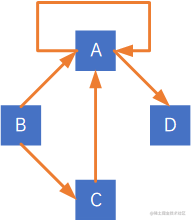
在无向图中，如果任意两个顶点之间都存在边，则称该图为无向完全图，含有n个顶点的无向完全图有 n ∗ ( n − 1 ) ÷ 2 n * (n-1) \div 2 n∗(n−1)÷2条边，下图为一个无向完全图：
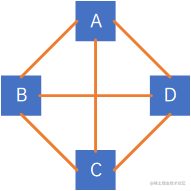
因此，对于具有n个结点和e条边的无向图，0 ≤ e ≤ n * (n - 1) /2。
在有向图中，如果任意两个顶点之间都存在方向互为相反的两条弧，则称该图为有向完全图，含有n个顶点的有向完全图有 n ∗ ( n − 1 ) n \ast (n-1) n∗(n−1)条边，如下图所示：
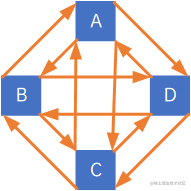
因此，对于具有n个结点和e条边的有向图，0 ≤ e ≤ n * (n - 1)。
有很少条边或弧的图称为稀疏图，反之称为稠密图。
有些边或弧具有与它相关的数字，这种与图的边或弧相关的数叫权（Weight），这种带权的图称为网（Network），如下图所示：
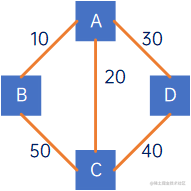
假设有两个图G=(V,E)和G’=(V’,E’)，如果 V ′ ⊆ V V' \subseteq V V′⊆V且 E ′ ⊆ E E' \subseteq E E′⊆E，则称图G’为图G的子图（Subgraph），如下，图1为图2的子图：
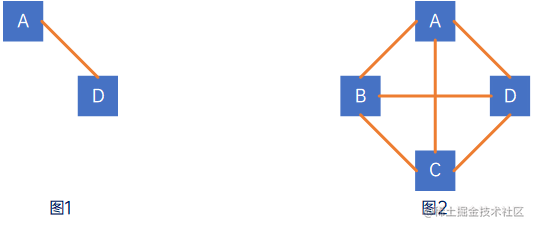
1.3 图的顶点与边间的关系
对于无向图，被一条边连接的两个顶点互为邻接点（Adjacent），连接这两个顶点的边则依附（incident）于这两个顶点，或者称边与这两个顶点相关联，与顶点相关联的边的数量称为顶点的度（Degree），一般计为TD(v)，而边的数量，其实就是各顶点度数和的一半（多出的一半是因为重复两次记数），即 e = 1 2 ∑ i = 1 n T D ( v i ) e= \frac{1}{2} \sum^{n}_{i=1}TD(v_i) e=21∑i=1nTD(vi)。
以下图为例：
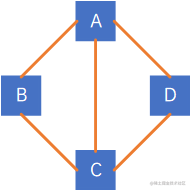
顶点A和B互为邻接点，边(A,B)依附于顶点A和顶点B，边(A,B)与顶点A相关联也与顶点B相关联，A的度为3，B的度为2，C的度为3，D的度为2，图的边 E = ( 3 + 2 + 3 + 2 ) ÷ 2 = 5 E=(3+2+3+2) \div 2 = 5 E=(3+2+3+2)÷2=5。
对于有向图，如果存在弧<v,v’>，则称顶点v邻接到v’，顶点v’邻接自v，弧<v,v’>与顶点v和v’相关联，以顶点v为头的弧的数目称为v的入度（InDegree），记为ID；以顶点v为尾的弧的数目称为v的出度（OutDegree），记为OD，顶点v的度为 T D ( v ) = I D ( v ) + O D ( v ) TD(v)=ID(v)+OD(v) TD(v)=ID(v)+OD(v)，有向图的边的数量与各顶点的入度和相等，也与各顶点的出度和相等，即 e = ∑ i − 1 n I D ( v i ) = ∑ i − 1 n O D ( v i ) e= \sum^{n}_{i-1}ID(v_i) = \sum^{n}_{i-1}OD(v_i) e=∑i−1nID(vi)=∑i−1nOD(vi)。
以以下有向图为例：
存在弧<B,A>，因此称顶点B邻接到顶点A，顶点A邻接自顶点B，弧<B,A>与顶点A、B相关联，顶点A的入度为2，出度为1，顶点B的入度为0，出度为2，顶点C的入度为1，出度为1，顶点D的入度为1，出度为0，边的数量 e = 入度和 = 2 + 0 + 1 + 1 = 出度和 = 1 + 2 + 1 + 0 = 4 e=入度和=2+0+1+1=出度和=1+2+1+0=4 e=入度和=2+0+1+1=出度和=1+2+1+0=4。
从顶点v到顶点v’的路径（Path）是一个顶点序列 ( v = v i , 0 , v i , 1 , v i , 2 . . . . . . v i , m = v ′ ) (v=v_{i,0},v_{i,1},v_{i,2}......v_{i,m}=v') (v=vi,0,vi,1,vi,2......vi,m=v′)，其中 ( v i , j − 1 , v i , j ) ∈ E (v_{i,j-1},v_{i,j}) \in E (vi,j−1,vi,j)∈E， 1 ≤ j ≤ m 1 \leq j \leq m 1≤j≤m，当然，对于有向图是$ <v_{i,j-1},v_{i,j}> \in E$， 1 ≤ j ≤ m 1 \leq j \leq m 1≤j≤m。
如下无向图，顶点B到顶点D的路径有：
分别表示为B=(B,A,D)=D，B=(B,C,D)=D，B=(B,A,C,D)=D和B=(B,C,A,D)=D。
如下有向图，顶点B到顶点D的路径有：
分别表示为B=(B,A,D)=D和B=(B,C,A,D)=D。
路径的长度是路径上的边或弧的数目。
第一个顶点到最后一个顶点相同的路径称为回路或环（Cycle，在离散数据中，自己连自己称为环），序列中顶点不重复出现的路径称为简单路径，除了第一个顶点和最后一个顶点之外，其余顶点不重复出现的回路，称为简单回路或简单环。
如下图：
路径A=(A,B,C,D)=D中，顶点没有重复出现，因此是一个简单路径，但路径A=(A,B,C,A,D)=D，A有重复出现，因此不是简单路径。
路径A=(A,B,C,D,A)=A，从A回到了A，且除头和尾顶点外，其他顶点没有重复，因此是回路，而且是简单回路。路径A=(A,B,C,D,C,A)=A，从A回到了A，是回路，但因为除头和尾外，C也重复了，因此不是简单回路。
1.4 连通图
在无向图G中，如果从顶点v到顶点v’有路径，则称v和v’是连通的，如果对于图中任意两个顶点 v i , v j ∈ E v_i,v_j \in E vi,vj∈E， v i v_i vi和 v j v_j vj都是连通的，则称G是连通图（Connected Graph），下图中的左图顶点A和顶点B是连通的，但左图不是连通图，因为A到E和F都没有路径，下图中的右图则是连通图：
无向图中的极大连通子图称为连通分量，注意有几个条件：
(1) 要是子图；
(2) 子图要是连通的；
(3) 连通子图要含有极大顶点数，极大的意思不是最多，而不“不能再多”；
(4) 具有极大顶点数的连通子图要包含依附于这些顶点的所有边；
如下图是一个无向非连通图：
它有两个连通分量：
注意看，这两个连通分量都是连通图，且不能再纳入其他顶点，因此称为“极大”。
如果图G是一个连通图，把它去掉一个边后，形成的子图仍是连通图，且边的数量为顶点数量n-1，则称该生成的子图G’为连通图G的生成树。
下图是一棵连通图：
去掉一条边后的下面两个子图是连通图的生成树：
但去掉一个边后，形成的子图不是连通图的情况，则不是连通图的生成树，如下图：
如果一个有向图恰巧有一个顶点的入度为0，其余顶点的入度均为1，则是一棵有向树。一个有向图生成的有向树集合，称为有向图的有向森林，下图是一个有向图：
以下两个图是该图的所有有向树，它们组成了该图的有向森林：
2 图的抽象数据类型
图作为一种数据结构，也有图的抽象数据类型，如下：
3 图有存储结构
3.1 邻接矩阵
图的邻接矩阵（Adjacency Matrix）存储方式是用两个数组来表示图，一个一维数据存储图中顶点信息，一个二维数组（称为邻接矩阵）存储图中的边或弧的信息。
设图G有n个顶点，则邻接矩阵是一个
n
×
n
n \times n
n×n的方阵，定义为：
a
r
c
[
i
]
[
j
]
=
{
1
,
若
(
v
i
,
v
j
)
∈
E
或
<
v
i
,
v
j
>
∈
E
0
，反之
arc[i][j] = \begin{cases}1,若(v_i,v_j) \in E 或 <v_i,v_j> \in E\\0，反之\end{cases}
arc[i][j]={1,若(vi,vj)∈E或<vi,vj>∈E0，反之
以以下无向图为例：
先建一个一维数组，来存储顶点，如vertex[4]={D,A,C,B}，然后知道vertex[0]=“D”，vertex[1]=“A”，vertex[2]=“C”，vertex[3]=“B”。现在来建一个二维数组arc[4][4]，用于存储边，其中arc[i][j]为顶点i到顶点j之间是否有边，有则值为1，无则值为0，例如，顶点0到顶点0即vertex[0]到vertex[0]，是同一个顶点D，它们之间没有边，因此arc[0][0]=0，顶点2到顶点1即vertex[2]到vertex[1]即顶点C到顶点A之间是有边的，因此arc[2][1]=1，于是得到以下矩阵：
从上图可知，无向图的边数组是一个对称矩阵，从这个矩阵中可以简单地获知：
(1) 两个顶点之间是否有边，看arc[i][j]是否为1即可；
(2) 某个顶点的度，为
D
(
i
)
=
∑
j
,
0
≤
j
≤
n
n
a
r
c
[
i
]
[
j
]
D(i)=\sum^n_{j,0 \leq j \leq n}arc[i][j]
D(i)=∑j,0≤j≤nnarc[i][j]，即arc[i][0]+arc[i][1]+arc[i][2]…+arc[i][n]，当然，因为是对称矩阵，所以也可以是
D
(
i
)
=
∑
j
,
0
≤
j
≤
n
n
a
r
c
[
j
]
[
i
]
D(i)=\sum^n_{j,0 \leq j \leq n}arc[j][i]
D(i)=∑j,0≤j≤nnarc[j][i]，即arc[0][i]+arc[1][i]+arc[2][i]…+arc[n][i]；
(3) 求顶点
V
i
V_i
Vi的所有邻接点，就是将矩阵中第i行元素扫描一遍，arc[i][j]为1就是邻接点；
再看以下有向图：
仍然建一个数组vertex[4]={D,A,C,B}来存储顶点，用arc[4][4]来存储弧，若有弧则值为1，若无弧则值为0，形成如下矩阵：
主对角线上数值依然是0，但因为是有向图，因此矩阵并不对称，arc[i][j]表示顶点vertex[i]到vertex[j]是否有弧，有为1，无为0，求邻接点的方式仍然一样，但因为有向图是入度和出度，因此度的算法有所变化：
(1) 求出度，数量为OD[i]=arc[i][0] + arc[i][1] + … + arc[i][n]，即
∑
j
,
0
≤
j
≤
n
n
a
r
c
[
i
]
[
j
]
\sum^n_{j, 0 \leq j \leq n}arc[i][j]
∑j,0≤j≤nnarc[i][j];
(2) 求入度，数量为ID[i]=arc[0][i] + arc[1][i] + … + arc[n][i]，即
∑
j
,
0
≤
j
≤
n
n
a
r
c
[
j
]
[
i
]
\sum^n_{j, 0 \leq j \leq n}arc[j][i]
∑j,0≤j≤nnarc[j][i];
除无向图和有向图外，还有网图，这时边或弧矩阵值的算法为：
a
r
c
[
i
]
[
j
]
=
{
W
i
j
，若
(
v
i
,
v
j
)
∈
E
或
<
v
i
,
v
j
>
∈
E
0
，若
i
=
j
∞
，反之
arc[i][j]=\begin{cases} {W_{ij}}，若(v_i,v_j) \in E 或<v_i,v_j> \in E \\ 0，若i = j \\ \infty，反之 \end{cases}
arc[i][j]=⎩
⎨
⎧Wij，若(vi,vj)∈E或<vi,vj>∈E0，若i=j∞，反之
即若有边或弧，则arc[i][j]为权值，若i=j，则arc[i][j]=0，否则是一个无穷大的值。
来看如下网图：
先定义顶点数组vertex[4]={D,A,C,B}，然后按照规则，生成以下矩阵arc：
度的算法不再是判断是否为1，而是
D
(
i
)
=
∑
j
,
0
≤
j
≤
n
n
a
r
c
[
i
]
[
j
]
D(i) = \sum ^n_{j,0 \leq j \leq n} arc[i][j]
D(i)=∑j,0≤j≤nnarc[i][j]，且
a
r
c
[
i
]
[
j
]
=
{
∞
,
0
i
=
j
,
0
1
arc[i][j] = \begin{cases} \infty,0 \\ i=j,0 \\ 1 \end{cases}
arc[i][j]=⎩
⎨
⎧∞,0i=j,01，即若arc[i][j]为无穷大或者i=j时，表示不相关，否则表示相关。
对于有向网图的入度和出度算法类似。
邻接矩阵的创建比较简单，只需要输入顶点数组和边或弧数组即可：
/**
* 按照顶点集vertex和边弧集arc定义构建图
* <p>
* 有向图和有向网图的弧的数量，是arc中，arc[i][j]的i!=j，且arc[i][j]!=infinity的元素的数量
* <p>
* 无向图和无向网图的边的数量，是arc中，arc[i][j]的i!=j，且arc[i][j]!=infinity的元素的数量的一半
*
* @param vertex 顶点集
* @param arc 边或弧矩阵
* @param type 图类型
* @author Korbin
* @date 2023-01-31 14:23:07
**/
public void create(T[] vertex, W[][] arc, int type) {
this.vertex = vertex;
this.arc = arc;
this.vertexNum = vertex.length;
this.type = type;
// 有向图的弧的数量，是arc中，arc[i][j]的i!=j，且arc[i][j]!=infinity的元素的数量
// 无向图的边的数量，是arc中，arc[i][j]的i!=j，且arc[i][j]!=infinity的元素的数量的一半
int edgeNumTmp = 0;
for (int i = 0; i < arc.length; i++) {
for (int j = 0; j < arc[i].length; j++) {
if (i != j && !arc[i][j].equals(infinity)) {
if (type == 1 || type == 2) {
// 对于无向图和有向图来说，如果矩阵值为0,也表示不相关联
try {
int arcValue = (Integer) arc[i][j];
if (arcValue != 0) {
edgeNumTmp++;
}
} catch (NumberFormatException e) {
// do nothing
}
} else {
// 对于无向网图和有向网图，只要矩阵值不为infinity，则表示相关
edgeNumTmp++;
}
}
}
}
if (type == 1 || type == 3) {
// 无向图和无向网图的边的数量，是arc中，arc[i][j]的i!=j，且arc[i][j]!=infinity的元素的数量的一半
this.edgeNum = edgeNumTmp / 2;
} else if (type == 2 || type == 4) {
// 有向图和有向网图的弧的数量，是arc中，arc[i][j]的i!=j，且arc[i][j]!=infinity的元素的数量
this.edgeNum = edgeNumTmp;
}
}
需要注意的是：
(1) 对于无向图和有向图来说，如果矩阵值为0,也表示不相关联；
(2) 无向图和无向网图的边的数量，是arc中，arc[i][j]的i!=j，且arc[i][j]!=infinity（在(1) 的基础上）的元素的数量的一半；
(3) 有向图和有向网图的弧的数量，是arc中，arc[i][j]的i!=j，且arc[i][j]!=infinity（在(1) 的基础上）的元素的数量；
使用类似如下方式调用create接口：
@Test
void create() {
// 无向图
String[] vertex = new String[]{"D", "A", "C", "B"};
Integer[][] arc = new Integer[][]{{0, 1, 1, 0}, {1, 0, 1, 1}, {1, 1, 0, 1}, {0, 1, 1, 0}};
graph.create(vertex, arc, 1);
Assertions.assertEquals(4, graph.getVertexNum());
Assertions.assertEquals(5, graph.getEdgeNum());
// 有向图
vertex = new String[]{"D", "A", "C", "B"};
arc = new Integer[][]{{0, 0, 0, 0}, {1, 0, 0, 0}, {0, 1, 0, 0}, {0, 1, 1, 0}};
graph.create(vertex, arc, 2);
Assertions.assertEquals(4, graph.getVertexNum());
Assertions.assertEquals(4, graph.getEdgeNum());
// 无向网图
vertex = new String[]{"D", "A", "C", "B"};
arc = new Integer[][]{{0, 30, 40, Integer.MAX_VALUE}, {30, 0, 20, 10}, {40, 20, 0, 0},
{Integer.MAX_VALUE, 10, 0, 0}};
graph.create(vertex, arc, 3);
Assertions.assertEquals(4, graph.getVertexNum());
Assertions.assertEquals(5, graph.getEdgeNum());
// 无向网图
vertex = new String[]{"D", "A", "C", "B"};
arc = new Integer[][]{{0, Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE},
{16, 0, Integer.MAX_VALUE, Integer.MAX_VALUE}, {Integer.MAX_VALUE, 17, 0, Integer.MAX_VALUE},
{Integer.MAX_VALUE, 15, 0, 0}};
graph.create(vertex, arc, 4);
Assertions.assertEquals(4, graph.getVertexNum());
Assertions.assertEquals(4, graph.getEdgeNum());
}
3.2 邻接表
但图是一个稀疏图时，使用邻接矩阵会存在大量的浪费，如下所示：
可以看到，在边或弧的矩阵中存在大量的$ \infty $，这种情况，我们可以把边或弧的矩阵使用单链表来存储，这种数组与链表结合的存储方式称为邻接表（Adjacency List）。
邻接表的处理方式是：
(1) 图中顶点用一个一维数组存储（当然，也可以选择单链表），顶点数组中的元素不仅存储着顶点信息，也存储着指向第一个邻接点的指针；
(2) 图中每个顶点Vi的所有邻接点构成一个线性表，由于邻接点的个数不定，所以用单链表存储，无向图称为顶点
v
i
v_i
vi的边表，有向图称为顶点
v
i
v_i
vi作为弧尾的出边表；
以以下无向图为例，先定义顶点数组vertex[4]={D,A,C,B}，然后按照规则，生成以下存储结构：
什么是第一个相邻点？我们以顶点C为例，它的相邻点有A、B、D，所谓第一个相邻点，是指在vertex中，下标或者位置排在最前面的那个相邻点，本图中，A的下标是1，B的下标是3，D的下标是0，那么，C的第一个相邻点就是下标为0的D。由图可知，无向图边的数量是所有单琏表结点数量和的一半。
对于有向图，建立邻接链的方法也是类似：
但有时为了便于确定顶点的入度或以顶点为弧头的弧，我们会建立一个有向图的逆邻接表，即对每个顶点 v i v_i vi都建立一个链接为 v i v_i vi为弧头的表，如下所示：
对于无向网或者有向网，则在边表或弧表中新增一个weight数据域表示权值即可：
由图可知，有向图边的数量是所有单琏表结点数量和。
邻接表的顶点结点结构只需要数据域和第一个邻接点对应的边或弧结点指针即可，如下所示：
import lombok.Data;
/**
* 顶点表结点
* <p>
* T表示顶点类型
* <p>
* W表示权值类型
*
* @author Korbin
* @date 2023-01-31 16:05:38
**/
@Data
public class VertexNode<T, W> {
/**
* 边表头指针，也即第一个邻接点的位置
**/
private EdgeNode<W> firstEdge;
/**
* 顶点
**/
private T vertex;
}
边或弧结点结构如下：
import lombok.Data;
/**
* 邻接表中边表或弧表的结点
* <p>
* W表示权值类型
*
* @author Korbin
* @date 2023-01-31 16:01:11
**/
@Data
public class EdgeNode<W> {
/**
* 该顶点对应的下标，该顶点实际上是某一个顶点的邻接点
**/
private int index;
/**
* 下一个邻接点
**/
private EdgeNode<W> next;
/**
* 权值
**/
private W weight;
/**
* 构造子
**/
public EdgeNode(int index, W weight) {
this.index = index;
this.weight = weight;
}
}
创建时只需要输入顶点值数组和边结点二维数组即可：
/**
* 按照顶点集值vertexValues和边或弧链表结点数组构造图
* <p>
* 无向图和无向网图的边的数量，是所有单链表结点的总数的一半
* <p>
* 有向图和有向网图的弧的数量，是所有单链表结点的总数的一半
*
* @param vertexValues 顶点集
* @param edges 边或弧矩阵，不存储next
* @param type 图类型
* @author Korbin
* @date 2023-01-31 14:23:07
**/
public void create(T[] vertexValues, EdgeNode<W>[][] edges, int type) {
this.type = type;
this.vertexNum = vertexValues.length;
int edgeNumTmp = 0;
for (int i = 0; i < vertexValues.length; i++) {
VertexNode<T, W> vertexNode = null;
if (null != vertexValues[i]) {
vertexNode = new VertexNode<>();
vertexNode.setVertex(vertexValues[i]);
if (null != edges && null != edges[i]) {
edgeNumTmp += edges[i].length;
// 处理第一个邻接顶点
if (edges[i].length > 0) {
EdgeNode<W> firstEdge = edges[i][0];
vertexNode.setFirstEdge(firstEdge);
}
for (int j = 1; j < edges[i].length && null != edges[i][j]; j++) {
// 处理后续邻接顶点
EdgeNode<W> edgeNode = edges[i][j];
EdgeNode<W> lastNode = edges[i][j - 1];
lastNode.setNext(edgeNode);
}
}
}
vertexes[i] = vertexNode;
}
if (type == 1 || type == 3) {
// 无向图和无向网图的边的数量，是所有单链表结点的总数的一半
this.edgeNum = edgeNumTmp / 2;
} else if (type == 2 || type == 4) {
// 有向图和有向网图的弧的数量，是所有单链表结点的总数的一半
this.edgeNum = edgeNumTmp;
}
}
类似如下调用创建一个本节中所绘的无向图：
@Test
@SuppressWarnings("unchecked")
void create() {
// 无向图
String[] vertexValues = new String[]{"D", "A", "C", "B"};
EdgeNode<Integer>[][] edges = (EdgeNode<Integer>[][]) new EdgeNode[][]{
{new EdgeNode<>(1, Integer.MAX_VALUE), new EdgeNode<>(2, Integer.MAX_VALUE)},
{new EdgeNode<>(0, Integer.MAX_VALUE), new EdgeNode<>(2, Integer.MAX_VALUE),
new EdgeNode<>(3, Integer.MAX_VALUE)},
{new EdgeNode<>(0, Integer.MAX_VALUE), new EdgeNode<>(1, Integer.MAX_VALUE),
new EdgeNode<>(3, Integer.MAX_VALUE)},
{new EdgeNode<>(1, Integer.MAX_VALUE), new EdgeNode<>(2, Integer.MAX_VALUE)}
};
graph.create(vertexValues, edges, 1);
Assertions.assertEquals(4, graph.vertexNum());
Assertions.assertEquals(5, graph.edgeNum());
}
3.3 十字链表
在使用邻接表存储有向图或有向网时，弧表要么使用邻接表，要么使用逆邻接表，邻接表能很快找到出度，但要找到入度，则必须遍历整个图才行，逆邻接表则反之。
把邻接表和逆邻接表结合起来对图进行存储的方式，被称为十字链表。
十字链表在邻接表的基础上，顶点结构由firstEdge改为firstIn和firstOut，分别表示第一个入边表中的第一个结点和第一个出边表中的第一个结点：
边或弧表结点由index和nex，变更为tailIndex、headIndex、nextTail和nextHead，分别表示弧起点在顶点表的下标、弧终点在顶点表的下标、指向下一个弧起点的指针、指向下一个弧终点的指针：
生成存储结构的过程是：
(1) 把所有的弧转变成弧结点，并让弧结点的尾巴与顶点数组对齐，若有多个弧结点的尾巴为某顶点X，则按弧的头的下标从小到大往后排；
(2) 从第一个顶点X开始，先找In列表，再找Out列表：
1) In列表，先找到所有指向顶点X的弧，例如<a1, X>、<a2, X>、<a3, X>，这三个弧的尾巴分别是a1、a2、a3，假设它们的下标分别是3、1、2，接下来，让顶点X的firstIn指向尾巴最小的那个弧，即<a2, X>，让<a2, X>的nextTail指向尾巴次小的那个弧，即<a3, X>，令<a3, X>的nextTail指向尾巴次次小的那个弧，即<a1, X>，依此类推，直到把所有指向顶点X的弧连起来；
2） Out列表，先找到所有顶点X指向的弧结点，例如<X, b1>、<X, b2>、<X,b3>，这三个弧的头分别是b1、b2、b3，假设它们的下标分别是5、4、6，然后让顶点X的firstOut指向头下标最小的那个弧结点，即<X, b2>，令<X, b2>的nextHead指向头下标次小的那个弧结点，即<X, b1>，令<X, b1>的nextHead指向头下标次次小的那个弧结点，即<X, b3>，依此类推，直到所有X指向的弧结点连接完毕；
(3) 接着按照(2)处理其他顶点，直到所有顶点处理完毕；
假设我们要构建如下有序网的十字链表结构：
首先，使用弧表结点，把所有弧画出来，所有弧的尾部（就是箭头的尾巴）与顶点数组对齐，若有多个弧结点的尾巴为某顶点X，则按弧的头的下标从小到大往后排，例如<C,A>和<C,B>，弧尾巴都是C，但A的下标小于B，因此<C,A>在前，<C,B>在后：
然后处理顶点D，找到所有指向D的弧结点，只有<A,D>，令D的firstIn指向<A,D>；然后找到所有D指向的弧结点，不存在，因此D的firstOut为空：
然后处理顶点A，找到所有指向A的弧，有<C,A>和<B,A>，C的下标小于B，因此令A的firstIn指向<C,A>，<C,A>的nextTail指向<B,A>；然后找到所有A指向的弧，只有<A,D>，因此令A的firstOut指向<A,D>：
同样的规则处理顶点C和B：
注意看，总共有10条连线，将它除以2，就是图上的箭头数量。
把图进行整理，没有连线的nextTail和nextHead标为空，得到最终结果：
十字链表的弧结点如下定义：
import lombok.Data;
/**
* 十字链表中弧表的结点
* <p>
* W表示权值类型
*
* @author Korbin
* @date 2023-01-31 16:01:11
**/
@Data
public class AcrossLinkEdgeNode<W> {
/**
* 本顶点作为尾，其头所在的顶点下标
**/
private int headIndex;
/**
* 本顶点作为尾，其头所在的下一个弧结点
**/
private AcrossLinkEdgeNode<W> nextHead;
/**
* 本顶点作为头，其尾巴所在的下一个弧结点
**/
private AcrossLinkEdgeNode<W> nextTail;
/**
* 本顶点作为头，其尾巴所在的顶点下标
**/
private int tailIndex;
/**
* 权值
**/
private W weight;
}
顶点结点如下定义：
import lombok.Data;
/**
* 十字链表中弧表的结点顶点表结点
* <p>
* T表示顶点类型
* <p>
* W表示权值类型
*
* @author Korbin
* @date 2023-01-31 16:05:38
**/
@Data
public class AcrossLinkVertexNode<T, W> {
/**
* 本结点作为尾巴，第一个弧的弧结点
**/
private AcrossLinkEdgeNode<W> firstIn;
/**
* 本结点作为头，第一个弧的弧结点
**/
private AcrossLinkEdgeNode<W> firstOut;
/**
* 顶点
**/
private T vertex;
}
构建十字链表方法如下：
/**
* 按照顶点数组、尾巴链表集和头链表集构造十字链表
* <p>
* 边的数量为单链表结点数量之和的一半
*
* @param vertexValues 顶点集
* @param firstIns firstIn数组
* @param firstOuts firstOut数组
* @param type 图类型
* @author Korbin
* @date 2023-01-31 14:23:07
**/
public void create(T[] vertexValues, AcrossLinkEdgeNode<W>[] firstIns, AcrossLinkEdgeNode<W>[] firstOuts,
int type) {
this.type = type;
this.vertexNum = vertexValues.length;
int edgeNumTmp = 0;
for (int i = 0; i < vertexValues.length; i++) {
AcrossLinkVertexNode<T, W> vertexNode = new AcrossLinkVertexNode<>();
vertexNode.setVertex(vertexValues[i]);
// 先来处理firstIn
if (null != firstIns && null != firstIns[i]) {
vertexNode.setFirstIn(firstIns[i]);
// 计算边的数量，首先是顶点与firstIn的连线
edgeNumTmp++;
// 然后看firstIn有没有nextTail，有则连线加1
AcrossLinkEdgeNode<W> node = firstIns[i].getNextTail();
while (null != node) {
edgeNumTmp++;
node = node.getNextTail();
}
}
// 再来处理firstOut
if (null != firstOuts && null != firstOuts[i]) {
vertexNode.setFirstOut(firstOuts[i]);
// 计算边的数量，首先是顶点与firstOut的连线
edgeNumTmp++;
// 然后看firstOut有没有nextHead，有则连线加1
AcrossLinkEdgeNode<W> node = firstOuts[i].getNextHead();
while (null != node) {
edgeNumTmp++;
node = node.getNextHead();
}
}
vertexes[i] = vertexNode;
}
this.edgeNum = edgeNumTmp / 2;
}
注意，边的数量是连线数量的一半。
使用类似如下方法调用创建十字链表接口：
@Test
@SuppressWarnings("unchecked")
void create() {
String[] vertexes = new String[]{"D", "A", "C", "B"};
// 创建弧结点
AcrossLinkEdgeNode<Integer> node1 = new AcrossLinkEdgeNode<>();
node1.setTailIndex(1);
node1.setHeadIndex(0);
node1.setWeight(16);
AcrossLinkEdgeNode<Integer> node2 = new AcrossLinkEdgeNode<>();
node2.setTailIndex(2);
node2.setHeadIndex(1);
node2.setWeight(17);
AcrossLinkEdgeNode<Integer> node3 = new AcrossLinkEdgeNode<>();
node3.setTailIndex(3);
node3.setHeadIndex(1);
node3.setWeight(15);
AcrossLinkEdgeNode<Integer> node4 = new AcrossLinkEdgeNode<>();
node4.setTailIndex(3);
node4.setHeadIndex(2);
node4.setWeight(0);
// 设置弧结点的关系
// 第一个弧结点没有nextTail也没有nextHead
// 第二个弧结点的nextTail是node3，没有nextHead
node2.setNextTail(node3);
// 第三个弧结点的nextTail没有，nextHead是node4
node3.setNextHead(node4);
// 第四个弧结点的nextTail没有,nextHead也没有
// 然后生成firstIns和firstOuts
AcrossLinkEdgeNode<Integer>[] firstIns = new AcrossLinkEdgeNode[]{node1,node2,node4,null};
AcrossLinkEdgeNode<Integer>[] firstOuts = new AcrossLinkEdgeNode[]{null,node1,node2,node3};
acrossLink.create(vertexes, firstIns, firstOuts, 4);
Assertions.assertEquals(4, acrossLink.vertexNum());
Assertions.assertEquals(4, acrossLink.edgeNum());
}
3.4 邻接多重表
十字链表是对有向图（网）的邻接表做的优化，这种优化对无向图（网）的邻接表存储并没有什么益处，因此无向图没有tail，也没有head。
对于无向图（网），如果需要更高效地对边进行操作时，可以使用邻接多重表对图进行存储。
依然是基于邻接表进行优化，把边表结点结构进行改造：
iVex和jVex表示顶点的下标，这个下标，是我们在定义顶点时所设定的，例如vertex[4]={D,A,C,B}，iLink指向依附于顶点iVex的下一条边，jLink指向依附于顶点jVex的下一条边。
以下列无向网为例：
我们先把每个顶点的第一条边画出来，并与顶点数组连接起来，第一条边即从顶点X开始，与vertex数组中相关的顶点的下标最小的那个顶点的连线：
然后补全其他边，补图时，令下标较小的顶点在前面，如下面的(C,B)的边：
接下来开始连线，规则是：
(1) 从第一个边结点开始，从图中找到依附iVex（假设为X）的边对应的边结点；
(2) 将iLink连接到这些边结点中，jVex等于X的结点上，若有多个边结点的jVex等于X，则取下标较小的那个，假设找到的是Y；
(3) 然后把Y的jLink连到下一个边结点上W上，把下一个边结点W的jLink连到下下一个边结点U上，直到连完所有相邻边结点；
(4) 按以上规则，继续处理第二个边结点，直到所有vertex数组中的firstEdge都处理完为止；
以上图为例，首先是边结点(D,A)，iVex为D，依附D的边对应的边结点有(D,A)和(C,D)，本结点即为(D,A)，因此直接将(D,A)的iLink连到(C,D)上，边结点(D,A)就处理完了：
来看边结点(A,C)，iVex为A，依附A的边对应的边结点有(D,A)、(A,C)和(B,A)，本结点即为(A,C)，第一个jVex等于A的边结点为(D,A)（因为D的下标为0，B的下标为3），因此将(A,C)的iLink指向(D,A)，将(D,A)的jLink指向(B,A)，此边结点就处理完成了：
边结点(C,D)的iVex是C，依附C的边对应的边结点是(C,D)、(A,C)和(C,B)，本结点即为(C,D)，第一个jVex为C的边结点是(A,C)，因此将(C,D)的iLink指向(A,C)，将(A,C)的jLink指向(C,B)：
边结点(B,A)的iVex是B，依附B的边对应的边结点是(B,A)和(C,B)，本结点是(B,A)，第一个jVex为B的边结点是(C,B)，因此将(B,A)的iLink连到(C,B)上：
此时，所有vertex数组中的结点都处理完毕，连线结点，发现连线的数量是10，边的数量是5，符合边的数量为连线数量一半的预期，我们再对图进行调整，得到最终结果：
由于无向表是无向的，因此边结点的设计并非固定的，所以可能一个无向图（网），可以画出多种邻接多重表存储结构。
邻接多重表的边结点如下定义：
import lombok.Data;
/**
* 邻接多重表中边表的结点
* <p>
* W表示权值类型
*
* @author Korbin
* @date 2023-01-31 16:01:11
**/
@Data
public class AdjacencyMultiEdgeNode<W> {
/**
* 下一个领队iVex的边结点
**/
private AdjacencyMultiEdgeNode<W> iLink;
/**
* 顶点的下标
**/
private int iVex;
/**
* 下一个领队iVex的边结点
**/
private AdjacencyMultiEdgeNode<W> jLink;
/**
* 顶点的下标
**/
private int jVex;
/**
* 权值
**/
private W weight;
}
顶点结点如下定义：
import lombok.Data;
/**
* 邻接多重表顶点表结点
* <p>
* T表示顶点类型
* <p>
* W表示权值类型
*
* @author Korbin
* @date 2023-01-31 16:05:38
**/
@Data
public class AdjacencyMultiVertexNode<T, W> {
/**
* 边表头指针，也即第一个邻接点的位置
**/
private AdjacencyMultiEdgeNode<W> firstEdge;
/**
* 顶点
**/
private T vertex;
}
构建邻接多重表的方法类似如下：
/**
* 按照顶点集值vertexValues和边或弧链表结点数组构造图
* <p>
* 边的数量是连接数的一半
*
* @param vertexValues 顶点集
* @param firstEdges firstEdge数组
* @param type 图类型
* @author Korbin
* @date 2023-01-31 14:23:07
**/
public void create(T[] vertexValues, AdjacencyMultiEdgeNode<W>[] firstEdges, int type) {
this.type = type;
this.vertexNum = vertexValues.length;
int edgeNumTmp = 0;
for (int i = 0; i < vertexValues.length; i++) {
AdjacencyMultiVertexNode<T, W> vertexNode = new AdjacencyMultiVertexNode<>();
vertexNode.setVertex(vertexValues[i]);
if (null != firstEdges && null != firstEdges[i]) {
vertexNode.setFirstEdge(firstEdges[i]);
// 计算边
AdjacencyMultiEdgeNode<W> edge = firstEdges[i];
// 从顶点连到firstEdge的边
edgeNumTmp++;
// 按iLink、vLink、iLink、vLink的顺序迭代
AdjacencyMultiEdgeNode<W> link = edge.getILink();
while (null != link) {
edgeNumTmp++;
link = link.getJLink();
}
}
vertexes[i] = vertexNode;
}
// 边数量是连接数的一半
this.edgeNum = edgeNumTmp / 2;
}
采用如下方式调用：
@Test
@SuppressWarnings("unchecked")
void create() {
String[] vertexValues = new String[]{"D","A","C","B"};
// 定义边结点
AdjacencyMultiEdgeNode<Integer> node1 = new AdjacencyMultiEdgeNode<>();
node1.setIVex(0);
node1.setJVex(1);
node1.setWeight(30);
AdjacencyMultiEdgeNode<Integer> node2 = new AdjacencyMultiEdgeNode<>();
node2.setIVex(1);
node2.setJVex(2);
node2.setWeight(20);
AdjacencyMultiEdgeNode<Integer> node3 = new AdjacencyMultiEdgeNode<>();
node3.setIVex(2);
node3.setJVex(0);
node3.setWeight(40);
AdjacencyMultiEdgeNode<Integer> node4 = new AdjacencyMultiEdgeNode<>();
node4.setIVex(3);
node4.setJVex(1);
node4.setWeight(10);
AdjacencyMultiEdgeNode<Integer> node5 = new AdjacencyMultiEdgeNode<>();
node5.setIVex(2);
node5.setJVex(3);
node5.setWeight(0);
// 设置边结点关系
node1.setILink(node3);
node1.setJLink(node4);
node2.setILink(node1);
node2.setJLink(node5);
node3.setILink(node2);
node4.setILink(node5);
AdjacencyMultiEdgeNode<Integer>[] firstEdges = new AdjacencyMultiEdgeNode[]{node1, node2, node3, node4};
graph.create(vertexValues,firstEdges,3);
Assertions.assertEquals(4, graph.vertexNum());
Assertions.assertEquals(5, graph.edgeNum());
}
3.5 边集数组
边集数组是由两个一维数组构成，一个是存储顶点的信息，另一个是存储边的信息，这个边数组每个元素由一条边的起点下标（begin）、终点下标（end）和权（weight）组成，注意，对于无向图（网），可以选择任何一个边的顶点作为起始和终点。
显然边集数组关注的是边的集合，在边集数组中要查找一个顶点的度需要扫描整个边数组，效率并不高。因此它更适合对边依次进行处理的操作，而不适合对顶点相关的操作。
边集数组的结构会比较简单：
边集表的边或弧结点定义如下：
import lombok.Data;
/**
* 边集表的边结点
*
* @author Korbin
* @date 2023-02-02 14:49:24
**/
@Data
public class EdgeListEdgeNode<W> {
/**
* 边或弧的起点
**/
private int begin;
/**
* 边或弧的终点
**/
private int end;
/**
* 权值
**/
private W weight;
/**
* 构造子
**/
public EdgeListEdgeNode(int begin, int end, W weight) {
this.begin = begin;
this.end = end;
this.weight = weight;
}
}
构造代码很简单，基本不需要做什么特殊处理：
/**
* 按照顶点集vertex和边或弧结点数组arc定义构建图
*
* @param vertex 顶点集
* @param arc 边或弧结点数组
* @param type 图类型
* @author Korbin
* @date 2023-01-31 14:23:07
**/
public void create(T[] vertex, EdgeListEdgeNode<W>[] arc, int type) {
this.vertex = vertex;
this.arc = arc;
this.vertexNum = vertex.length;
this.type = type;
this.edgeNum = arc.length;
}
注：本文为程 杰老师《大话数据结构》的读书笔记，其中一些示例和代码是笔者阅读后自行编制的。
2650
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
