随手记下所学知识,很多图表来自原书,仅供学习使用!
2.1 经验误差与过拟合
通常,我们使用"错误率"来表示分类中错误的样本占总样本的比例.如果m个样本中有a个错误样本则错误率E=a/m
,对应的,1-a/m称为精度,即"精度"=1-"错误率".更一般的情况来说,我们把机器学习的预测输出和样本真实输出之间的差异称为"训练误差"或者"经验误差".
一般来说,如果在训练集中的表现精度高,而在测试集中表现的精度小,一般是过拟合.相反,如果是精度都不高一般是欠拟合.我们本来的目的是把训练集这一类的特征学出来,也就是要找训练集和测试集的共同特征,但是,虽然类有共性,但是每个个体之间是有差异的,如果是把训练集自身的特征当成了这一类的特征,就是过拟合,如果,没有学到什么,训练集(有可能训练集也不低)测试集精度低,一般就是过拟合.比如说,训练的时候是用的哈士奇,但是测试的时候是金毛,如果因为金毛耳朵,颜色和哈士奇不一样而不认为金毛是狗,就是过拟合,但是如果是因为看到体型差不多,就认为是狗,就是欠拟合.(金毛和哈士奇图片来自网络,侵权就删...)

更加恰当的例子应该还是来自与原书.

2.2 评估方法
在测试过程中,我们一般会找一个测试集,测试集数据不在训练中出现.至于为怎么,很容易理解,就像学生考试一样,用平时的训练题作为考试题,这样就不能考出来举一反三的能力,可以看为是机械记忆.机器学习,本来就是要做一个能够举一反三的模型,要是考记忆能力,还不如直接弄个记事本,然后Ctrl+F直接查找文件中的关键字.
那么还有一个问题,数据集就有一个,既要测试,又要训练应该如何做呢?很简单,分一为二.直接把一个数据集分成两个,一个作为数据集,一个作为训练集.
2.2.1留出法
"留出法"是将数据集分成两个相斥的集合.但是要保证是均匀的划分,简单的说是把数据集打乱以后在里面抽取多少是个有效的办法.例如,对于判断是否是树叶这个数据中,把是的一类和不是的分开.那么这个划分基本上就是没有意义的.
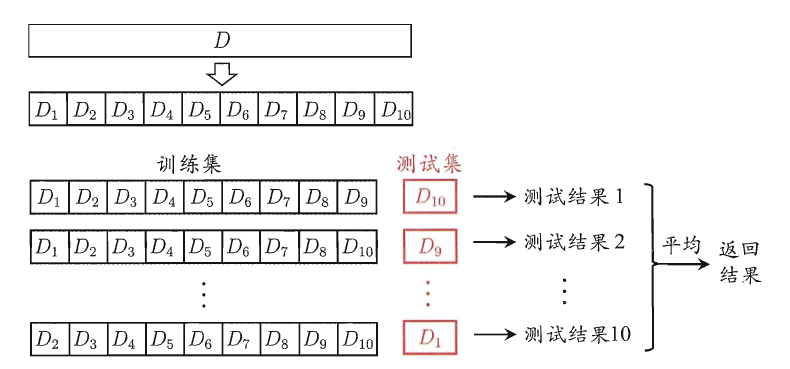
2.2.2 交叉验证法
其实上面的划分方法有个问题,就是貌似没有充分利用每个数据来训练模型.对于这个问题,人们又想到了一个方法,就是把数据混合均匀以后,分成没有交集的k份,每一次把其中的一份作为测试,其他作为训练,然后对k个结果求平均.这个方法成为"K折交叉验证",一般人们把k取值为10.如果有m的数据而k=m,那么这个情况就比较特殊了,就被成为了"留一法".留一法能够保证让每次的训练集和原来的数据集尽可能的接近,从而保证了准确性.但是,想想就知道,恐怕要训练测试m次了,而m很大的时候,几乎不可能实现(当然,有恒心有毅力者大有人在).
简单的图片来说明就是:
2.2.3 自助法
自助法,就是一个高中概率常见的模型,有放回的摸小球的问题.就是把数据集混合均匀以后,开始有放回的抽取m次,作为训练集,然后把数据集和训练集的差集作为测试集.
在概率中解释这个情况就是,
也就是有0.368的数据在测试集.好熟悉的公式,考研数学没白看...
2.2.4 调参数与最终模型
有人说,机器学习尤其是神经网络,就是调参。这个我也不知道是不是对的,但是调参是很重要的,据说厉害的人知道每一个参数与结果的关系,不断调整然后结果自然就好了,而盲目调参,就是碰运气咯。这个肯定是根据后面的章节的知识进行操作的。
2.3 性能度量
性能度量,顾名思义就是考察对比不同算法的好坏的,衡量模型泛化能力的评价标准,就是性能度量。
懒得写了,贴点原书的“均方误差”。
但是还有的性能度量:
2.3.1 错误率与精度
错误率与精度的公式为:
在这里,我感觉就是宏观来看,数据集的平均错误率和准确率,就是拿一个数据出来错误的概率和正确的概率。
而当加入了一个概率密度,就成了概率的概率了.
2.3.2 查准率、查全率和F1
首先看看二分问题的结果混肴矩阵来看查准率和查全率:
查准率P简单的说就是所有正例中正确的概率,而查全率R就是判断为正例中有多少是对了的。既然有了查准率和查全率两个参数,似乎就能够搞点事情了。
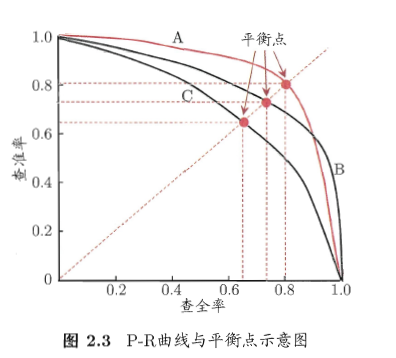
下图就是一个2D的表格,有了两个值P和R了嘛。
这样,就有了P-R图,对图中于 A,B,C三个模型哪个更好呢?评价又是一个问题。但是我们发现,PR双高的,就是一个凸的曲线,这样比较面积就OK了。但是又面临的一个问题是面积不好弄啊,既要测出来模型的曲线还要积分面积。那么有没有更好的办法呢?答案是肯定的,就是图中的平衡点,就是P=R的时候的取值。
但是,大家又嫌弃平衡点(BEP)简单粗暴,于是搞了个F1度量:
然后这个公式有个特点是P、R权重是一样的,然后加权重以后就是:
如果说为啥R上面没加什么东西,那么实际上这个β已经相当于加了,效果一样。因为从根本上讲削弱一个就是加强另一个,多一个参数不如少一个参数啊!
再将这一套扩展到多个二分类混肴矩阵,看他们的宏观情况,这个公司就进行了拓展:
请不要忘了,从根本上看,其实还是那一套。。。
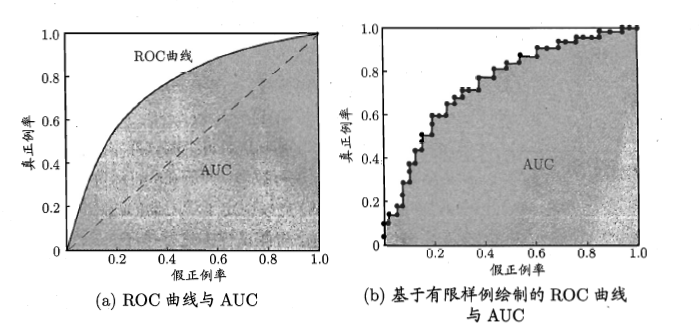
2.3.3 ROC与AUC
ROC全称是“受试者工作特征”。其实就是上面的p-r图的坐标换了换。
这个判断标准和P-R图一样,看面积。当看到b图的时候,是不是想起了积分了呢?
这里注意的是那个数学符号。。。指示符号,条件成立为 1 否则为 0,这里也要好好想想。
2.3.4 代价敏感错误率与代价曲线
嗯,生活中,有大错误也有小错误。大错误一旦犯了,就麻烦了,小错误可能天天犯都没事啊。所以,这里引入了代价问题,看看错误是致命错误还是小毛病。
在这里 cost01和cost10 可以不一样,这样,犯了不同错误会受到不同惩罚。
嗯,还是对基本公式的一个改造。
2.4 比较检验
2.4.1 假设检验
看到这一节开始,我感觉我学的是假计算机,感觉好像进入了数学系。。。
貌似本小结开始前,应该先想想那个排列组合,比如说,有m个小球,不放回的抽取e个小球标记为错误,其他的标记为正确,那么有几种可能?这样想一下,原书中的公式似乎就熟悉多了呢。
这样实际上就是一个二项分布(二项分布即重复n次独立的伯努利试验。在每次试验中只有两种可能的结果,而且两种结果发生与否互相对立,并且相互独立,与其它各次试验结果无关,事件发生与否的概率在每一次独立试验中都保持不变,则这一系列试验总称为n重伯努利实验,当试验次数为1时,二项分布服从0-1分布。)。
发现还得看看概率论与数理统计才是比较靠谱的。
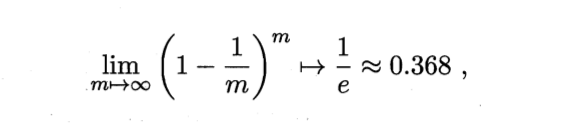








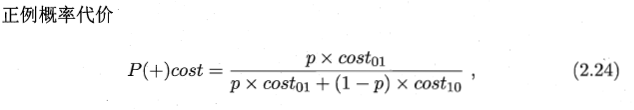

























 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








