CNDO-INTGRL-SS-BINTGS-斯莱特轨道指数--- 精确方法

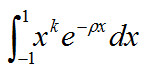
因为上一节得到的递推方法有精度误差，因此需要得到计算这个积分的精确的方法，

Approximate Molecular Orbital Theory by Pople John A., Beveridge David L.p182

由python

print (  (sympy.integrate(  x**k*exp(-p*x)  ,( x, -1 , 1   ) ) )  )得到

-k*p**(-k)*gamma(k + 1)*lowergamma(k + 1, -p)/(p*gamma(k + 2)) + k*p**(-k)*gamma(k + 1)*lowergamma(k + 1, p)/(p*gamma(k + 2)) - p**(-k)*gamma(k + 1)*lowergamma(k + 1, -p)/(p*gamma(k + 2)) + p**(-k)*gamma(k + 1)*lowergamma(k + 1, p)/(p*gamma(k + 2))

经化简

 

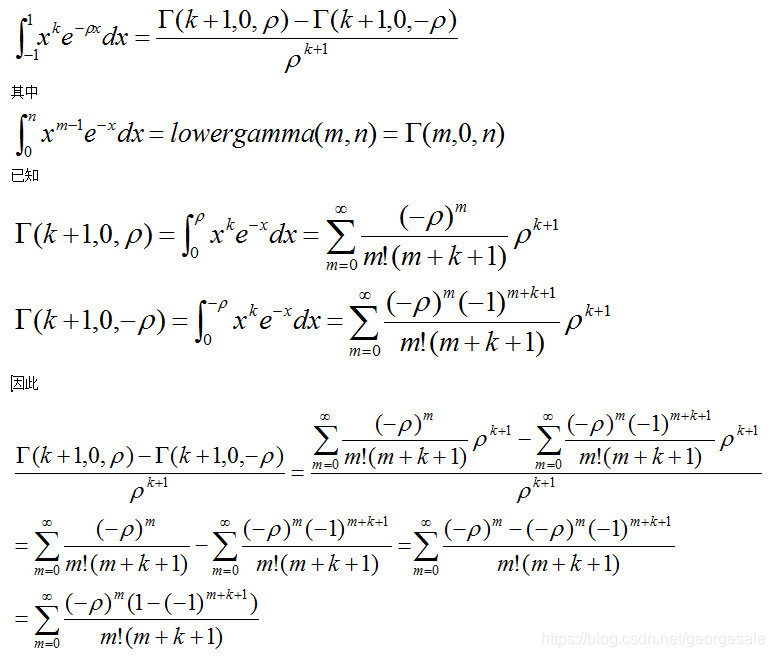
所以对应的程序是

public static  void BINTGS140( double ρ, int i0,int k,int last, double []b   ) throws IOException, ParseException {
				for(int i=i0;i<k+1;i++) {
					double yt=0.0;
					
					for(int m=i0 ;m<last+1 ;m++) {
						
	    yt=yt+Math.pow((-ρ),m )*(1-  Math.pow((-1) , (m+i+1) )    )  /( FACT(m)*(double)(m+i+1));
			 b[i]=yt;
					 
			
					}
						
				}
				
			}

验算

double []b=new double[17];

BINTGS140(  0.6 , 0 ,13 ,17 , b   ) = -0.08430403604574815

wolframalpha

Integrate[ x**13*exp(-0.6*x),{x,-1,1}]=-0.084304036045748143556492453678859949065231785751955121973510012...