模拟退火算法有4个参数
N:每个温度迭代次数
T:重复降温次数
a:降温系数
t0:初始温度
本文用一个50个城市的TSP问题数据集,用交叉对比的方法调参。一组参数运行200次取平均。
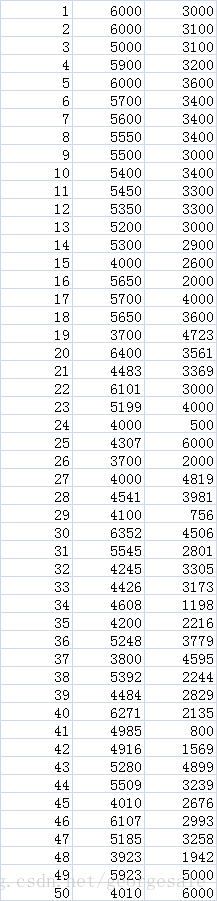
首先调初始温度
N=1000,T=1000,a=0.99固定


可以看到在初始温度在1500时平均距离和标准差就几乎没有什么变化了。也就是初始温度在大于1500以后对结果已经没有什么影响。产生这种效果的原因是
模拟退火算法最重要的判断条件
Math.exp(差值/t)>r(0-1的随机数)
因为0-1之间随机平均下来就是0.5
Math.exp(-0.69)=0.5
也就是说-0.69< 差值/t <0 时Math.exp(差值/t)>0.5
所以大致可以将模拟退火算法理解成只要 差值的绝对值在t的0.7倍以内就会被采用。因为温度t随着迭代逐渐降低,t*0.7显然逐渐变得更小,实现了退火。
所以t0*a^N这个值对退火算法最为重要。
比如 1500*0.99^1000=0.06,0.06*0.7这个冗余度对计算路径太小了已经没什么意义。
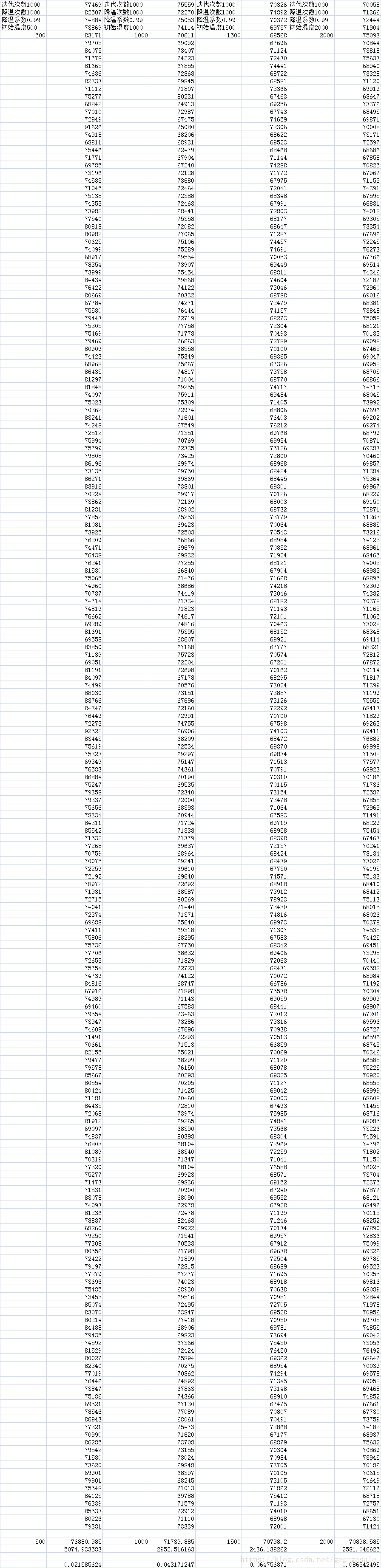
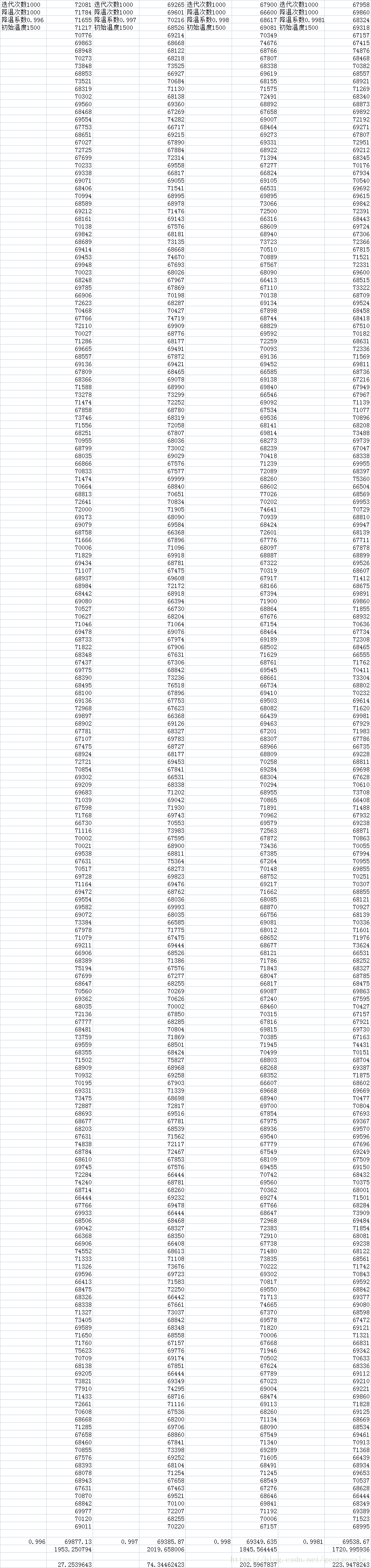
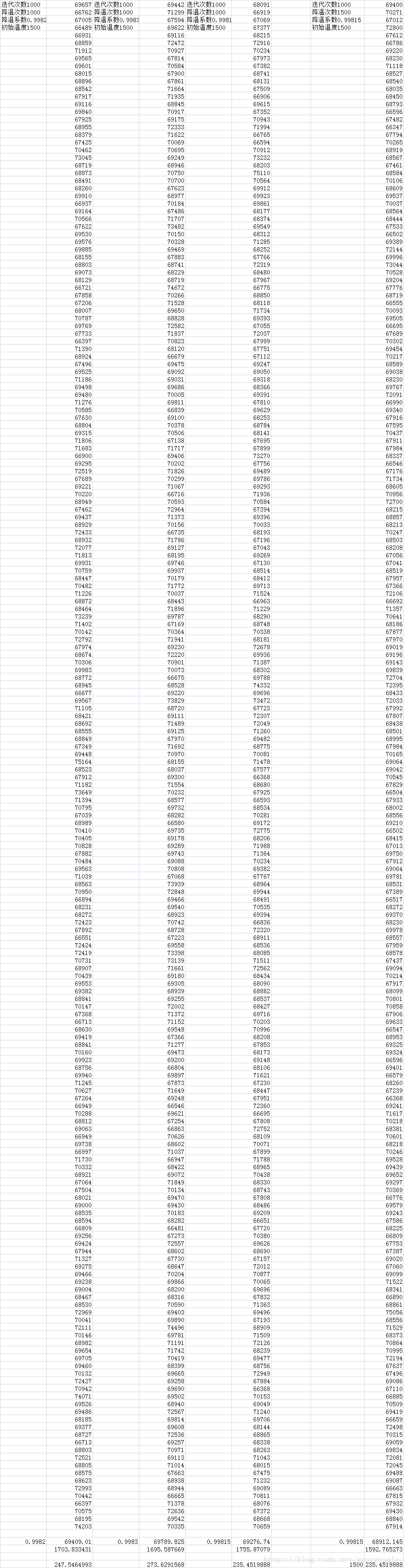
第二步,调节降温系数
N=1000,T=1000,t0=1500固定


当降温系数=0.99815时平均距离为69276最优,这时t0*a^N=235,这道题的最短路径可能在66221附近,235*0.7/66221=0.002,这个冗余度相当于最优值的0.2%。
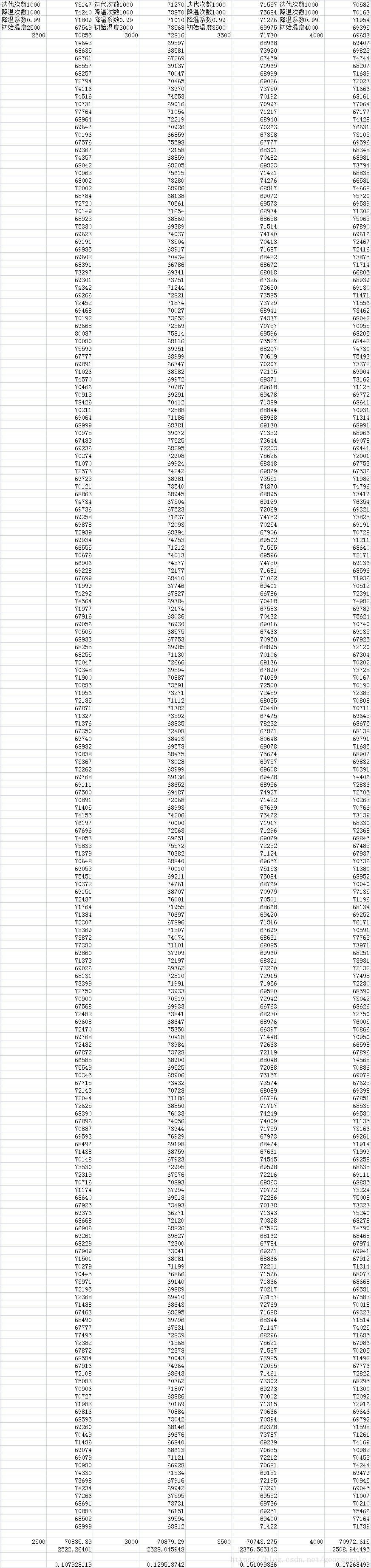
第三步调重复降温次数T
N=1000,a=0.99815,t0=1500固定

这组结果很明显同一个过程重复次数越多性能越好。但T越大速度也越慢,所以T取2500.因为每个温度迭代次数=1000固定所以t0*a^N也都是固定的。
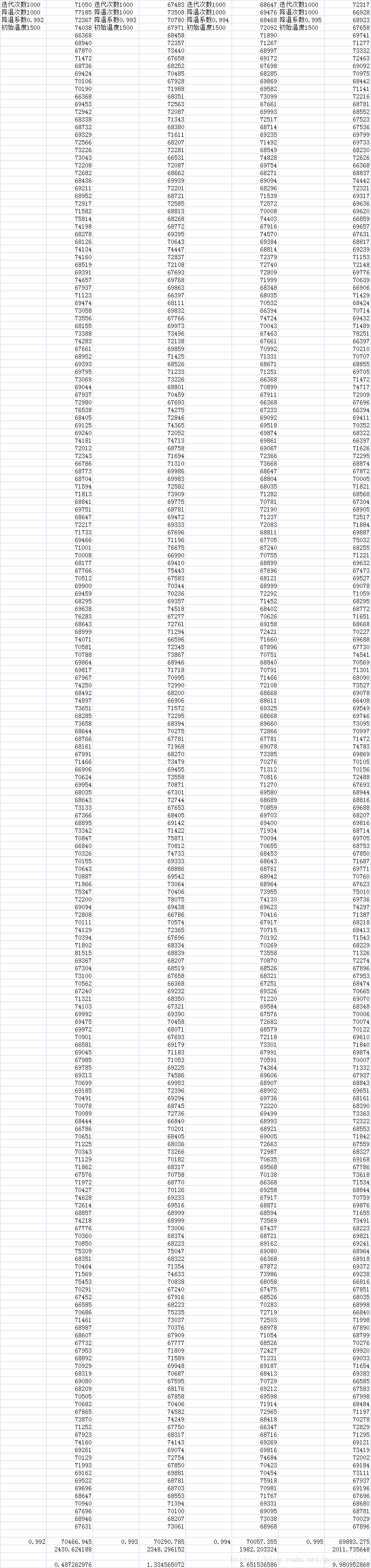
第四步调节每个温度迭代次数N
T=2500,a=0.99815,t0=1500固定

这个很明显随着N的变化t0*a^N也显著变化,结果变差。
所以综合起来退火算法的四个参数
N:每个温度迭代次数
T:重复降温次数
a:降温系数
t0:初始温度
T越大性能越优,
N,a,t0这个三个变量是相互制约的,t0*a^N的值是退火算法最为关键的因素。一个大致可以参考的标准是t0*a^N*0.7/理论最优值=0.002。
这个测试和蚁群算法的测试用的数据集是一样的
虽然退火算法的最好平均值大于蚁群算法,
但是模拟退火算法的最优值是66221,这个最优值好于蚁群算法, 而且这个最优值多次出现,表明退火算法更有利于搜索全局最优值。





























 544
544

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










