用分离变量法把波函数
![]()
分离成径向部分和角度部分
![]()
径向函数Rnl为

球谐函数Ylm为

由此计算氢原子n=1,2,3时的能级
其中z是核电荷数代入1.a0是波尔半径,用原子单位表示代入1,
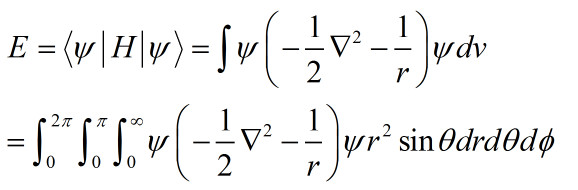
拉普拉斯算符为
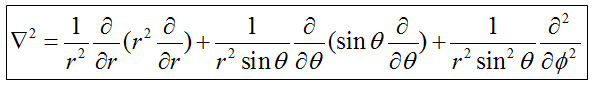
代入Ψ可得到

动能和势能比为-1/2符合维里定理。
Ψ3,2,0的python代码为
import sympy
import math
from sympy import symbols, cancel
a = sympy.Symbol('a')
e = sympy.Symbol('e')
m = sympy.Symbol('m')
h = sympy.Symbol('h')
l = sympy.Symbol('l')
r = sympy.Symbol('r')
EE = sympy.Symbol('EE')
x = sympy.Symbol('x')
y = sympy.Symbol('y')
z = sympy.Symbol('z')
θ= sympy.Symbol('θ')
Ψ= sympy.Symbol('Ψ')
Φ= sympy.Symbol('Φ')
pi=sympy.Symbol('pi')
E=sympy.Symbol('E')
I=sympy.Symbol('I')
sin=sympy.Symbol('sin')
cos=sympy.Symbol('cos')
diff=sympy.Symbol('diff')
integrate=sympy.Symbol(' integrate')
pi=sympy.pi
E=sympy.E
sin=sympy.sin
cos=sympy.cos
diff=sympy.diff
integrate=sympy.integrate
fx=(2)**(1.5)* 1/(81*15**0.5) *r**2*sympy.exp(-r/3)* ( 5/(16*pi))**0.5*(3*cos(θ)*cos(θ) -1)
f1=( 1/(r*r) ) *diff ( ( r*r*diff(fx,r)) ,r)
f2=( 1/(r*r*sin(θ)) ) * diff( ( sin(θ)*diff(fx,θ) ) ,θ)
f3=( 1/(r*r*sin(θ)*sin(θ) ) )* diff(fx,Φ,Φ)
f8=(-1/2)*(f1+f2+f3)*fx
#print ( f1 )
#print ( f2 )
#print ( f3 )
print ( f8 )
#球坐标积分
f9=( integrate( ( integrate( integrate( f8*r*r*sin(θ) , (r ,0 , float('inf') ) ) , (θ, 0 , pi ) ) ) , (Φ,0,2*pi) ) )
print ( f9 )
f10=fx*(-1/r)*fx
f11=( integrate( ( integrate( integrate( f10*r*r*sin(θ) , (r ,0 , float('inf') ) ) , (θ, 0 , pi ) ) ) , (Φ,0,2*pi) ) )
print ( f11 )
print ( f9+f11 )


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










