一个卷曲的力场

( A, B )---4*30*2---( 1, 0 )( 0, 1 )

做一个网络分类A和B，让输入只有4个节点，每个训练集里有两张图片。让B的训练集全为0，排列组合A，收敛误差为7e-4，每个收敛误差收敛199次，观察迭代次数平均值的变化。共完成了256组，但只有21组不同的迭代次数。

 

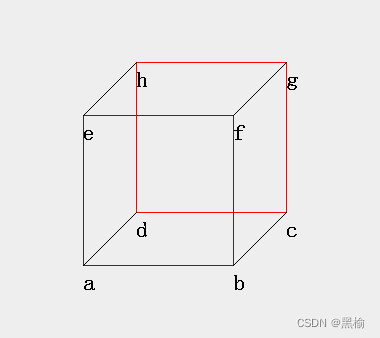
这次继续用质心高度的办法拟合这组迭代次数，将差值结构的8个点，对应为内接于球的立方体上下两个面的8条边，

设立方体边长为1，这8条边的质心为

ab	0.5	0	0
bc	1	0.5	0
cd	0.5	1	0
da	0	0.5	0
ef	0.5	0	1
fg	1	0.5	1
gh	0.5	1	1
he	0	0.5	1

差值结构				A-B	迭代次数	质心h
1	0	0	0	8*15-0*0	5609.653	0.5497722
1	1	1	1	8*15-0*0	5609.653

如计算网络8*15-0*0的质心，A中的两张图片是二进制的8和15.B的两张图片都是0.差值结构的第一行的4个点对应ab,bc,cd,da这4条边，第二行的点对应ef

质心高=半径-质心到球心的距离

ab	0.5	0	0			1	0	0	0
bc	1	0.5	0			1	1	1	1
cd	0.5	1	0
da	0	0.5	0
ef	0.5	0	1
fg	1	0.5	1
gh	0.5	1	1
he	0	0.5	1
	坐标				质量				坐标*质量
ab	0.5	0	0		1	1	1		0.5	0	0		0.5498
bc	1	0.5	0		1	1	1		1	0.5	0
cd	0.5	1	0		1	1	1		0.5	1	0
da	0	0.5	0		1	1	1		0	0.5	0
ef	0.5	0	1		1	1	1		0.5	0	1
fg	0	0	0		1	1	1		0	0	0
gh	0	0	0		1	1	1		0	0	0
he	0	0	0		1	1	1		0	0	0
							5		2.5	2	1
													圆心
									0.5	0.4	0.2		0.5	0.5	0.5
													0.5	0.4	0.2
													0	0.01	0.09
													距离
													0.3162
													0.5498

则得到质心高为0.5498.用此方法计算其他各组数据得到

差值结构				A-B	迭代次数	质心h
1	0	0	0	8*15-0*0	5609.653	0.5497722
1	1	1	1	8*15-0*0	5609.653
ab	bc	cd	da	ef
1	0	0	0	8*14-0*0	7108.93	0.5598138
1	1	1	0	8*14-0*0	7108.93
ab	bc	cd		ef
1	0	1	0	10*15-0*0	9954.879	0.699
1	1	1	1	10*15-0*0	9954.879
ab	bc	cd	da	ef	gh
0	1	0	0	4*6-0*0	10406.96	0.4577517
0	1	1	0	4*6-0*0	10406.96
ab	bc	ef
1	1	0	0	12*14-0*0	13400.23	0.621051
1	1	1	0	12*14-0*0	13400.23
ab	bc	cd	ef	fg
1	1	1	0	14*15-0*0	14575.28	0.7649847
1	1	1	1	14*15-0*0	14575.28
ab	bc	cd	da	ef	fg	gh
0	1	0	0	4*11-0*0	17557.99	0.616
1	0	1	1	4*11-0*0	17557.99
ab		cd	da		fg
0	1	0	1	5*11-0*0	17735.06	0.7245786
1	0	1	1	5*11-0*0	17735.06
ab		cd	da		fg		eh
1	1	1	1	15*15-0*0	19478.93	0.866
1	1	1	1	15*15-0*0	19478.93
ab	bc	cd	da	ef	fg	gh	he
0	1	1	1	7*7-0*0	20644.38	0.6993333
0	1	1	1	7*7-0*0	20644.38
	bc	cd	da		fg	gh	he
1	1	1	0	14*7-0*0	21404.21	0.7481489
0	1	1	1	14*7-0*0	21404.21
	bc	cd	da	ef	fg	gh
1	0	0	0	8*5-0*0	22417.49	0.6302977
0	1	0	1	8*5-0*0	22417.49
	bc		da	ef
1	0	0	1	9*9-0*0	22586.9	0.5124466
1	0	0	1	9*9-0*0	22586.9
ab	bc			ef	fg
0	1	1	0	6*12-0*0	24266.91	0.616
1	1	0	0	6*12-0*0	24266.91
ab	bc				fg	gh
1	1	1	1	15*0-0*0	27143.41	0.366
0	0	0	0	15*0-0*0	27143.41
ab	bc	cd	da
1	0	0	0	8*8-0*0	27271.99	0.366
1	0	0	0	8*8-0*0	27271.99
ab	ef
1	0	1	0	10*5-0*0	27292.43	0.866
0	1	0	1	10*5-0*0	27292.43
	bc		da	ef		gh
1	1	0	1	13*0-0*0	29277.74	0.3389537
0	0	0	0	13*0-0*0	29277.74
ab	bc	cd
1	0	0	1	9*0-0*0	33141.22	0.2536276
0	0	0	0	9*0-0*0	33141.22
ab	bc
1	0	0	0	8*4-0*0	33841.04	0.5124466
0	1	0	0	8*4-0*0	33841.04
ab	fg
0	0	0	0	0*1-0*0	41000.53	0.1588932
0	0	0	1	0*1-0*0	41000.53
ab

其中有6组8*4-0*0，10*5-0*0，6*12-0*0，14*7-0*0，5*11-0*0，4*11-0*0的数据不对，若先不考虑这6组，则得到比15*15-0*0大的对称部分迭代次数和质心的高成反比，比15*15-0*0小的非对称部分迭代次数与质心的高成正比。

人为的将这个差值结构卷成立方体可能很刻意，因为似乎有很多种卷法。但这件事也可以理解为这个差值结构仅具有数值之间相对的位置关系，没有任何特征的外部三维结构，但0*0事实上形成了一个卷曲的指向中心的引力场，差值结构在这个卷曲的力场中被扭曲成三维结构而产生了质心。