机器学习中的线性代数

第二章 线性代数

一些比较重要的概念
1.张量
类似于矢量是标量的推广，矩阵是矢量的推广一样，“张量”其实就是提供了一种描述具有任意数量轴的n为数组的通用方法。向量其实就是一阶张量，而矩阵就是二阶张量。张量用特殊的大写字符表示（例如，X、Y、Z），张量的索引机制和矩阵类似，形如：[X]i,j,k

在深度学习中，张量将变得十分重要，比如图像、声音等都不可能只用一维、二维来表示，肯定是涉及到三维及三维以上，比如图像将以n维数组形式出现，其中有3维分别对应与宽度、高度以及一个通道轴，用于表示颜色通道。

2.生成子空间
我们将每个矩阵的列向量看做是从原点出发的不同的方向，矩阵A乘以列向量b的结果，就是沿着A的列向量所代表的方向走对应的bi的距离，最后所到达的点就是结果向量，一组向量的生成子空间，就是原始向量线性组合后所能抵达的所有的点的集合。那么我们就可以将线性方程组是否有解这样理解，以Ax=b为例，要确定Ax=b是否有解，我们就可以理解为向量b是否在A的列向量的生成子空间中，即确定是否存在一个向量x,使得从原点出发沿着A所对应的列向量所代表的方向走，最后能否抵达向量b所确定的位置。

3.范数
Frobenius范数，用来衡量矩阵的大小，定义为矩阵A的各项元素的绝对值的平方求和再开方，表示为

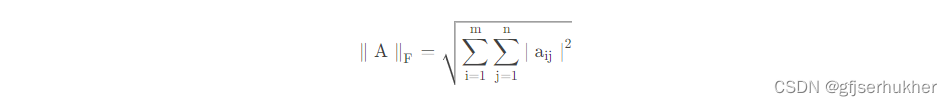
迹运算返回的是矩阵对角元素的和，因此迹运算提供了另外一种描述Frobenius范数的方式

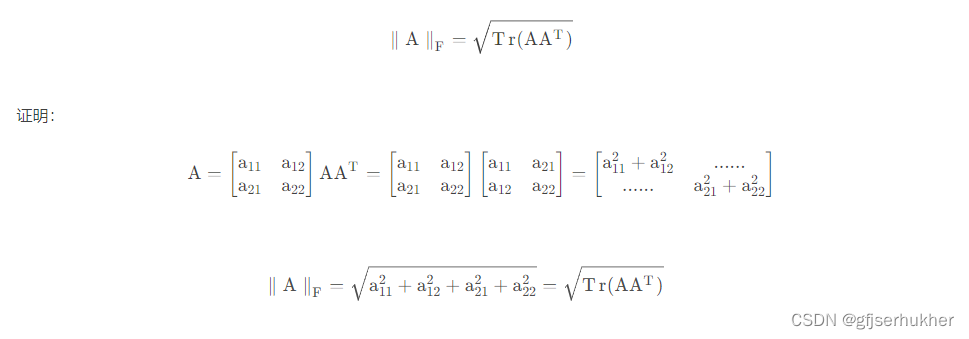
3.特征分解
所有的特征值都是正数的矩阵称为正定，所有特征值都是非负数的矩阵称为半正定矩阵。
同理，所有的特征值都是负数的矩阵称为负定矩阵，所有的特征值都是非正数的矩阵称为半负定矩阵。

4.奇异值分解
奇异值分解不像特征分解一样，对矩阵有特殊的限制，（比如要求实对称矩阵才能进行进行特征分解），奇异值分解对所有的矩阵都适用，包括非方阵；相当于更加具有一定的普适性，对矩阵A进行奇异值分解A=UDV（T），其中，U的列向量是称为A的左奇异向量，矩阵中的列向量是AA（T）的特征向量所构成，V的列向量称为A的右奇异向量，列向量是由A（T）A的特征向量所构成，而D是一个对角矩阵，其对角线上的元素就称为A的奇异值，而非零奇异值是A（T）A的特征值的平方根。

5.迹运算
多个矩阵相乘得到的方阵的迹，和将这些矩阵中的最后一个挪到最前面之后相乘的迹是相同的。当然，我们需要考虑挪动之后矩阵乘积依然定义良好：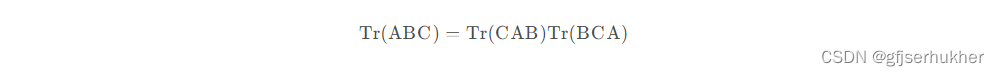
即使循环置换后矩阵乘积得到的矩阵形状变了，迹运算的结果依然不变。
除此之外，标量在迹运算后仍然是它自己：a = Tr ( a )

6.行列式
行列式的绝对值可以用来衡量矩阵参与矩阵乘法后空间扩大或者缩小了多少，如果行列式是0，那么空间至少沿着某一维完全收缩了，使其失去了原有的体积，如果行列式是1，那么这个转换保持原有空间体积不变。

7.实例（主成分分析PCA）
原理：