计算机图形学中的曲线问题——拉格朗日插值曲线绘制实践

拉格朗日插值曲线的绘制

限于篇幅，我们将在这篇文章中介绍拉格朗日插值曲线绘制实践，主文章链接：

GGN_2015
计算机图形学中的曲线问题

在主文章中我们已经介绍了拉格朗日插值函数的绘制方法。给定一个函数必须通过的点的集合，保证任意两点 $x$ 指不同，我们就能构造出一条拉格朗日插值函数。但是函数图象作为一种特殊的曲线，有着很多的我们不想要的约束，例如：

1. 函数曲线上每个 $x$ 至多只有一个 $y$ 与之对应；
2. 函数难以描述斜率不存在的位置；

因此，假如我们先要描述一条在平面甚至空间中任意“蜿蜒”的曲线，我们需要使用参数方程的方式。我们可以把平面上的参数方程理解成一个从 $\mathbb{R}$ 映射到 ${\mathbb{R}}^2$ 的映射，每一个自变量 $t$ 对应着参数方程中的一个点对 $(X_t,Y_t)$。

拉格朗日插值曲线的表示

假设我们希望我们的曲线能够依次通过 $P_1(x_1,y_1),P_2(x_2,y_2),\cdots ,P_n(x_n,y_n)$，那么我们不妨定义一个这样的参数方程：
$$M(t)=P_1\cdot f_1(t)+P_2\cdot f_2(t)\cdots +P_n\cdot f_n(t),t\in [1,n]\text{\hspace{1em}(1)}$$

其中 $f_i$ 的是一个在 $x=i$ 处取值为 $1$，在 x ∈ { 1 , 2 , ⋯   , n } 且 x ≠ i x\in\{1, 2, \cdots, n\} 且 x\neq i x∈{1,2,⋯,n}且x​=i 时 $f_i(x)=0$，这种函数的构造方法在主文章中介绍过，在此不再赘述。$(1)$ 式中，我们将 $P_i$ 与 $f_i(t)$ 依次对应相乘，这里的点 ‘$\cdot$’ 表示数乘向量，其中 $P_i$ 是二维空间的点坐标，也就是一个二维向量，$f_i(t)\in \mathbb{R}$ 是一个实数。最终我们得到的 $M(t)\in {\mathbb{R}}^2$ 是一个二维向量，我们把它视为平面中的一个动点，这个动点的轨迹就是我们的插值曲线。

根据我们之前对一般的拉格朗日插值函数的介绍，我们可以得知：
$$\begin{gathered} M(1)=P_1\cdot 1+P_2\cdot 0\cdots +P_n\cdot 0=P_1 \\ M(2)=P_1\cdot 0+P_2\cdot 1\cdots +P_n\cdot 0=P_2 \\ ⋮ \\ M(n)=P_1\cdot 0+P_2\cdot 0\cdots +P_n\cdot 1=P_n \end{gathered}$$

换言之，当 $t$ 从 $1$ 变化到 $n$ 的过程中参数方程曲线 $M(t)$ 能够依次通过 $P_1,P_2,\cdots ,P_n$ 中的每一个点。下面给出了一个包含五个结点的拉格朗日插值函数的示例：

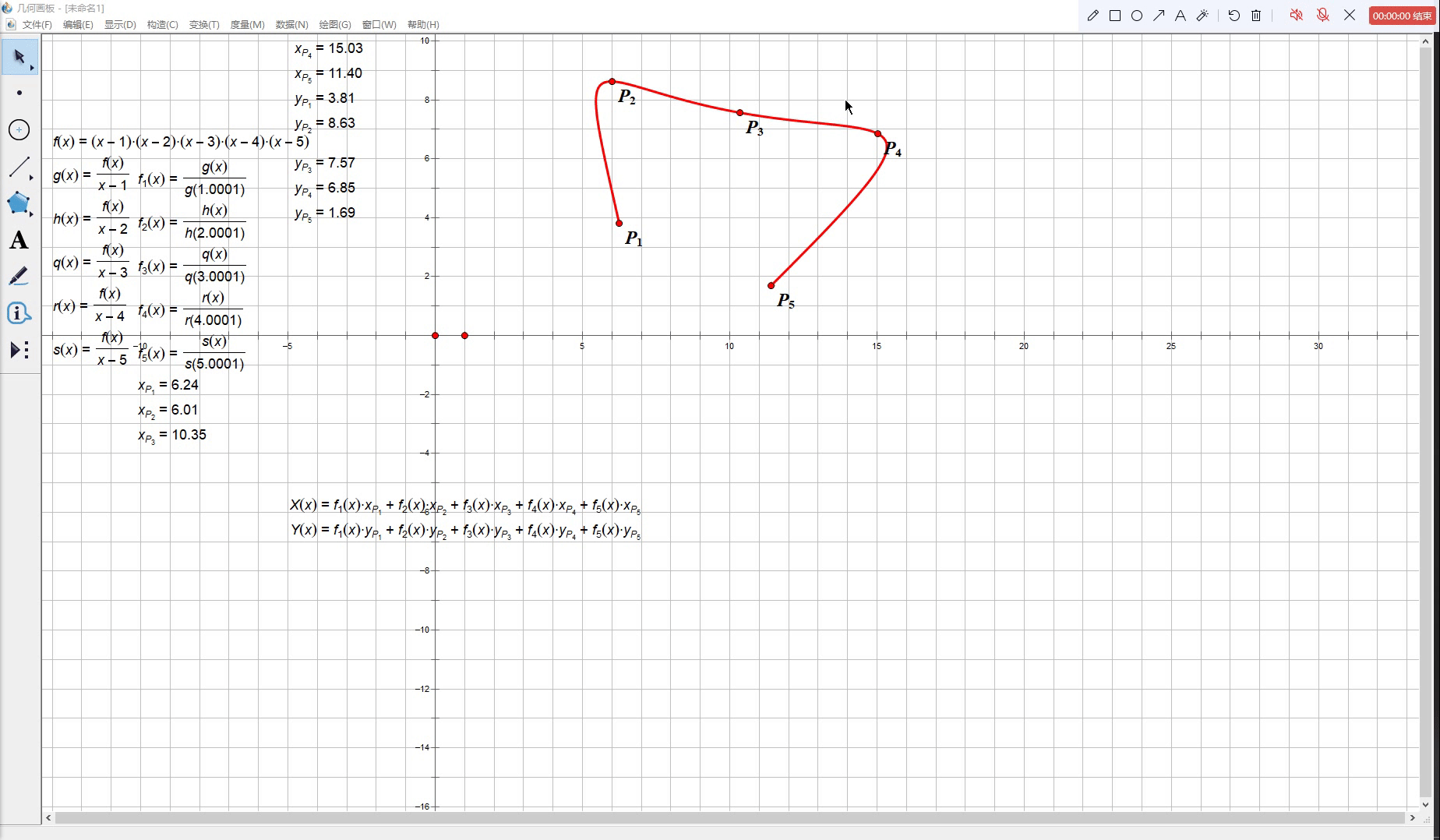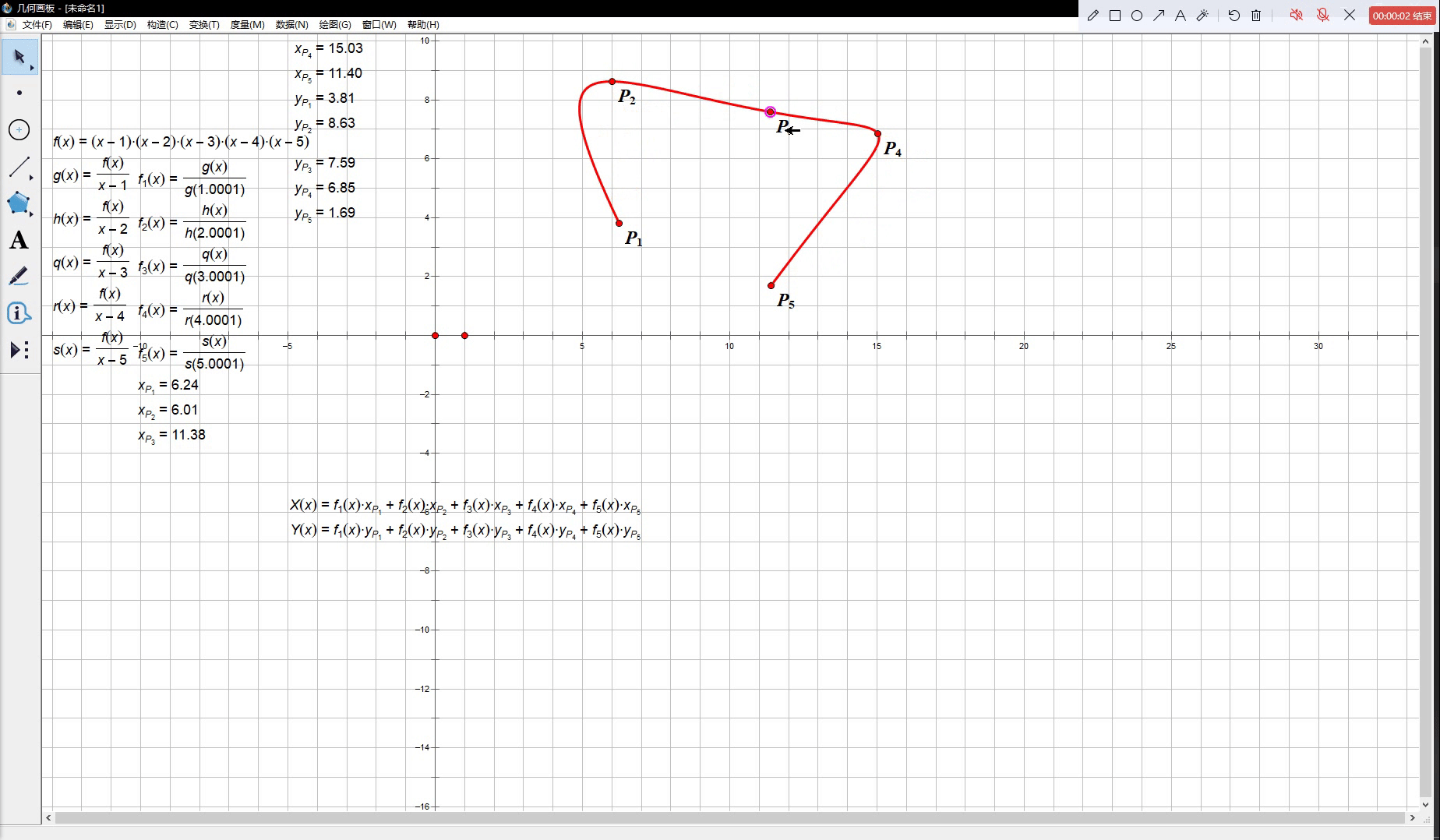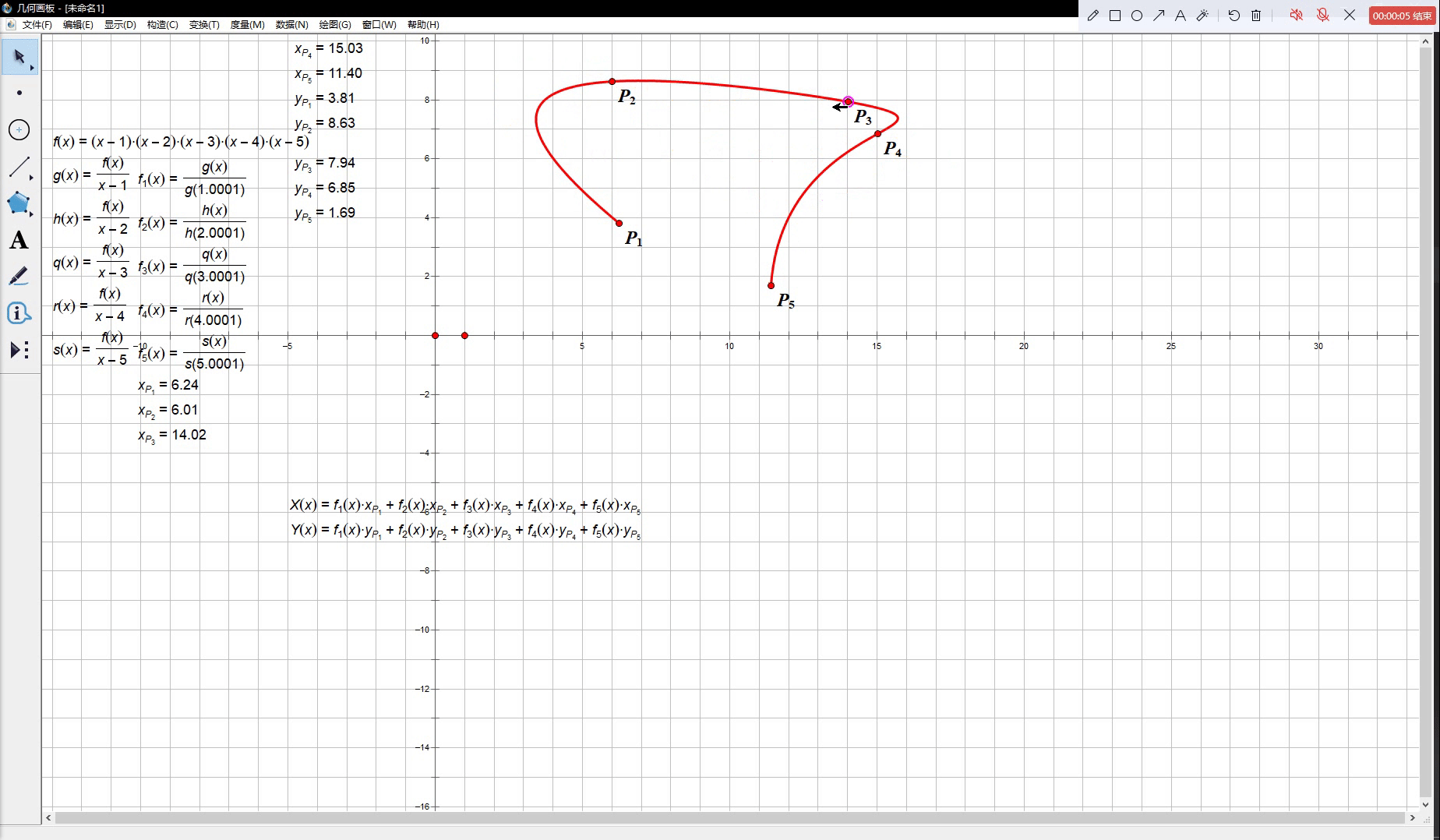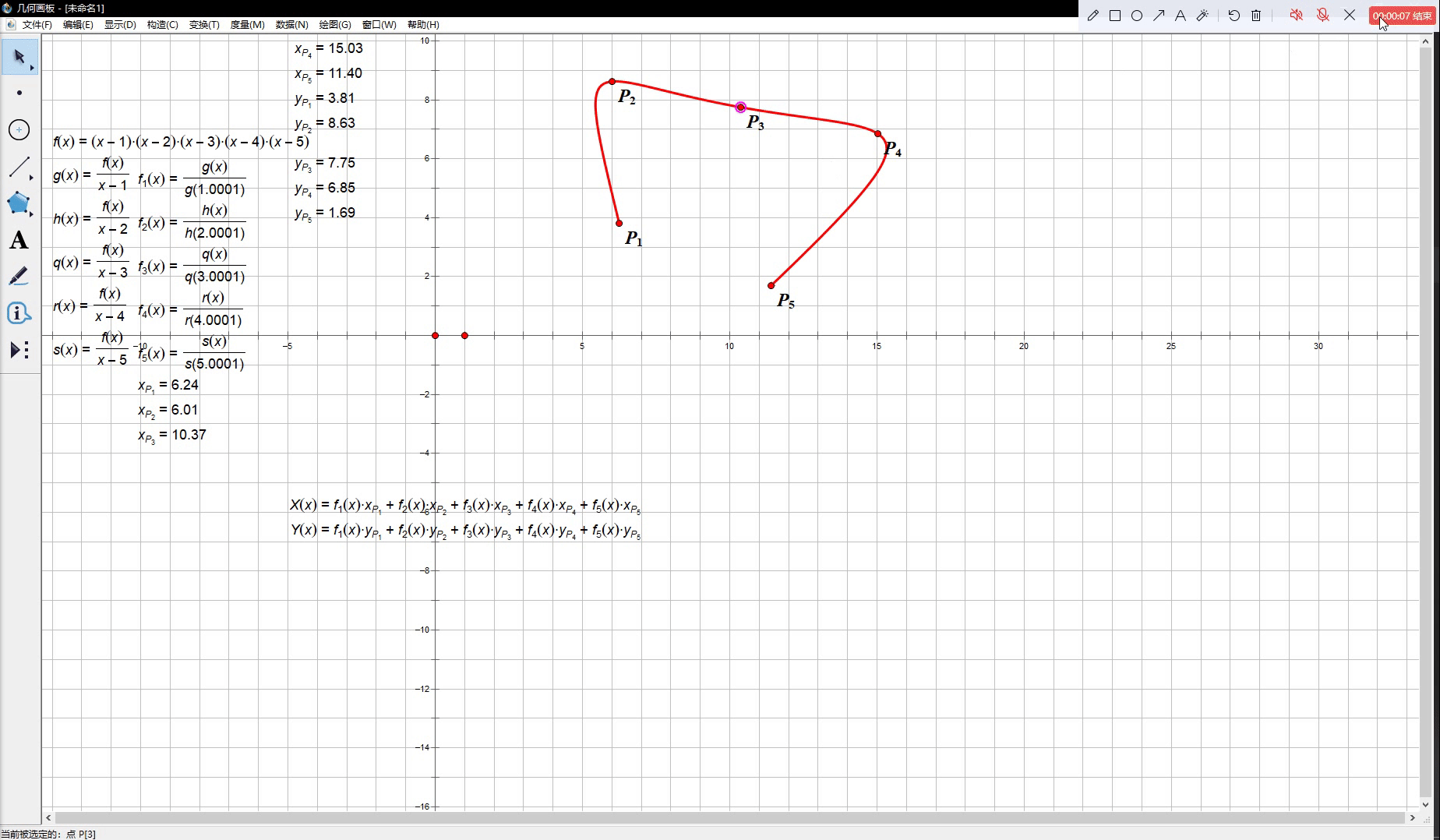
我们会看到，上图中红色的曲线确实忠实地穿过了 $P_1,P_2,\cdots ,P_5$ 这五个控制点，但是当我们改变其中一个点的坐标时，整条曲线都扭得很厉害，而这也正是插值曲线不适合做工业设计的原因。在大多数时刻我们都不仅需要曲线经过一些指定的定点，还希望曲线能在控制点变化时尽可能保持一个较为稳定的形态，否则我们将很难实现对曲线形状的自由控制。

但拉格朗日插值曲线也有它的优势，一方面他是插值曲线，能够通过指定的所有控制点，而拟合曲线只能近似通过某些控制点。另一方面就是拉格朗日插值曲线无穷阶可导连续，而这一点是一般的分段函数很难实现的。