线性代数的本质1

原创

已于 2022-02-04 17:18:32 修改 · 1.1k 阅读

4 ·

CC 4.0 BY-SA版权

文章标签：

#线性代数 #机器学习 #矩阵

于 2022-02-02 19:04:52 首次发布

干货满满~昨天停更了，因为机器学习白板推导听不明白了。。所以赶紧补补线性代数的课，二刷《线性代数的本质》，内容不难，很有助于打开思维。系列文章会尽量把精华都摘下来，有理解不当处欢迎指出。有兴趣的同学也可以直接去刷视频https://www.bilibili.com/video/BV1ys411472E?p=1http://link

向量究竟是什么？

在线性代数中，最基础最根源的组成部分就是向量，向量的加法和向量的乘法贯穿线性代数始终。而向量的定义，主要有三种角度的说法：

1）物理视角——向量是空间中的箭头，只要确定了它的长度和方向不变，就可以任意移动该向量而保持不变。

2）计算机视角——向量是有序的数字列表，在解决具体问题时选取不同的特征作为列表进行计算。

3）数学角度（抽象）——只要保证两个向量相加以及数字与向量相乘有意义，向量可以是任何东西。

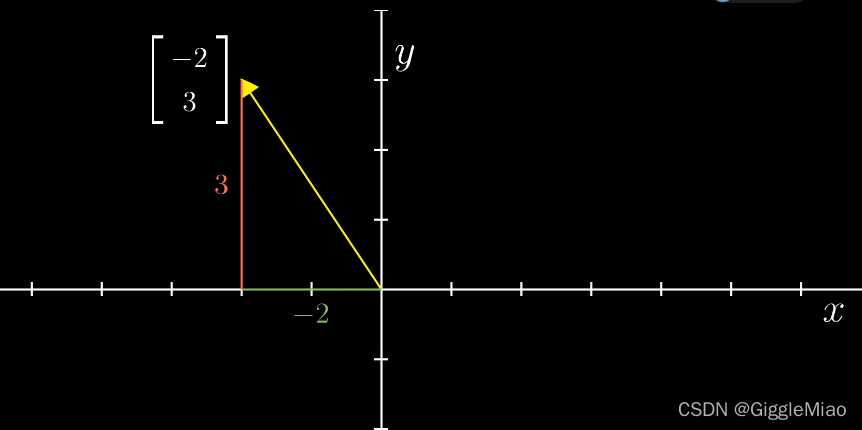
在“向量是有序的数字列表”中，如上图中黄色箭头表示的向量，第一个数告诉你从原点处沿着x轴走了多远，第二个数告诉你在此基础上沿着平行于y轴的方向走了多少。其中正数代表向右移动，负数代表向左移动。并且在线性代数中，一般默认向量的起源在原点。并且为了和坐标中的点(-2,3)进行区分，通常竖着写来表示向量 $\begin{bmatrix} -2\\ 3 \end{bmatrix}$ 。

每一对这样的数 $\begin{bmatrix} x\\ y \end{bmatrix}$ 给出唯一一个向量，每一个向量恰好对应唯一一对数 $\begin{bmatrix} x\\ y \end{bmatrix}$ 。

向量的加法 $\vec{v}+\vec{w}$ ：

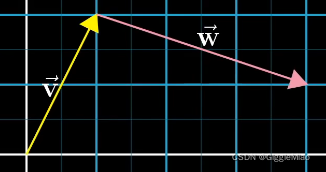
1）平移其中一个向量，使它的起点与另一个向量的终点重合：

2）然后从固定不动的向量起点出发，指向第平移向量的终点，此时构成的新向量就是 $\vec{v}+\vec{w}$ 的和。：

3）从“计算”的角度认为向量加法就是把对应项相加：

向量的数乘 $k\vec{v}$ ：

向量乘以一个数k，即是对向量进行拉伸和压缩k倍，-k时进行反向。也可以说，数字在线性代数中起到的主要作用就是缩放向量。（线性代数中，“数字”和“标量”认为是一样的）

从“计算”的角度认为向量与标量（数字）相乘就是将向量中的每个分量与标量相乘。

我们看到的每一个点，其实都可以认为是以该点为终点，原点为起点的一个向量。