阅读笔记-贝叶斯优化 -kridging/DACE/Gaussian Process随机模型（计算实验设计与分析）

Design and Analysis of Computer Experiments

"贝叶斯优化是一种强大的策略，用于查找评估成本高昂的目标函数极值。当这些评估成本高昂、无法获得导数或当前问题是非凸时，它特别有用"

在 Jones 等人之后，贝叶斯优化（BO) 在工程领域变得流行起来, 引入了高效全局优化（EGO).目前贝叶斯优化广泛用于深度学习超参优化。

虽然这是一篇古老的文章，发表为1989年，但是如果想学习随机优化，计算实验和优化，以及目前比较火的深度学习超参优化的贝叶斯优化，这是奠定基础的一篇文章。 该文章目前有7000多的引用。同时这篇paper的coathor 在10年后1998年发表了EGO算法的paper。

1. 介绍和背景

计算机建模正在革命性地改变科学研究，因为许多复杂的过程在实验上进行物理实验会耗费过多时间。本文提出了一种方法，将计算机实验的确定性输出视为随机过程进行建模，从而为设计实验和进行有效预测提供统计基础。

本文回顾了1989年之前计算机实验取得的进展。他们提出了许多应用程序来说明计算机实验的三个主要目标，包括：

a.预测未测试输入的响应变量，

b.优化响应的功能输出，

c.以及调整计算机模型以匹配物理数据

此外，本文讨论了统计在建模确定性计算机模型中的作用，并对比了计算机实验和物理实验之间的区别。其中一个关键区别是计算机实验中不存在随机误差（或噪声）。所有的误差均来自于模型误差，因为计算实验的输出是确定性的。

2. 建模和预测

计算实验的建模是通过随机过程实现实现的。确定性的响应变量 y(x) 被视为随机函数 Y(x) 的实现。模型的结构可以被看作是：响应变量= 线性模型 + 偏离量，即，

其中，随机过程 Z(•) 表示系统偏离假定简单回归模型的程度。假定 Z(•) 的均值为零，协方差结构与响应变量的平滑度相关。Z(w) 和 Z(x) 之间的协方差可以写成。 其中，R(w,x) 是相关性（注：为简化起见，本文摘要中的符号与原始论文中的符号一致）。

采用了空间统计学的kriging模型，通过运用最佳线性无偏预测器（BLUP）最小化均方误差（公式2）来导出未测试点 x 对应的响应变量Y(x) 的预测量 ：

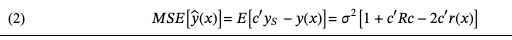
无偏性约束为 F′c = f(x) ，并使用拉格朗日乘数 λ 进行约束最小化 MSE，那么 BLUP 的系数 c 必须满足以下条件：

将约束（3）代入（2），MSE 也可以写成

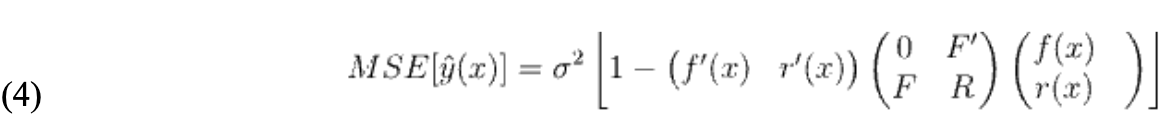
需要指定相关性 R(w,x) 才能计算上述数量。d 维相关性 R(w,x) 定义为一维相关性的乘积，即。以下表格1显示了本文提供的平滑相关函数：

Correlation	Form
Special weighted correlation	[Equation], where 0<p<2
Product of linear correlations
Cubic correlation on the unit cube	stationary for certain choice of aj and bj

随机过程模型的参数有𝛽𝑠、𝜎2和相关性参数𝜃𝑠和p需要被估计。最大似然估计（MLE）用于估计这些参数。如果给定相关性的参数，可以通过closed-form来推算𝛽𝑠和𝜎2的估计值。𝛽和𝜎2的MLE估计如下

𝛽𝑠和𝜎2的估计是间接的，因为它们必须与相关性参数𝜃𝑠和p的估计结合起来。通过上述（5）和（d），MLE问题被转化为最小化。

3. 设计准则和算法

论文讨论了三种不同的准则,来选择实验区域𝜒中的设计：综合均方误差（IMSE）、最大均方误差（MMSE）和熵。这些准则基于随机过程的后验协方差。

综合均方误差（IMSE）是通过给定的权重函数𝜙(𝑥)来最小化（7）来选择设计。

最小化的目标函数为：

其中，𝜙𝑥是权重函数，可以根据特定的应用程序选择。

最大均方误差（MMSE)通过优化 （8）选择设计

熵通过最小化预期后验熵𝐸(−log 𝑔)来选择设计，其中g表示给定Ys的Y(•)在上的条件密度。这个准则最初是在贝叶斯设计中提出的，后来被用于计算机实验设计中，以量化“信息量”。

设计构建的算法可以分为三组：单阶段方法、无数据适应的顺序方法和有数据适应的顺序方法。单阶段方法同时优化所有n个设计点，采用标准的优化技术，例如拟牛顿方法和交换算法，如模拟退火算法。相比之下，顺序设计将实验区域划分为几个子区域（或盒子），并确定对IMSE贡献最大的盒子。然后添加一个最能有效地减少该盒子贡献的数据点。

4. 结论

本文从多个角度讨论了开放的统计问题，例如由于计算运行时间而导致的模拟器复杂性、不能充分表征的计算机模型或高维输入、模型参数估计的可变性、设计算法中的计算挑战和数值误差、关于替代相关函数和回归结构的效率鲁棒性，以及来自Kriging方法中随机过程Z（•）的半方差函数。尽管存在这些挑战，但本文提出的计算机实验随机模型有效地量化了未观察到响应变量的不确定性，并呈现了一种设计和分析的高效框架，展示了它在各种应用中的价值。