本专栏是笔者主编教材(图0所示)的电子版,依托简易的元器件和仪表安排了30多个实验,主要面向经费不太充足的中高职院校。每个实验都安排了必不可少的【预习知识】,精心设计的【实验步骤】,全面丰富的【思考习题】。因此,对于开展电子技术教学犯愁的师生,本专栏应该能够帮到你们。

实验23 RL 串联电路
【实验目的】
- 学会从 RL 串联电路中的电压测量计算感抗。
- 会画 RL 串联电路的阻抗和电压相量图。
- 学会测量串联电路相位差的方法。
【预习知识】
当一个正弦信号加进线性串联电路中时,电流和电压的相位关系由电路中的元件决定。电阻上的电压和电流是同相位的,电容上的电流超前于电压 90°,而对于电感,则是电压超前于电流 90°。有个英文短句可以帮助你记忆它们的关系:ELI is the ICEman(伊莱是冰人——X战警中的一名超级英雄)。E 代表电压,I 代表电流,L 和 C 分别代表电感和电容。
RL 串联电路的原理图和相量图如图 1 所示,如同 RC 串联电路一样,总阻抗相量由电阻相量和电抗相量按照复数求和的方式得到。图中的数据是为了便于计算而给出的,串联电路选择电流作为参考相量是合适的,其大小为 1.0mA。电流相量与阻抗相量相乘便得到了电压相量。
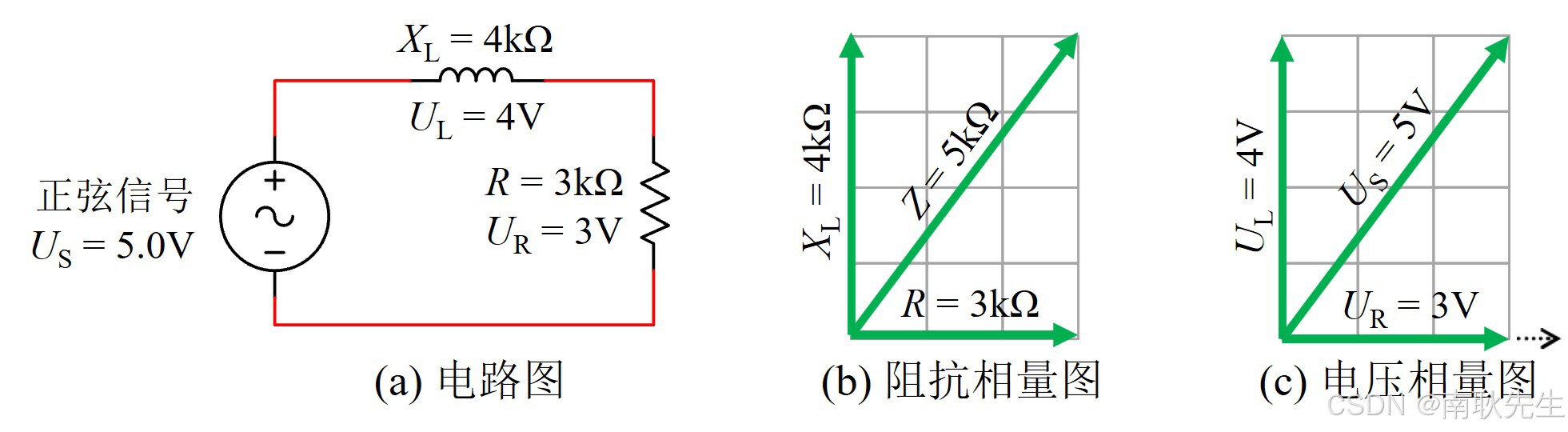
在本实验中,我们将学习如何测量相位角。实际的电感器本身是带有小的串联电阻,因此会影响电路的相位角。这里我们使用一个较大的串联电阻,以避免电感本身电阻引起的误差。
【实验元件与仪器】
- 1.0kΩ 电阻 1 支
- 10mH 工字电感 1 支
- 函数信号发生器 1 台
- 示波器 1 台
【操作内容及步骤】
1. 测量一下标称 1.0kΩ 电阻的实际阻值,记录表 1 中。如果条件允许(实验室配有 RLC 电桥),再测量一下标称 10mH 电感的实际电感量。如果没有条件,就使用标称值。
2. 本实验的测试电路如图 2 所示。完成连线后,设置函数发生器的输出为正弦波,频率 25kHz,峰峰值 3.0V,无直流电压偏置。将该信号接入示波器的 CH1 通道进行验证。注意,本实验接下来所有的测量值都取峰峰值。
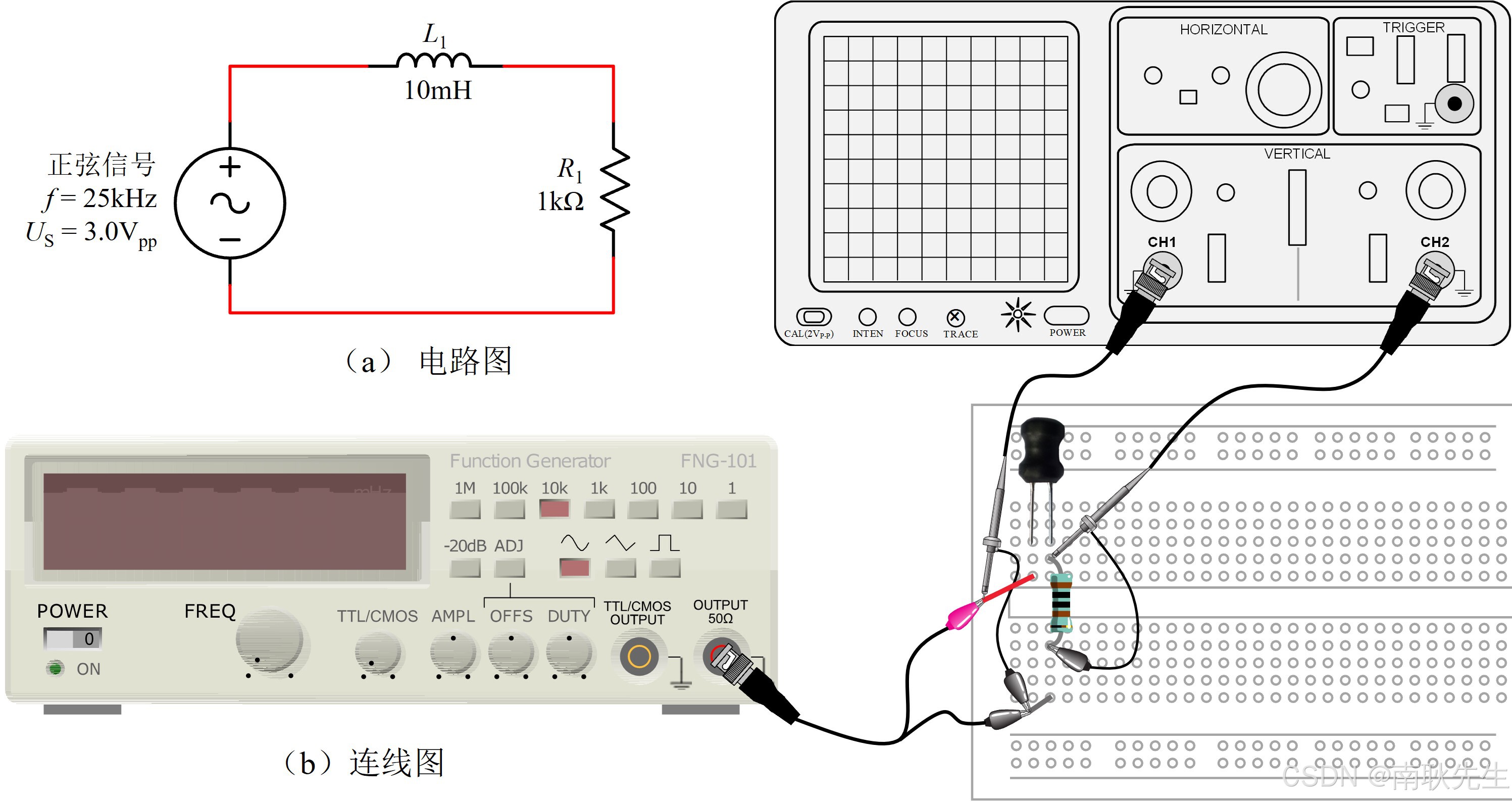

3. 使用示波器的 CH2 通道观察电阻上的信号 。由于电感是未接地元件,因此需要使用信号差的方式观察电感上的信号
。将这两个参数的峰峰值记录在表 2 中。
4. 在电阻上通过欧姆定律计算出电流 ,取峰峰值记录在表 2 中。
5. 在电感上通过欧姆定律计算出感抗 ,记录在表 2 中。
6. 计算 RL 串联电路的总阻抗 ,记录在表 2 中。
7. 根据两张表中的实验数据,在图 3 中绘制 25kHz 下的阻抗相量图和电压相量图。
8. 根据电压相量图计算 和
的相位差,可由以下公式得到,将结果记录在表 3 中:
9. 这一步,我们通过两种方法在示波器上读出 和
的相位差,读数记录在表 3 中。
方法1:
a) 保持图 2 中示波器通道的接线方式,调整示波器控件使 CH1 通道的 信号在屏幕上呈现1~2个完整且稳定的周期,并读出周期 T,记录在表 3 中,下面会用到。
b) 将示波器设置为同时查看两个通道(勿将 CH2 通道反向)。首先,通过调整 VOLTS/DIV 的内外圈旋钮和 VERTICAL POSITION 旋钮,使两个波形对齐并呈现相同幅度,如图 4(a)所示。然后,再调节 TIME/DIV 控件将波形展开,以更准确地读取两个信号的时间差 ,如图 4(b)所示,将读数记录表 3 中。
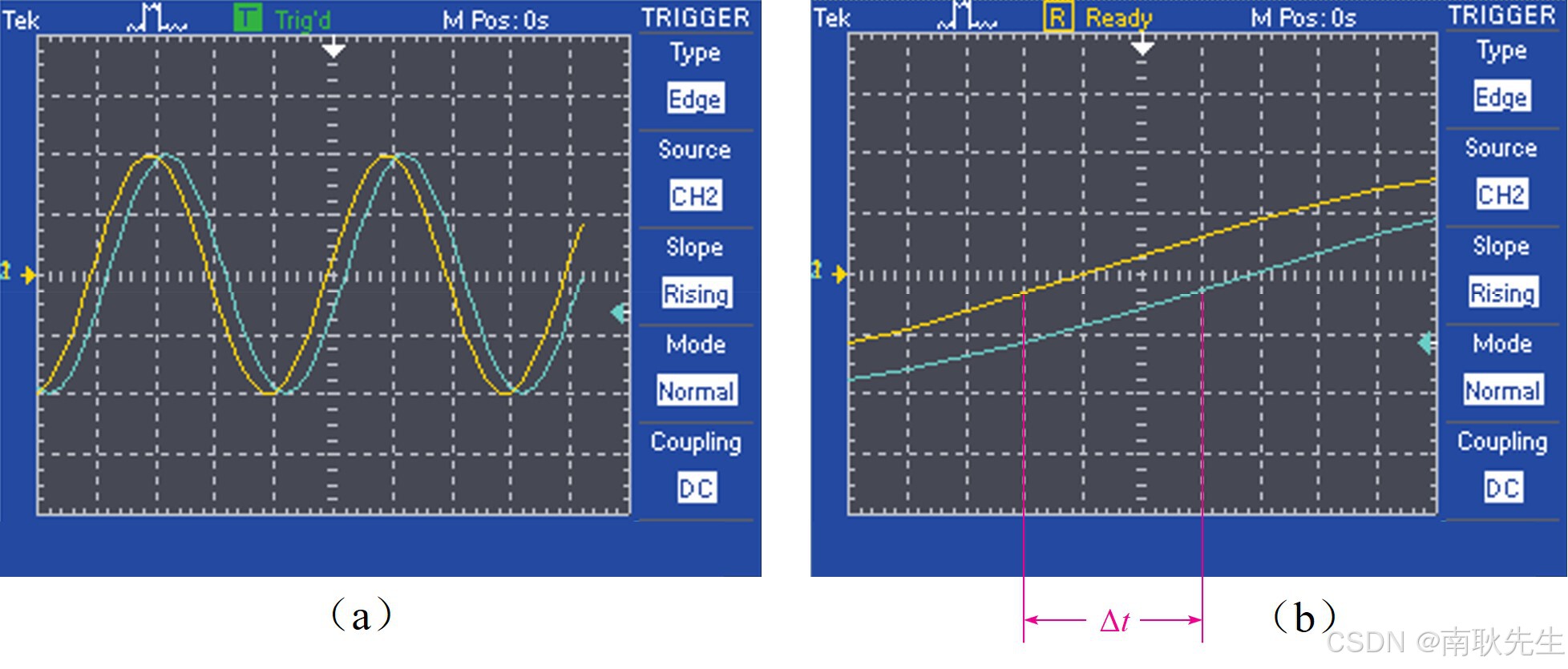
c) 通过下面公式可以计算出两个信号的相位差,计算结果记录在表 3 的“方法1”所在列。
方法2:
a) 上一个方法需要先测量出时间差,再换算出相位差。而在本方法中,能够直接从波形读出度数。保持示波器连线不变,先只显示 CH1 通道信号。调节 TIME/DIV 和 SWP.VAR. 控件使屏幕上只呈现一个完整周期,这样的话水平方向每格代表 36°。
b) 接下同时打开示波器两个通道,与上一个方法一样,把两个信号的幅度调的一致。
c) 根据两个波形水平方向相距的格子数乘上 36°,计算得到相位差,将结果记录在表 3 的“方法2”所在列。

【实验思考与讨论】
1. 本实验中,如果频率增加,总阻抗如何变化?如果电感变大,总阻抗又如何变化?
2. 本实验中,如果频率增加,相位差如何变化?如果电感变大,相位差又如何变化?
3. 根据表 3 中的数据,回答以下几个问题:
a) 相位差的计算值与方法 1 的测量值之间的误差(百分比)为多少?
b) 相位差的计算值与方法 2 的测量值之间的误差(百分比)为多少?
c) 那种方法的测量结果更精确?请解释原因。
4. RL 串联电路的临界频率出现在电阻与感抗相等的时候,即 。由于
,因此可以很容易的计算出临界频率:
根据本实验电路中的参数计算临界频率,并计算该频率下 和
的相位差。
5. 一个 RL 串联电路中,R = 100Ω,L = 1.0H,工作频率 f = 50Hz。如果电阻上压降的有效值为 3.0V,请计算:
a) 电感电流 I = ________ b) 感抗 = ________ c) 电感的压降
= ________
d) 信号源电压 = ________ e)
与
的相位差
= ________
【实验拓展与延伸】
还有一种测量相位差的方法——借助利萨茹曲线。数学上,利萨茹曲线是两个沿着互相垂直方向的正弦振动的合成的轨迹。两个幅度相等且相位一致的信号将合成产生一条 45° 的线段。如果两个信号的幅度相同,相位差 90°,合成之后将以圆的形式出现。其他相位差合成的图形则为椭圆,如图 5 所示,其相位差可由以下公式计算得到:
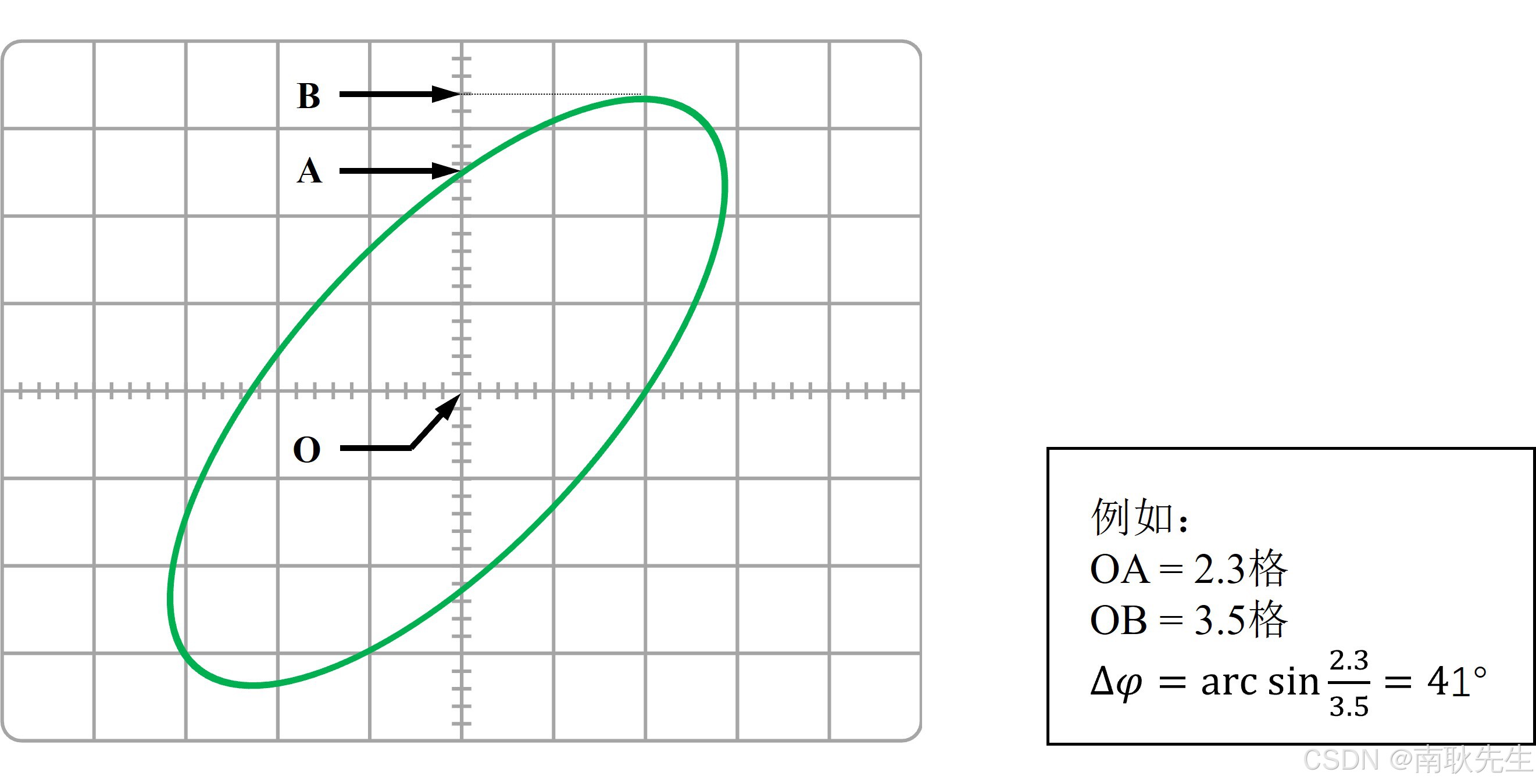
根据上图示意测量本实验中的相位差。测量时需要注意几点:①两信号的幅度必须一致;②波形必须在屏幕上居中;③将 TIME/DIV 控件调至 X-Y 挡位。
(本文完)


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










