jzoj4216. 【NOIP2015模拟9.12】平方和(splay+码量)

Description
给出一个N个整数构成的序列，有M次操作，每次操作有一下三种：
①Insert Y X，在序列的第Y个数之前插入一个数X；
②Add L R X，对序列中第L个数到第R个数，每个数都加上X；
③Query L R，询问序列中第L个数到第R个数的平方和。

Input
第一行一个正整数N，表示初始序列长度。
第二行N个整数Ai，表示初始序列中的数。
第三行一个正整数M，表示操作数。
接下来M行，每行一种操作。

Output
对于每一个Query操作输出答案。由于答案可能很大，请mod 7459后输出。

Sample Input
5
1 2 3 4 5
5
Query 1 3
Insert 2 5
Query 2 4
Add 5 6 7
Query 1 6

Sample Output
14
38
304
样例解释：
第二次操作后的序列：1，5，2，3，4，5。
第四次操作后的序列：1，5，2，3，11，12。

Data Constraint
30%的数据满足N≤1,000，M≤1,000。
另外20%的数据满足N≤100,000，M≤100,000，且不存在Insert操作。
100%的数据满足N≤100,000，M≤100,000，且Add和Insert操作中|X|≤1000，|Ai|≤1000。

---

如果这题没有插入操作，可以直接用线段树做。

方法

①线段树预处理出空位，离线 （不讲）
②splay

splay定义

splay其实就是二叉排序树的优化。
二叉排序树：
一种特殊的二叉树，每个子树的左节点的关键字都小于根节点，右节点都大于根节点。

splay的优点

时间空间优化，可以通过旋转来实现。
可以删除/插入/更改值。

旋转

分左旋和右旋两种。

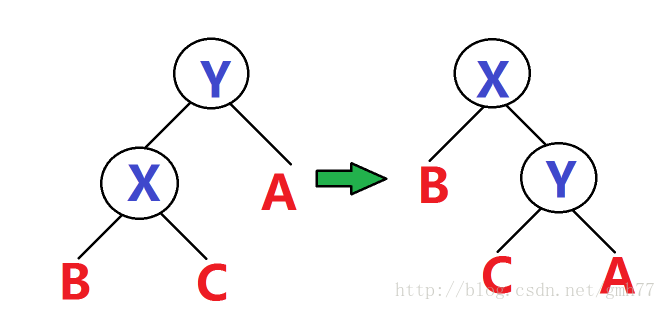
①右旋

②左旋

其实旋转操作很简单。。

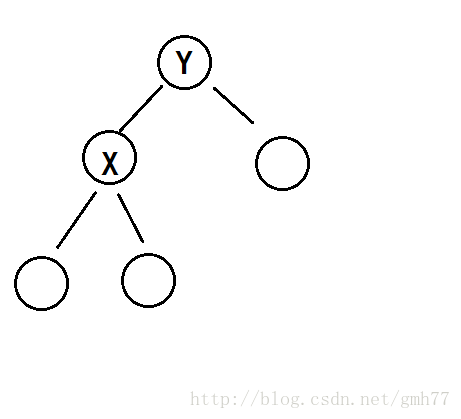
左旋：

由图得知，B < X < C < Y < A，
旋转后，树的形状改变，但是性质没有改变。
仍然是B < X < C < Y < A。

因为旋转后，Y变成X的子树。
所以只需让X认Y父为父，让Y认X为父，
因为X的右儿子被Y占据，所以把Y的左儿子设为C。

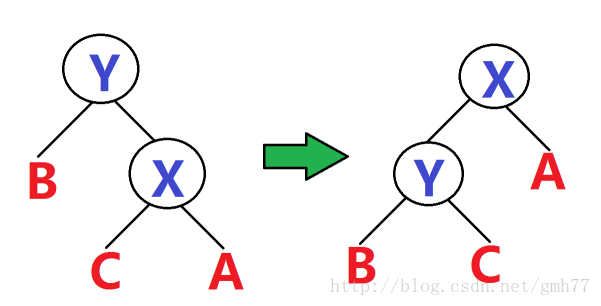
右旋：

同理。
不同是要把Y的右儿子设为C。

X是新父节点的左/右儿子要根据Y决定。

旋转的卵用

其实splay的核心思想，就是通过旋转，把某个节点转到另一个节点的下方，
从而进行一些更重要的操作。

还是旋转

如果经过一通**(这只是星号)乱转，有可能会变成这样一个情况：

平衡树将会由树退化成链。
这样平衡树的优势——logN的复杂度将会得不到体现。
所以旋转要用更科学的方法。

假设当前节点为X，要把X旋转到Z的下方：
①X的爷爷是Z
两种情况：

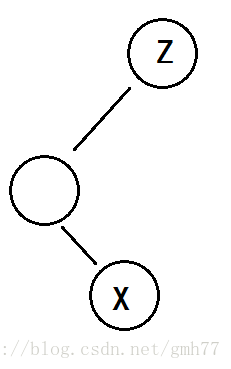
直接左旋。

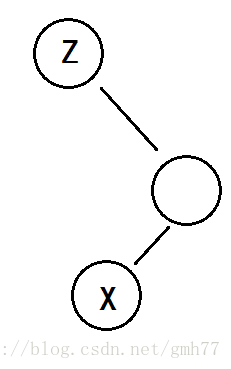
直接右旋。

②X的爷爷不是Z
两种：
一条链：

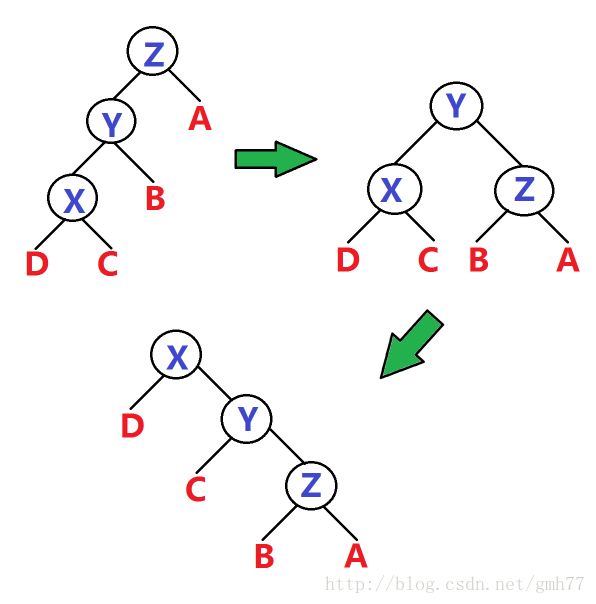
先旋转X的父节点，再旋转X。
反向同理。

如果直接二次旋X会变慢（10%左右，实测）
原理未知

折角：

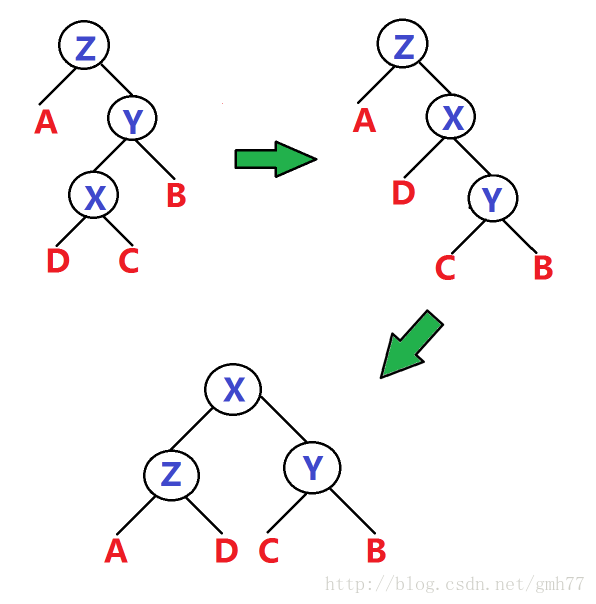
二连旋X。
如果旋转父节点，则X会不动。

反向同理。

旋转模板（通用）

（T数组表示树，T[i,1]表示左儿子编号，T[i,2]表示右儿子编号，没有加数据更新）：

左旋：

procedure left(x:longint);
var
        y,z:longint;
begin
        y:=f[x];//取得父节点
        z:=f[y];
        f[x]:=z;//修改父节点
        f[y]:=x;
        if z=0 then
        root:=x//修改根，本题用不上
        else
        begin
                if t[z,1]=y then//修改X新父节点的儿子
                t[z,1]:=x
                else
                t[z,2]:=x;
        end;
        if t[x,1]>0 then//修改X左儿子父亲
        f[t[x,1]]:=y;
        t[y,2]:=t[x,1];//修改Y右儿子，设为X的左儿子
        t[x,1]:=y````
//修改X的左儿子为Y
end;

右旋

跟左旋类似，不多说。

procedure right(x:longint);
var
        y,z:longint;
begin
        y:=f[x];
        z:=f[y];
        f[x]:=z;
        f[y]:=x;
        if z=0 then
        root:=x
        else
        begin
                if t[z,1]=y then
                t[z,1]:=x
                else
                t[z,2]:=x;
        end;
        if t[x,2]>0 then
        f[t[x,2]]:=y;
        t[y,1]:=t[x,2];
        t[x,2]:=y;
end;

连旋

procedure splay(x,y:longint);
var
        i:longint;
begin
        if (x=y) or (x=0) then
        exit;
        while f[x]<>y do
        begin
                if f[f[x]]=y then//单旋
                begin
                        if t[f[x],1]=x then
                        right(x)
                        else
                        left(x);
                end
                else
                begin//双旋
                        if (t[f[f[x]],1]=f[x]) and (t[f[x],1]=x) then//二连右
                        begin
                                right(f[x]);
                                right(x);
                        end
                        else
                        if (t[f[f[x]],2]=f[x]) and (t[f[x],2]=x) then//二连左
                        begin
                                left(f[x]);
                                left(x);
                        end
                        else
                        if (t[f[f[x]],1]=f[x]) and (t[f[x],2]=x) then//左右
                        begin
                                left(x);
                                right(x);
                        end
                        else
                        if (t[f[f[x]],2]=f[x]) and (t[f[x],1]=x) then//右左
                        begin
                                right(x);
                                left(x);
                        end;
              end;
        end;
end;

查找操作

通过关键字查找，利用二叉排序树的性质，大的在右，小的在左，一路找下去。

这是个难点。
先想想，如果把每个节点的大小明确地记录下来，那么
每次插入节点过后，原来在节点后的点的编号都要加一。
这样太eggache了

作为高 (gǎo) 级 (jī) 算法的splay，其实早已给出了解决方案。

举个例子：

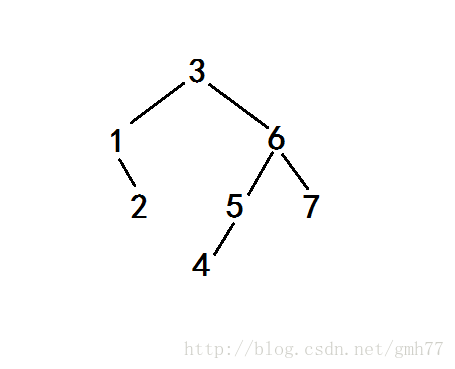
比如，我要从根节点开始寻找第2小的数(假设是节点2)。

---

根据二叉排序树的性质可得，根节点左子树的节点都比根节点关键字的值小，右子树的都比根节点大。

设size[i]表示以i为根的子树节点个数。
则根节点是第几小的数就是size[根的左儿子]+1（根据性质可得）。
第几小既是它的关键字。

那么我们只需把查找的数和当前查找到的节点作比较，如果关键字更小就在左子树，更大就在右子树，相同就找到了。

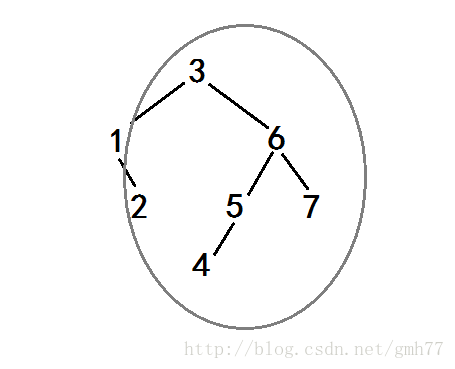
还是刚刚那个例子，由于2<(2+1)，所以2在3的左子树上。

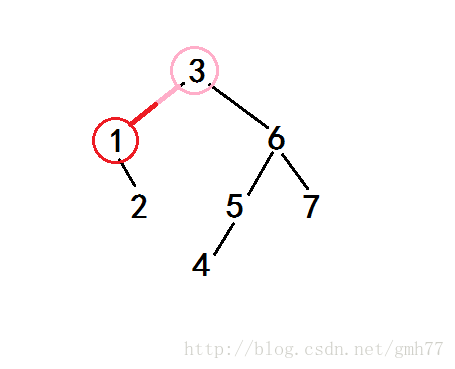
因为我们要求的是第几小的数，所以当前节点的右子树和父节点们的右子树们（灰圈）

都没有任何卵用

所以可以直接往下找。

---

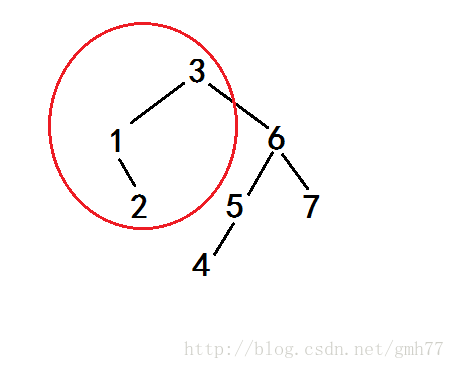
又比如，刚刚那个图，我要求7的位置。
计算后发现，要向右走（同上）。

但是走完以后发现，我们搜索的子树范围减小了，因为前面有比它小的数（红圈），所以要减去（size[左儿子]+1）

其实就是把走之前的节点的关键字减去。

查找模板

function find(x,s:longint):longint;
begin
        if s=size[t[x,1]]+1 then//找到
        exit(x)
        else
        if s<size[t[x,1]]+1 then//在左子树
        exit(find(t[x,1],s))
        else
        exit(find(t[x,2],s-size[t[x,1]]-1));//在右子树（要减去当前关键字）
end;

插入操作（1/3）

因为一个**的原因电脑崩溃要重打。。。。

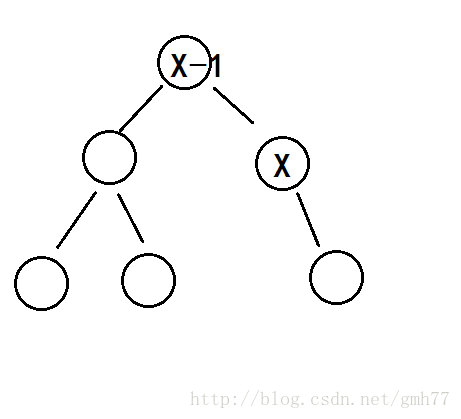
其实很简单（条件是上文提到的所有操作都打对），假设要再X前面插入一个节点，先用splay+find把X-1拖到根，再把X拖到X-1的右儿子。

如果不出意外（各种蜜汁错误）就是这样：

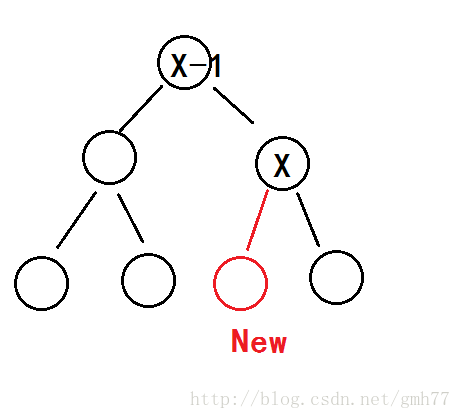
因为X-1和X之间没有其它数，所以此时的X也没有左儿子。
直接在X的左儿子新建节点。

解决了三个操作之一。

区间加（2/3）

直接打lazy-tag标记。
好吧，lazy-tag就是把要加的数先存下来，等到计算到它时再加。

大致同线段树。

再旋转/查找/区间加时下传标记。

每次把L-1拉到根，再把R+1拉到L-1的右子树，那么R+1的左子树就是L~R。
直接在它的左儿子上打标记。

又是三分之一。

询问（3/3）

大同区间加，把L-1拉到根，再把R+1拉到L-1的右子树，那么R+1的左子树就是L~R。

直接输出就行了。

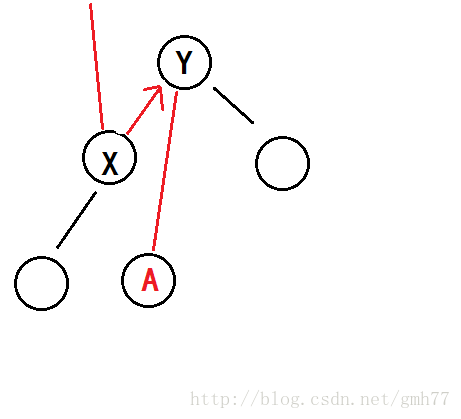
又是旋转

这是很重要的一点。

每次旋转后，X和Y的数据都会有改变。
比如这样：

Y的数据变成右子树+A点数据+自己。
X的数据加上新的Y-A点数据

仔细考虑/测试一下。
否则又是各种蜜汁错误

计算答案

这跟树没有任何关系。

(a+b)^2=a^2+b^2+2ab
Σ(a+b)^2=Σa^2+b^2*size+2bΣa

理解理解。

最终代码

const
        md=7459;
var
        t:array[0..200000,0..2] of longint;
        f:array[0..200000] of longint;
        a:array[0..200000] of longint;
        size:array[0..200000] of longint;
        num:array[0..200000] of longint;
        num2:array[0..200000] of longint;
        put:array[0..200000] of longint;
        bj:array[0..200000] of longint;
        n,m,i,j,k,l,x,y,z,root:longint;
        ch:char;
        s:string;
procedure look;//查看各种数据，测试用。（可删）
var
        i:longint;
begin
        writeln('Root:',root);
        for i:=1 to n do
        writeln('Data:',t[i,0],' Left:',t[i,1],' Right:',t[i,2],' Father:',f[i],' Size:',size[i],' X:',num[i],' X^2:',num2[i],' Lazy BJ:',bj[i]);
end;
procedure downdata(x:longint);//下传数据
begin
        if bj[x]=0 then
        exit;
        if t[x,1]>0 then
        bj[t[x,1]]:=bj[t[x,1]]+bj[x];
        if t[x,2]>0 then
        bj[t[x,2]]:=bj[t[x,2]]+bj[x];
        num2[x]:=(((num2[x]+((bj[x]*bj[x]) mod md)*size[x]) mod md)+2*bj[x]*num[x]) mod md;
        num[x]:=num[x]+bj[x]*size[x];
        t[x,0]:=t[x,0]+bj[x];
        bj[x]:=0;
end;
procedure right(x:longint);//右旋
var
        y,z:longint;
begin
        downdata(x);
        y:=f[x];
        z:=f[y];
        f[x]:=z;
        f[y]:=x;
        if z=0 then
        root:=x
        else
        begin
                if t[z,1]=y then
                t[z,1]:=x
                else
                t[z,2]:=x;
        end;
        size[y]:=size[t[y,2]]+1+size[t[x,2]];//更新
        size[x]:=size[x]+size[y]-size[t[x,2]];
        num[y]:=(num[t[y,2]]+t[y,0]+num[t[x,2]]) mod md;
        num[x]:=(num[x]+num[y]-num[t[x,2]]) mod md;
        num2[y]:=(num2[t[y,2]]+t[y,0]*t[y,0]+num2[t[x,2]]) mod md;
        num2[x]:=(num2[x]+num2[y]-num2[t[x,2]]) mod md;
        if t[x,2]>0 then
        f[t[x,2]]:=y;
        t[y,1]:=t[x,2];
        t[x,2]:=y;
end;
procedure left(x:longint);//左旋
var
        y,z:longint;
begin
        downdata(x);
        y:=f[x];
        z:=f[y];
        f[x]:=z;
        f[y]:=x;
        if z=0 then
        root:=x
        else
        begin
                if t[z,1]=y then
                t[z,1]:=x
                else
                t[z,2]:=x;
        end;
        size[y]:=size[t[y,1]]+1+size[t[x,1]];
        size[x]:=size[x]+size[y]-size[t[x,1]];
        num[y]:=(num[t[y,1]]+t[y,0]+num[t[x,1]]) mod md;
        num[x]:=(num[x]+num[y]-num[t[x,1]]) mod md;
        num2[y]:=(num2[t[y,1]]+t[y,0]*t[y,0]+num2[t[x,1]]) mod md;
        num2[x]:=(num2[x]+num2[y]-num2[t[x,1]]) mod md;
        if t[x,1]>0 then
        f[t[x,1]]:=y;
        t[y,2]:=t[x,1];
        t[x,1]:=y;
end;
procedure splay(x,y:longint);//各种旋
var
        i:longint;
begin
        if (x=y) or (x=0) then
        exit;
        while f[x]<>y do
        begin
                if f[f[x]]=y then
                begin
                        if t[f[x],1]=x then
                        right(x)
                        else
                        left(x);
                end
                else
                begin
                        if (t[f[f[x]],1]=f[x]) and (t[f[x],1]=x) then
                        begin
                                right(f[x]);
                                right(x);
                        end
                        else
                        if (t[f[f[x]],2]=f[x]) and (t[f[x],2]=x) then
                        begin
                                left(f[x]);
                                left(x);
                        end
                        else
                        if (t[f[f[x]],1]=f[x]) and (t[f[x],2]=x) then
                        begin
                                left(x);
                                right(x);
                        end
                        else
                        if (t[f[f[x]],2]=f[x]) and (t[f[x],1]=x) then
                        begin
                                right(x);
                                left(x);
                        end;
                end;
        end;
end;
function find(x,s:longint):longint;//查找
begin
        if t[x,1]>0 then
        downdata(t[x,1]);
        if t[x,2]>0 then
        downdata(t[x,2]);
        if s=size[t[x,1]]+1 then
        exit(x)
        else
        if s<size[t[x,1]]+1 then
        exit(find(t[x,1],s))
        else
        exit(find(t[x,2],s-size[t[x,1]]-1));
end;
begin
        readln(n);
        root:=1;
        t[1,2]:=2;
        for i:=1 to n do
        begin
                read(a[i+1]);
                f[i+1]:=i;//建树
                t[i+1,0]:=a[i+1];
                t[i+1,2]:=i+2;
                size[i+1]:=n+2-i;
        end;
        n:=n+2;
        for i:=n-1 downto 1 do
        begin
                num[i]:=(num[i+1]+a[i]) mod md;//初始化
                num2[i]:=(num2[i+1]+a[i]*a[i]) mod md;
        end;
        size[1]:=n;//个数
        size[n]:=1;
        f[n]:=n-1;
        readln(m);
        for i:=1 to m do
        begin
                s:='';
                read(ch);
                while ch<>' ' do
                begin
                        s:=s+ch;
                        read(ch);
                end;
                read(x,y);
                if s[1]='A' then
                read(z);
                readln;
                case s[1] of
                        'A'://查找
                        begin
                                j:=find(1,x);
                                k:=find(1,y+2);
                                splay(j,1);
                                splay(k,j);
                                bj[t[k,1]]:=bj[t[k,1]]+z;
                                downdata(t[k,1]);
                        end;
                        'I'://插入
                        begin
                                j:=find(1,x);
                                k:=find(1,x+1);
                                splay(j,1);
                                splay(k,j);
                                inc(n);
                                t[n,0]:=y;
                                t[n,1]:=0;
                                t[n,2]:=0;
                                f[n]:=k;
                                t[k,1]:=n;
                                num[n]:=y;
                                num2[n]:=y*y mod md;
                                size[n]:=1;
                                num[j]:=(num[j]+y) mod md;
                                num[k]:=(num[k]+y) mod md;
                                num2[j]:=(num2[j]+y*y) mod md;
                                num2[k]:=(num2[k]+y*y) mod md;
                                inc(size[j]);
                                inc(size[k]);
                        end;
                        'Q'://询问
                        begin
                                j:=find(1,x);
                                k:=find(1,y+2);
                                splay(j,1);
                                splay(k,j);
                                writeln((num2[t[k,1]]+md) mod md);
                        end;
                end;
        end;
end.

参考资料：
http://blog.csdn.net/skydec/article/details/20151805
http://blog.csdn.net/cold_chair/article/details/72152376
http://blog.csdn.net/alan_cty/article/details/51220930
http://blog.csdn.net/Cold_Chair/article/details/71431490
http://blog.csdn.net/lyd_7_29/article/details/54292732
http://blog.csdn.net/jerrydung/article/details/7952460
(优化)