量化树形LSTM的实验评估

gold

于 2025-10-08 03:58:30 发布

阅读量611

点赞数 30

CC 4.0 BY-SA版权

文章标签：树形LSTM 量化层归一化

本文链接：https://blog.csdn.net/gold/article/details/152698148

量化树形LSTM的提出及其实验评估

一、引言

长短期记忆网络（LSTM）[1]是一种循环神经网络（RNN），在各种序列建模任务中取得了显著成果。然而，LSTM的结构是线性的，无法捕捉树形结构（如句子语法树）的信息。为了解决这一问题，提出了树形LSTM[2]，它能够更好地处理树形结构的信息。

此外，还有一种使神经网络紧凑的技术，称为量化。通过量化可以减小参数大小，或者通过优化计算过程来加速计算。

在本研究中，我们将树形LSTM与权重的量化函数结合，以减少参数大小。我们还验证了量化树形LSTM的准确率，并尝试对其进行了改进。

二. 相关工作

A. 树形LSTM

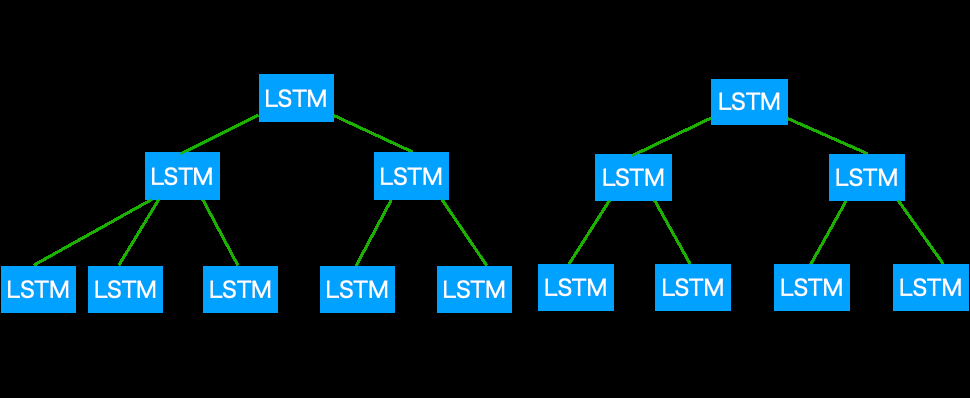
树形LSTM[2]是一种能够接收树结构信息的LSTM衍生模型，主要用于处理句子的任务，其输入为一个句子和一棵语法树的组合。树形LSTM有两种类型：子节点求和树形LSTM对子节点数量没有限制，且子节点的顺序无意义；二叉树形LSTM仅有两个子节点，且子节点的顺序（左、右）具有意义。图1表示了两种类型树形LSTM的结构，wi表示树形LSTM的一个输入。

示意图0

B. 量化

量化是一种将神经网络中的信息转换为较少比特数表示的方法。这种方法可以压缩模型的参数大小，并在优化计算方法的情况下加快计算速度。通常，神经网络中的信息以16或32比特进行处理，而量化则将其减少到1至8比特。

我们采用了以下用于量化的办法，这些是使用1或2比特的量化方法。

二值连接（BC）
三值连接（TC）
二值权重网络（BWN）
三值权重网络（TWN）

C. 层归一化

层归一化[5]将每一层的激活值归一化为零均值和单位方差。

$$
\text{LayerNorm}(a) = g \odot \frac{a - \mu \mathbf{1}}{\sigma} + b
$$

g和b表示增益和偏置参数。在激活a的元素上计算的均值µ和标准差σ。

III. 提出的方法

我们提出了将量化函数应用于树形LSTM权重的量化树形LSTM，并通过实验评估了哪种量化方法更有效。同时采用了层归一化以改善因量化导致的准确率下降问题。

$$
W_q = \text{Quantize}(W_f)
$$

$$
W_l = \text{LayerNorm}(W_q) \quad \text{(optional)}
$$

$W_f$, $W_q$, $W_l$分别表示全精度权重、量化后的权重和层归一化后的权重。Quantize函数从四种量化方法（BC, TC, BWN, TWN）中选择。

四、实验与结果

A. 任务

我们使用SICK语义相关性数据集[4]来评估所提出模型。SICK任务旨在预测一对句子的相似性得分，得分范围为[1, K]。

示意图1

图2表示SICK语义相关性数据集中数据的一个示例。我们首先使用树形LSTM为每个句子生成句子表示$h_L$和$h_R$，然后使用神经网络预测相似度得分$\hat{y}$：

$$
h_\times = h_L \odot h_R
$$

$$
h_+ = |h_L - h_R|
$$

$$
h_s = \sigma(W^{(\times)}h_\times + W^{(+)}h_+ + b^{(h)})
$$

$$
\hat{p}_\theta = \text{softmax}(W^{(p)}h_s + b^{(p)})
$$

$$
\hat{y} = r^T \hat{p}_\theta
$$

其中$r = {1, 2, \cdots, K}$。

B. 结果

我们使用皮尔逊相关系数和均方误差（MSE）作为评估指标。

表I CHILDSUM TREE-LSTM在SICK上的结果

	Loss	皮尔逊相关系数	MSE
全精度	0.09654	0.8669	0.2540
BC	0.1564	0.5742	0.6886
TC	0.1572	0.5524	0.7096
BWN	0.1281	0.7397	0.4698
TWN	0.1277	0.7431	0.4612
二值化卷积 (层归一化)	0.1181	0.7949	0.3965
三值化卷积 (层归一化)	0.1164	0.7946	0.3885
二值化权重网络 (层归一化)	0.1137	0.8018	0.3676
TWN（层归一化）	0.1182	0.7935	0.3972

表II 二值化树形LSTM在SICK上的结果

	Loss	皮尔逊相关系数	MSE
全精度	0.1112	0.8304	0.3179
BC	0.1725	0.4109	0.8569
TC	0.1706	0.4372	0.8422
BWN	0.1289	0.7384	0.4664
TWN	0.1350	0.7307	0.5253
BC（层归一化）	0.1255	0.7468	0.4549
TC（层归一化）	0.1241	0.7570	0.4446
二值化权重网络（层归一化）	0.1250	0.7491	0.4626
三值化权重网络（层归一化）	0.1261	0.7467	0.4657

在我们的实验中，将四种不同的量化方法（BC、TC、BWN、TWN）应用于两种类型的树形LSTM（ChildSum和Binary）。我们还尝试了添加层归一化。

从表I和表II可以看出，总体而言，应用量化后得分有所下降（尤其是在BC和TC中），但在应用层归一化后得分得到提升。此外，在SICK数据集上，子节点求和的得分优于二叉树结构。就单项得分而言，采用二值化权重网络并结合层归一化的子节点求和树形LSTM具有最高的准确率。

C. 层归一化的参数开销

下面将讨论添加层归一化后参数开销的问题。表示浮点精度所需的比特数为32比特，树形LSTM的门控机制数量为4个，输入和隐藏状态的维度分别设为x和h。因此，普通树形LSTM所需的比特数为$32 \times 4 \times (xh + hh + h)$比特，而m比特量化树形LSTM所需的比特数为$m \times 4 \times (xh + hh) + 32 \times 4 \times h$比特（以子节点求和为例）。由于添加层归一化的开销为$32 \times 16 \times h$比特，将层归一化应用于m比特量化树形LSTM时，所需参数数量为$m \times 4 \times (xh + hh) + 32 \times 20 \times h$比特。在本研究中，我们实验了$m = 1$或2，$x = 300$以及$h = 150$的情况，这意味着量化带来的参数规模缩减收益大于添加层归一化的开销。

五、结论

在本研究中，我们对树形LSTM的权重进行了量化，并实验评估了不同量化方法的有效性。结果表明，尽管其准确率不及全精度模型，但我们能够在保持一定程度准确率的同时减小参数大小。我们还确认，在所有量化模型中，采用二值化权重网络对子节点求和模型进行量化并应用层归一化后的模型准确率最高。未来，我们希望尝试其他量化方法，通过优化计算方式来加速计算，并验证该模型在小型设备上的运行情况。