数据结构和算法——Huffman树和Huffman编码

Huffman树是一种特殊结构的二叉树，由Huffman树设计的二进制前缀编码，也称为Huffman编码在通信领域有着广泛的应用。在word2vec模型中，在构建层次Softmax的过程中，也使用到了Huffman树的知识。

在通信中，需要将传输的文字转换成二进制的字符串，假设传输的报文为：“AFTERDATAEARAREARTAREA”，现在需要对该报文进行编码。

一、Huffman树的基本概念

在二叉树中有一些基本的概念，对于如下所示的二叉树：

• 路径

路径是指在一棵树中，从一个节点到另一个节点之间的分支构成的通路，如从节点8到节点1的路径如下图所示：

• 路径长度

路径长度指的是路径上分支的数目，在上图中，路径长度为2。

• 节点的权

节点的权指的是为树中的每一个节点赋予的一个非负的值，如上图中每一个节点中的值。

• 节点的带权路径长度

节点的带权路径长度指的是从根节点到该节点之间的路径长度与该节点权的乘积：如对于1节点的带权路径长度为：2。

• 树的带权路径长度

树的带权路径长度指的是所有叶子节点的带权路径长度之和。

有了如上的概念，对于Huffman树，其定义为：

给定$n$权值作为$n$个叶子节点，构造一棵二叉树，若这棵二叉树的带权路径长度达到最小，则称这样的二叉树为最优二叉树，也称为Huffman树。

由以上的定义可以知道，Huffman树是带权路径长度最小的二叉树，对于上面的二叉树，其构造完成的Huffman树为：

二、Huffman树的构建

由上述的Huffman树可知：节点的权越小，其离树的根节点越远。那么应该如何构建Huffman树呢？以上述报文为例，首先需要统计出每个字符出现的次数作为节点的权:

接下来构建Huffman树：

• 重复以下的步骤：
  
  • 按照权值对每一个节点排序：D-F-T-E-R-A
  • 选择权值最小的两个节点，此处为D和F生成新的节点，节点的权重为这两个节点的权重之和，为2
• 直到只剩最后的根节点

按照上述的步骤，该报文的Huffman树的生成过程为：

对于树中节点的结构为：

#define LEN 512
struct huffman_node{
        char c;
        int weight;
        char huffman_code[LEN];
        huffman_node * left;
        huffman_node * right;
};

对于Huffman树的构建过程为：

int huffman_tree_create(huffman_node *&root, map<char, int> &word){
        char line[MAX_LINE];
        vector<huffman_node *> huffman_tree_node;

        map<char, int>::iterator it_t;
        for (it_t = word.begin(); it_t != word.end(); it_t++){
                // 为每一个节点申请空间
                huffman_node *node = (huffman_node *)malloc(sizeof(huffman_node));
                node->c = it_t->first;
                node->weight = it_t->second;
                node->left = NULL;
                node->right = NULL;
                huffman_tree_node.push_back(node);
        }


        // 开始从叶节点开始构建Huffman树
        while (huffman_tree_node.size() > 0){
                // 按照weight升序排序
                sort(huffman_tree_node.begin(), huffman_tree_node.end(), sort_by_weight);
                // 取出前两个节点
                if (huffman_tree_node.size() == 1){// 只有一个根结点
                        root = huffman_tree_node[0];
                        huffman_tree_node.erase(huffman_tree_node.begin());
                }else{
                        // 取出前两个
                        huffman_node *node_1 = huffman_tree_node[0];
                        huffman_node *node_2 = huffman_tree_node[1];
                        // 删除
                        huffman_tree_node.erase(huffman_tree_node.begin());
                        huffman_tree_node.erase(huffman_tree_node.begin());
                        // 生成新的节点
                        huffman_node *node = (huffman_node *)malloc(sizeof(huffman_node));
                        node->weight = node_1->weight + node_2->weight;
                        (node_1->weight < node_2->weight)?(node->left=node_1,node->right=node_2):(node->left=node_2,node->right=node_1);
                        huffman_tree_node.push_back(node);
                }
        }

        return 0;
}

其中，map结构的word为每一个字符出现的频率，是从文件中解析出来的，解析的代码为：

int read_file(FILE *fn, map<char, int> &word){
        if (fn == NULL) return 1;
        char line[MAX_LINE];
        while (fgets(line, 1024, fn)){
                fprintf(stderr, "%s\n", line);
                //解析，统计词频
                char *p = line;
                while (*p != '\0' && *p != '\n'){
                        map<char, int>::iterator it = word.find(*p);
                        if (it == word.end()){// 不存在，插入
                                word.insert(make_pair(*p, 1));
                        }else{
                                it->second ++;
                        }
                        p ++;
                }
        }
        return 0;
}

当构建好Huffman树后，我们分别利用先序遍历和中序遍历去遍历Huffman树，先序遍历的代码为：

void print_huffman_pre(huffman_node *node){
        if (node != NULL){
                fprintf(stderr, "%c\t%d\n", node->c, node->weight);
                print_huffman_pre(node->left);
                print_huffman_pre(node->right);
        }
}

中序遍历的代码为：

void print_huffman_in(huffman_node *node){
        if (node != NULL){
                print_huffman_in(node->left);
                fprintf(stderr, "%c\t%d\n", node->c, node->weight);
                print_huffman_in(node->right);
        }
}

得到的结构与上图中的结构一致。

三、由Huffman树生成Huffman编码

有了上述的Huffman树的结构，现在我们需要利用Huffman树对每一个字符编码，该编码又称为Huffman编码，Huffman编码是一种前缀编码，即一个字符的编码不是另一个字符编码的前缀。在这里约定：

• 将权值小的最为左节点，权值大的作为右节点
• 左孩子编码为0，右孩子编码为1

因此，上述的编码形式如下图所示：

从上图中，E节点的编码为：00，同理，D节点的编码为1001

Huffman编码的实现过程为：

int get_huffman_code(huffman_node *&node){
        if (node == NULL) return 1;
        // 利用层次遍历，构造每一个节点
        huffman_node *p = node;
        queue<huffman_node *> q;
        q.push(p);
        while(q.size() > 0){
                p = q.front();
                q.pop();
                if (p->left != NULL){
                        q.push(p->left);
                        strcpy((p->left)->huffman_code, p->huffman_code);
                        char *ptr = (p->left)->huffman_code;
                        while (*ptr != '\0'){
                                ptr ++;
                        }
                        *ptr = '0';
                }
                if (p->right != NULL){
                        q.push(p->right);
                        strcpy((p->right)->huffman_code, p->huffman_code);
                        char *ptr = (p->right)->huffman_code;
                        while (*ptr != '\0'){
                                ptr ++;
                        }
                        *ptr = '1';
                }
        }


        return 0;
}

利用上述的代码，测试的主函数为：

int main(){
        // 读文件
        FILE *fn = fopen("huffman", "r");
        huffman_node *root = NULL;
        map<char, int> word;
        read_file(fn, word);
        huffman_tree_create(root, word);
        fclose(fn);
        fprintf(stderr, "pre-order:\n");
        print_huffman_pre(root);
        fprintf(stderr, "in-order:\n");
        print_huffman_in(root);

        get_huffman_code(root);
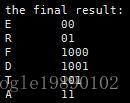
        fprintf(stderr, "the final result:\n");
        print_leaf(root);
        destory_huffman_tree(root);
        return 0;
}

print_leaf函数用于打印出每个叶节点的Huffman编码，其具体实现为：

void print_leaf(huffman_node *node){
        if (node != NULL){
                print_leaf(node->left);
                if (node->left == NULL && node->right == NULL) fprintf(stderr, "%c\t%s\n", node->c, node->huffman_code);
                print_leaf(node->right);
        }
}

destory_huffman_tree函数用于销毁Huffman树，其具体实现为：

void destory_huffman_tree(huffman_node *node){
        if (node != NULL){
                destory_huffman_tree(node->left);
                destory_huffman_tree(node->right);
                free(node);
                node = NULL;
        }
}

其最终的结果为：

参考文献

• 《大话数据结构》
• 《数据结构》(C语言版)