卷积神经网络
- 好久没写东西了,惭愧。。。。
声明:此文只是作者作为搬运工从别的博客进行复制,以变自己留做学习。如有错误恳请纠正 - 在切入卷积神经网络之前我们首先得明白这几个东西:卷积,bp神经网络,池化,卷积神经网络结构。以及最后的代码实现,和作者网上抄的几个例子。
卷积
看似比较奥秘的东西,其实就是图像矩阵与卷积核对应值相乘,然后再将其值进行求和。
3 * 3 的像素区域R与卷积核G的卷积运算:R5(中心像素)=R1G1 + R2G2 + R3G3 + R4G4 + R5G5 + R6G6 + R7G7 + R8G8 + R9G9

这得益于(卷积定理)
常用的图像模板 :


如图所示,展示了一个3×3的卷积核在5×5的图像上做卷积的过程。每个卷积都是一种特征提取方式,就像一个筛子,将图像中符合条件(激活值越大越符合条件)的部分筛选出来。

BP神经网络
BP神经网络主要由两个部分组成
- (1)工作信号正向传递子过程
- (2)误差信号反向传递子过程
BP神经网络架构

分别包含输入层,隐含层,输出层
根据经验公式隐含层节点数目为: 
其中$h$为隐含层节点数目,$m$为输入层节点数目,$n$为输出层节点数目。$a$为调节系数。
正向传递过程
设$i$,$j$两个节点的权值为$w_ij$,节点j的阈值为$b_j$,每个节点的输出值为$x_j$。
而每个节点的输出值是根据上层所有节点的输出值、当前节点与上一层所有节点的权值和当前节点的阀值还有激活函数来实现的。具体计算方法如下:

其中为激活函数,一般选取S型函数或者线性函数。
反向传递过程
在BP神经网络中,误差信号反向传递子过程比较复杂,它是基于Widrow-Hoff学习规则的。假设输出层$d_j$的所有结果为,误差函数如下:

而BP神经网络的主要目的是反复修正权值和阀值,使得误差函数值达到最小
Widrow-Hoff学习规则
是通过沿着相对误差平方和的最速下降方向,连续调整网络的权值和阀值,根据梯度下降法,权值矢量
的修正正比于当前位置上
$E(w,b)$上的梯度,对于第$j$个输出节点有
若选择激活函数

可以对激活函数进行求导

那么接下来针对$w_{ij}$

其中有

同样对修正值$b_j$进行求导

这就是著名的学习规则,通过==改变神经元之间的连接权值来减少系统实际输出和期望输出的误差==,这个规则又叫做Widrow-Hoff学习规则或者纠错学习规则。
输入层与隐含层的权值调节
假设$w_{k,j}$是输入层第k个节点和隐含层第i个节点之间的权值

其中

根据梯度下降法,那么对于隐含层和输出层之间的权值和阀值调整如下

而对于输入层和隐含层之间的权值和阀值调整同样有

池化(Pooling)
在通过卷积获得了特征 (features) 之后,下一步我们希望利用这些特征去做分类。理论上讲,人们可以用所有提取得到的特征去训练分类器,例如 softmax 分类器,但这样做面临计算量的挑战。
例如:对于一个 96X96 像素的图像,假设我们已经学习得到了400个定义在8X8输入上的特征,每一个特征和图像卷积都会得到一个 (96 − 8 + 1) * (96 − 8 + 1) = 7921 维的卷积特征,由于有 400 个特征,所以每个样例 (example) 都会得到一个 892 * 400 = 3,168,400 维的卷积特征向量。学习一个拥有超过 3 百万特征输入的分类器十分不便,并且容易出现过拟合 (over-fitting)。
为了描述大的图像,一个很自然的想法就是对不同位置的特征进行聚合统计,例如,人们可以计算图像一个区域上的某个特定特征的平均值 (或最大值)。这些概要统计特征不仅具有低得多的维度 (相比使用所有提取得到的特征),同时还会改善结果(不容易过拟合)。这种聚合的操作就叫做==池化== (pooling),有时也称==为平均池化==或者==最大池化== (取决于计算池化的方法)。

池化一般技术为
- 平均值池化
- 最大值池化
神经网络

对应的公式

单层感知机BP训练过程
- #### 感知机网络结构
- #### 前向过程
- #### 反向过程
- #### 连接权重修改过程
感知机的网络结构
感知机的网络结构只有单层的输入层和输出层。

有一个单层感知机的网络拓扑如上图所示,权重wi(i=1,2,3)被初始化为0~1之间的随机小数。
一个训练的样本我们用式子[(x1, x2),T]表示,x1,x2为输入神经元的兴奋值,T教师信号,即期望输出神经元产生的输出,T取值一般为0或者1。
(1)前向过程
利用当前的权重和输入兴奋计算Y和y的过程就是BP训练的前向过程,前向过程模拟的是脑神经的工作过程。Y和y的计算满足公式如下。

(2)错误信号反向传播过程

(单层感知机的错误信号)
Err(Y) = y * (1-y) * (T-y)
Err(y) = T-y
对于未经训练的网络,y往往和期望输出T不一样,y和T的差值构成整个神经网络的源错误信号,该信号要用来指导网络权重的修正。我们按照定义输出神经元的输入错误信号Err(Y)和输出错误信号Err(y)。
(3)连接权重的修改
方法1:
权重的修改,有两个感性直观的方法:
a.某个输出神经元的错误越大,与之相关的连接(w)就需要越多的修改;例如:Err(Y)很大,说明w修改量delta(w)也应该很大。
b.在输入神经元中,谁的兴奋值越大,对错误产生的责任就越大,其与输出神经元的连接就需要越多的修改。
例如:x1=0.1,x2=0.8。Err(Y)的出现,x2的责任更大,连接权重w2的修改量delta(w2)要比delta(w1)要更大。
基于以上两点,我们把一条连接权重的修改量定为该连接的前层神经元的输出x乘以后层神经元的Err(Y),用公式表示:

我们可以得到各权重修改量为:

算出delta(w)之后,我们通过如下公式完成对网络的更新:

==方法2==:
我们可以从多元函数求极值角度解释上述过程。模型的训练的理念是经验风险最小化,也就是要使训练数据的错误|Err(y)|最小,但是由于|Err(y)|带有绝对值的目标不方便求导,我们把模型训练目标用函数lossFun表示。lossFun定义如下公式:

对于一个样本$[(x_1,x_2),T]$,特征为$x_1$、$x_2$;类别或输出目标为T。lossFun是一个以[(x1,x2),T]为常量,以[w1,w2,w3]为变量的多元函数。模型的训练优化可看成一个多元函数求极值的问题
已知条件为:

在上面公式中,x1,x2,T为常量,w1、w2,、w3为变量。lossFun对w1求偏导得到:

同理可得:

训练样本[(x1,x2),T]时,网络参数按照梯度下降的方向求解。偏导数算出的是lossFun上升最快的方向,W的修改量delta(W)是lossFun下降最快的方向,所以delta(W)方向与梯度方向相反。

单层输出多层感知机BP训练
- 多层感知机网络结构
- 前向过程
- 反向过程
- 权值修改过程
多层感知机网络结构
在单层感知机的基础上增加若干个(本文增加一个)隐层,得到多层感知机(Multi Perceptron Machine,MLP)。结构如图所示:

图中各变量满足公式:
前向过程
反向过程
假如现在有一个样本[(x1,x2),T],用该样本训练网络时,网络优化的目标为lossFun最小。lossFun是一个关于变量w和v多元函数。网络的训练又变成多元函数求极值的问题。
求v1(隐含层->输出层)的梯度:
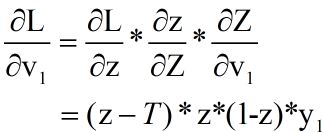
同理可以求得$v_i$的梯度
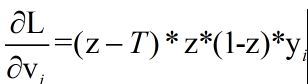
同理,可得wij(输入层->隐含层)的梯度:
权值修改
通过上述方法算得单输出多层感知机的各连接权重w和v的梯度,只要按照w和v的梯度下降方向更新网络就能完成网络训练。
多输出层多层感知机
- 网络结构
- 前向过程
- 反向过程
- 权重修改
网络结构
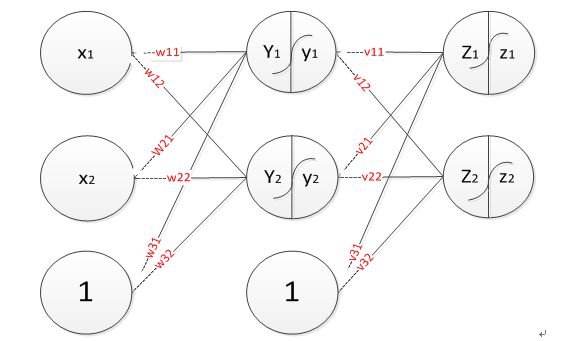
在上图的网络中,各变量满足公式:
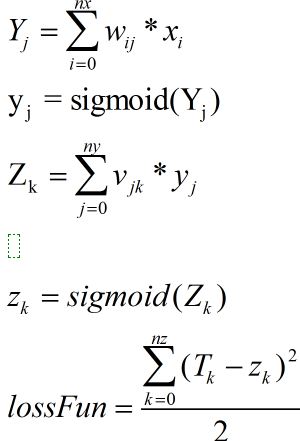
通过数学求导,得到lossFun对vjk的梯度:
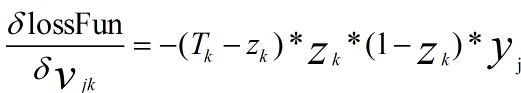
同理得到lossFun对wij的梯度:
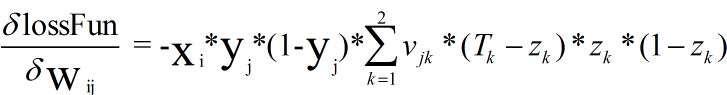
在求出权重梯度之后,只要按照梯度下降的方向更新连接权重就可以完成网络的训练。
总结
对于末层神经元,输出错误定义为:
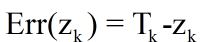
对于非末层神经元,输出错误如Err(y)由与其相连的后层神经元的输入错误Err(Z)加权求和得到,如下公式所示:
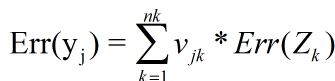
一个神经元的输入错误Err(Y)与输出错误Err(y)满足公式:
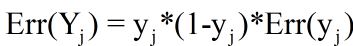
一条连接权重的更新量为该条连接前层神经元的输出乘以后层神经元的输入错误信号,如下公式所示:
卷积神经网络
- 在此节我们将步入正轨开始探索卷积神经网络,有了前面的知识应该对卷积神经网络不会那么晦涩。。。
- 卷积神经网络包含了一个由卷积层和子采样层构成的特征抽取器。在卷积神经网络的卷积层中,一个神经元只与部分邻层神经元连接
- 所谓的共享权值实则共享的是卷积核,其中卷积核可以看作一个n*n的矩阵因子。局部感知则是通过卷积核去在一张图像的像素上进行滑动卷积。多卷积核则是通过多个不同的卷积核来进行卷积。
卷积神经网络前言
在图像处理中,往往把图像表示为像素的向量,比如一个1000×1000的图像,可以表示为一个1000000的向量。在上一节中提到的神经网络中,如果隐含层数目与输入层一样,即也是1000000时,那么输入层到隐含层的参数数据为1000000×1000000=10^12,这样就太多了,基本没法训练。所以图像处理要想练成神经网络大法,必先减少参数加快速度。
卷积神经网络的几个特点:
- 局部感知
- 权值共享
- 多卷积核
上面所述只有100个参数时,表明只有1个10*10的卷积核,显然,特征提取是不充分的,我们可以添加多个卷积核,比如32个卷积核,可以学习32种特征。
卷积神经网络结构
卷积神经网络通常采用若干个卷积和子采样层的叠加结构作为特征抽取器。
卷积层与子采样层不断将特征图缩小,但是特征图的数量往往增多。特征抽取器后面接一个分类器,分类器通常由一个多层感知机构成。在特征抽取器的末尾,我们将所有的特征图展开并排列成为一个向量,称为特征向量,该特征向量作为后层分类器的输入。
卷积过程
inputx为输入原始图像(m,n),kernelW为卷积核(x,y),output Y为输出图像(m-x+1,n-y+1)。
- step1:
输入图像和filter的对应位置元素相乘再求和,最后再加上b,得到特征图。如图中所示,filter w0的第一层深度和输入图像的蓝色方框中对应元素相乘再求和得到0,其他两个深度得到2,0,则有0+2+0+1=3即图中右边特征图的第一个元素3.,卷积过后输入图像的蓝色方框再滑动.
然后经过池化层,也叫做下采样层。下采样层的作用就是减少数据量。依照上文下采样层有max pooling,ave pooling.现在我们采用的是max pooling.如下图所示:

想必大家比较感兴趣max pooling为什么不会影响整张图片。
Max pooling 还有类似 “选择句” 的功能。假如有两个节点,其中第一个节点会在某些输入情况下最大,那么网络就只在这个节点上流通信息;而另一些输入又会让第二个节点的值最大,那么网络就转而走这个节点的分支。
但是 Max pooling 也有不好的地方。因为并非所有的抓取都像上图这样的极端例子。有些周边信息对某个概念是否存在的判定也有影响。 并且 Max pooling 是对所有的 Feature Maps 进行等价的操作。就好比用相同网孔的渔网打鱼,一定会有漏网之鱼。
- step2:

然后再进行池化层采样….
- stepn:若干个卷积层和采样层。
卷积神经网络的训练过程
有了上面的知识现在到了最关键的卷积神经网络的训练过程。
与普通的BP神经网络类似主要分为三个部分:
- 前向卷积过程
- 错误反向卷积的过程
- 权值更新过程的卷积
前向卷积的过程
前向卷积过程主要为上文的卷积过程,我们知道后面有一个全连接层。其实就是一个多输入多输出的分类器。
错误反向卷积的过程
在错误信号反向传播过程中,先按照神经网络的错误反传方式得到尾部分类器中各神经元的错误信号,然后错误信号由分类器向前面的特征抽取器传播。错误信号从子采样层的特征图(subFeatureMap)往前面卷积层的特征图(featureMap)传播要通过一次full卷积过程来完成(如图3.14)。
这里的卷积和上一节卷积的略有区别。如果卷积核kernalW的长度为Mw*Mw的方阵,那么subFeatureMap的错误信号矩阵Q_err需要上下左右各拓展Mw-1行或列,与此同时卷积核自身旋转180度。subFeatureMap的错误信号矩阵P_err等于featureMap的误差矩阵Q_err卷积旋转180度的卷积核W_rot180。
更新权重的卷积过程
code:
参考:
https://wenku.baidu.com/view/4550a0b94b73f242336c5fbb.html
http://blog.csdn.net/zy3381/article/details/44409535
http://blog.csdn.net/taigw/article/details/50612963
http://blog.csdn.net/walegahaha/article/details/51945421








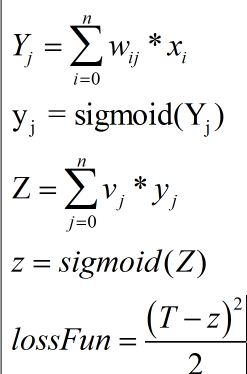
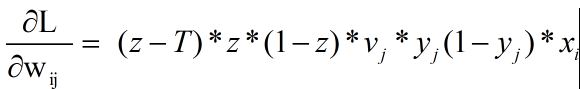
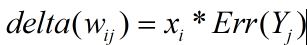














 191
191

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








