sklearn机器学习:逻辑回归LogisticRegression参数解析之梯度下降

梯度下降：重要参数max_iter

在上篇博文《sklearn机器学习:逻辑回归LogisticRegression参数解析之penalty & C》中，我们解析了参数penalty & C，本文重点讨论max_iter。
逻辑回归的目的是求解能够让模型最优化、拟合程度最好的参数ω的值，即求解能够让损失函数J(ω)最小化的ω值。
对于二元逻辑回归，有多种方法可以用来求解参数ω，最常见的有梯度下降法(Gradient Descent)，坐标下降法(Coordinate Descent)，牛顿法(Newton-Raphson method)等，其中又以梯度下降法最为著名。每种方法都涉及复杂的数学原理，但这些计算在执行的任务其实是类似的。

梯度下降求解逻辑回归

以最著名也最常用的梯度下降法为例，来看逻辑回归的参数求解过程。观察下面的图像，这个图像的横坐标是参数，纵坐标是损失函数J(ω)，最简化的情况下，只有一个特征对应只有一个参数。现在求解损失函数值最小化时的ω解，执行过程如下：

1. 首先在图像上随机投掷一个小球，让小球向着损失函数最低的点去滚动
2. 由于没有重力，所以需要告诉小球三件事，才能够让小球滚动起来：
   (1) 滚动的方向：必须是损失函数的值下降最快的方向
   (2) 每次滚动的距离
   (3) 要滚动的次数
   
   然而真正的损失函数可能会长这样：
   
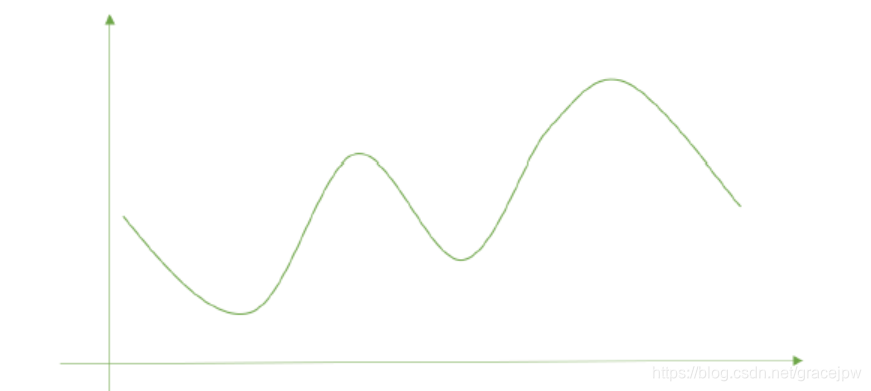
   现在有一个带两个特征并且没有截距的逻辑回归y(x₁,x₂)，两个特征所对应的参数分别为(ω₁,ω₂)。下面这个华丽的平面就是损失函数J(ω₁,ω₂)在以ω₁、ω₂和J为坐标轴的三维立体坐标系上的图像。现在，寻求的是损失函数的最小值，也就是图像的最低点。
   
   在这个图像上随机放一个小球，松手，这个小球就会顺着这个华丽的平面滚落，直到滚到深蓝色的区域——损失函数的最低点。同样，为了严格监控这个小球的行为，让小球每次滚动的距离有限，不让他一次性滚到最低点，并且最多只允许它滚动100步，还要记下它每次滚动的方向，直到它滚到图像上的最低点。
   可以看到，小球高处滑落，在深蓝色的区域中来回震荡，最终停留在了图像凹陷处的某个点上。可以观察到几个现象：
   首先，小球并不是一开始就直向着最低点去的，它先一口气冲到了蓝色区域边缘，后来又折回来，已经规定了小球是多次滚动，所以可见，小球每次滚动的方向都是不同的。
   另外，小球在进入深蓝色区域后，并没有直接找到某个点，而是在深蓝色区域中来回震荡了了数次才停下。这有两种可能：1) 小球已经滚到了了图像的最低点，所以停下了，2) 由于设定的步数限制，小球还没有找到最低点，但也只好在100步的时候停下了。也就是说，小球不一定滚到了图像的最低处。
   但无论如何，小球停下的是我们在现有状况下可以获得的唯一点。如果够幸运，这个点就是图像的最低点，那只要找到这个点的对应坐标( ${\omega }_1^{\ast },{\omega }_2^{\ast },J_{min}$)，就可以获取能够让损失函数最小的参数取值$[{\omega }_1^{\ast },{\omega }_2^{\ast }]$。如此，梯度下降的过程就已经完成。
   在此过程中，小球其实就是一组组的坐标点（ω₁,ω₂,J）；小球每次滚动的方向就是那一个坐标点的梯度向量方向，因为每滚动一步，小球所在的位置都发生变化，坐标点和坐标点对应的梯度向量都发生变化，所以每次滚动的方向也都不一样；人为设置的100次滚动限制，就是sklearn中逻辑回归的参数max_iter，代表着能走的最大步数，即最大迭代次数。每次滚动的距离限制，由“步长“决定，在sklearn中是被提前定义好的，人为不可控。
   所以梯度下降，其实就是在众多可能的值中遍历，一次次求解坐标点的梯度向量，不断让损失函数的取值逐渐逼近最小值，再返回这个最小值对应的参数取值$[{\omega }_1^{\ast },{\omega }_2^{\ast }]$的过程。

梯度下降

在多元函数上对各个自变量量求∂偏导数，把求得的各个自变量量的偏导数以向量的形式写出来，就是梯度。比如损失函数J(ω₁,ω₂)，其自变量是逻辑回归预测函数y_ω(x)的参数ω₁,ω₂，在损失函数上对ω₁,ω₂求偏导数，求得的梯度向量d就是 [ ∂ J ∂ ω 1 , ∂