传送门:E. ZS and The Birthday Paradox
描述:
题意:
有2^n天,k个人,求至少2个人生日相同的概率,要求分子分母约分后再对1e6+3取模。
思路:
正难则反,我们就该从反面考虑考虑
"任意两个人的生日都不在同一天"的情况数相当于从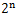
当k>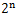
那么剩下的情况,即k≤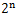
∴"至少有两个人的生日在同一天的概率"=
下面我们来计算这一部分:
因为分母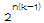
那接下来,问题的关键就是求分子式中有多少个2
对于分子中第i项分子式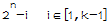
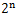
例如i=4时,该项分子式有2个2;i=16时,该项分子式有4个2
那最终把每项分子式中2的个数加起来便是tmp值,故约分之后,结果为
因为结果需要取模,于是便涉及到了除法取模,然后理所应当的就需要用到乘法逆元
那么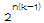
这时候就需要想到费马小定理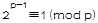
逆元部分也是如此,可以通过费马小定理降幂之后再求解
那分子部分呢?
观察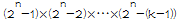
那么当k-1≥mod时,k-1个连续整数中必有一个能被mod整除,这就意味着取模之后结果为0,那k-1个连续整数的乘积就是0
而当k-1<mod时,因为mod的值不大,所以我们可以暴力循环求出分子
代码:
#include <bits/stdc++.h>
#define ll __int64
using namespace std;
template<class T> void read(T&num) {
char CH; bool F=false;
for(CH=getchar();CH<'0'||CH>'9';F= CH=='-',CH=getchar());
for(num=0;CH>='0'&&CH<='9';num=num*10+CH-'0',CH=getchar());
F && (num=-num);
}
const ll mod=1e6+3;
ll pow_mod(ll x, ll n){
ll res=1;
while(n>0){
if(n&1)res=res*x%mod;
x=x*x%mod;
n>>=1;
}
return res;
}
bool ok(ll n, ll k){
ll s=1;
for(int i=1; i<=n ;i++){
s*=2;
if(s>=k)return false;
}
return true;
}
int main(){
ll n,k;
read(n);read(k);
if(ok(n,k)){
puts("1 1");
return 0;
}
ll A,B,GCD,tmp,i;
B=pow_mod(2, n%(mod-1)*( (k%(mod-1)-1+(mod-1))%(mod-1) )%(mod-1) );
for(tmp=0,i=2; i<=k-1; i*=2)tmp+=(k-1)/i;
GCD=pow_mod(2, tmp%(mod-1)*(mod-2)%(mod-1));
B=B*GCD%mod;
if(k-1>=mod)printf("%I64d %I64d\n",B,B);
else{
A=1;
for(i=1; i<=k-1; i++)
A=A*(( pow_mod(2,n%(mod-1)) -i+mod)%mod) %mod;
A=A*GCD%mod;
printf("%I64d %I64d\n",(B-A+mod)%mod,B);
}
return 0;
}










 . He wants to find the values of
. He wants to find the values of  ), print the
), print the  , so
, so 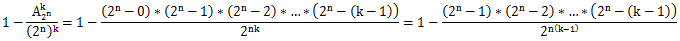
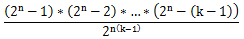
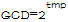
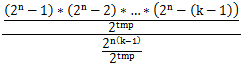
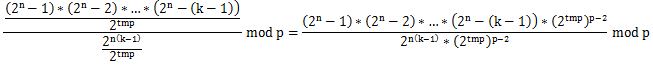














 207
207











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








