Xgboost原理及使用

---

集成学习

集成学习（ensemble learning）通过构建并结合多个学习器来完成学习任务，有时也被称为多分类器系统（multi-classifier system）、基于委员会的学习（committee-based learning）等。如下图所示，集成学习的一般构造：先产生一组“个体学习器”（individual learner），再用某种策略将它们结合起来。

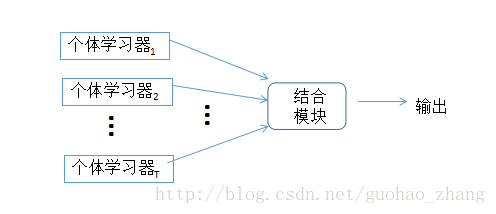
个体学习器通常由一个现有的学习算法从训练数据中产生。例如C4.5决策树算法、BP神经网络算法等，此时集成中只包含同种类型的个体学习器，例如“决策树集成”中全是决策树，“神经网络集成”中全是神经网络，这样的集成是“同质”的（homogeneous）。同质集成中的个体学习器亦称为“基学习器”（base learner），相应的学习算法称为“基学习算法”（base learning algorithm）。集成也可包含不同类型的个体学习器，例如同时包含决策树和神经网络，这样的集成是“异质”的（heterogeneous）。
异质集成中的个体学习器由不同的学习算法生成，这时就不再有基学习算法；相应的，个体学习器一般不称为基学习器，常称为“组件学习器”（component learner）或直接称为个体学习器。
常见的集成学习方法有：袋装组合法（Bagging）、自适应提升（AdaBoost）、随机森林（Random Forest）和旋转森林（Rotation Forest）等。

【详情解释请参考 《机器学习》 周志华 清华大学出版社】

监督学习

监督学习是从标记的训练数据来推断一个功能的机器学习任务。训练数据包括一套训练示例。在监督学习中，每个实例都是由一个输入对象（通常为矢量）和一个期望的输出值（也称为监督信号）组成。监督学习算法是分析该训练数据，并产生一个推断的功能，其可以用于映射出新的实例。

有监督学习大致可以粗略分为模型、参数、目标函数三部分。

Model：how to make prediction Yi given Xi ，常见模型如：线性模型（include 线性回归、逻辑回归）

参数：需要从数据中学习的东西。

目标函数：按照我的理解，每一个算法都有一个目标函数（objective function），算法就是让这个目标函数达到最优。

关于目标函数的详细说明，我看过一篇知乎上的讨论，解释得挺详细。
机器学习中的目标函数、损失函数、代价函数有什么区别？

在这里，目标函数=训练误差项+正则项

树模型

回归树（ Regression Tree CART），像决策树一样，有着决策条件，而且Regression Tree的每个叶子节点都有一个分数（Score）。

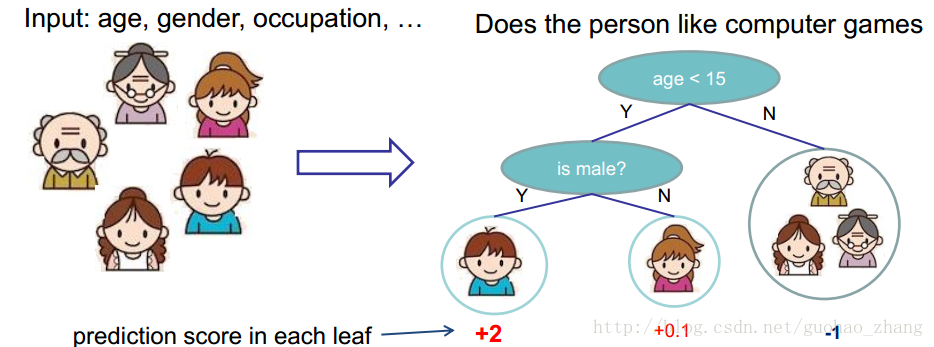
关于回归树的概概念，之前一直留着两张图，可以快速理解一下回归树是什么。

在这里得提到一下，
ID3算法采用信息增益，C4.5算法采用信息增益比，CART采用Gini系数。
它们结构是差不多的，唯一不同的就是目标函数的构建不一样。

树模型的组合集成（ensemble）

单棵树过于简单而无法有效预测，所以需要更强力的模型：树的集成。

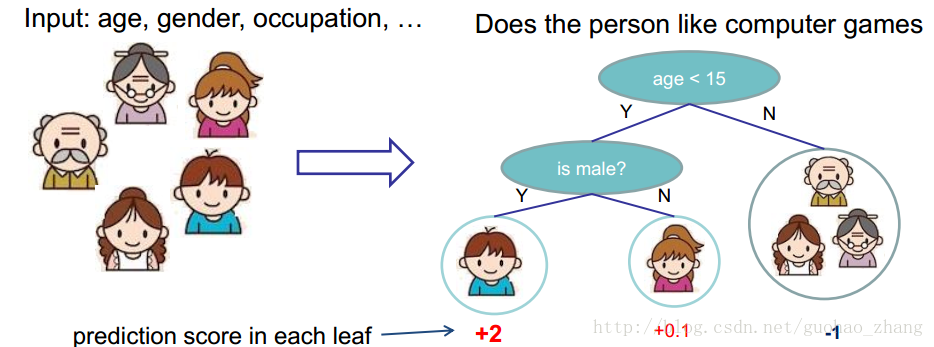
假设我们有K trees，

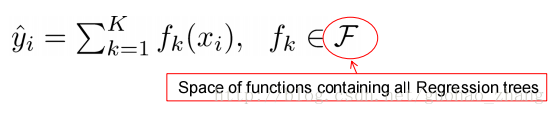
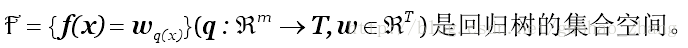
q表示每棵树的结构映射到样本所对应的叶子的索引。T指的是树的叶子数量。每个fk对应于一个独立树结构q和叶子权重w。

目标函数是，

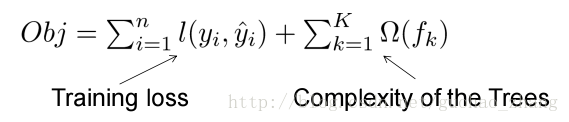
其中，Complexity of the Trees 后面再来，先进行提升树。

梯度树提升（Gradient Tree Boosting）

因为它们都是树而不是数字向量，我们没办法使用像SGD等方法去找到f。所以使用Additive Training的方式
Tree learning，Additive Training (Boosting)
Start from constant prediction, add a new function each time.

第t轮预测是：

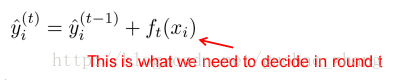
第i个样本在第t轮的模型预测值，保留t-1轮的模型预测值后，加入一个新的函数。选择在每一轮加入新函数是为了尽可能的让目标函数最大程度的降低。于是，改写目标函数为：

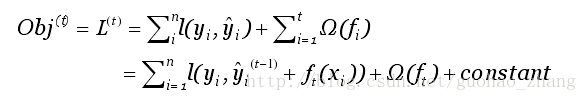
找到 ft 来优化这个目标函数。当误差函数L是平方误差的情况下，目标函数可以写成：

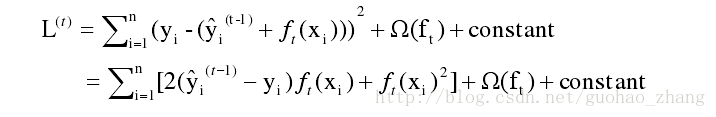
采用泰勒展开来近似定义目标函数，方便进一步的计算。

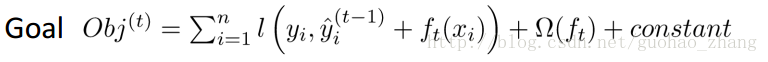
用泰勒二阶展开来近似原来的目标后：
泰勒展开公式:

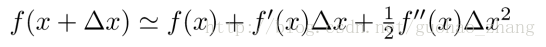
定义：

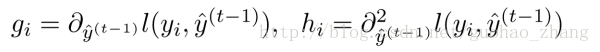
展开：

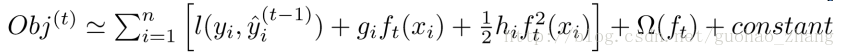
把常数项移除后，获得了相对统一的目标函数。只依赖每个数据点在误差函数上的一阶和二阶导是这个目标函数的明显特点。

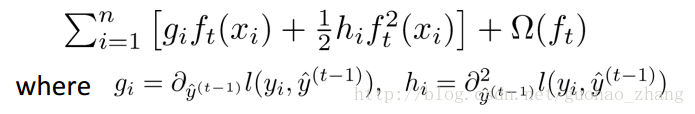
这样的形式包含所有可求导的目标函数。也就是说，用于实现的代码可求解包括回归、分类和排序的各种问题。

上面还没说到的树的复杂度

上述公式中，

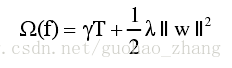
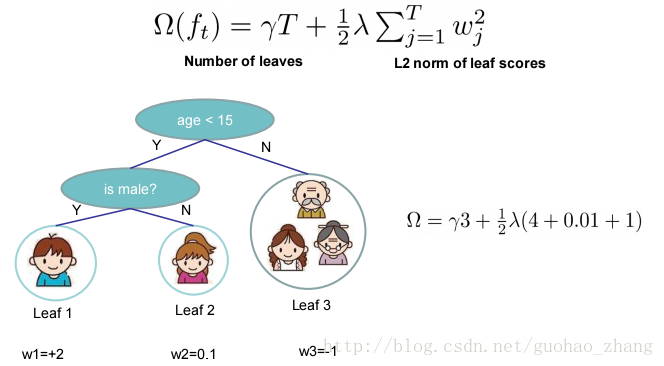
用来定义树的复杂度。每棵树分成结构部分q和叶子权重部分w。复杂度包括：每棵树中的节点个数，及每棵树中叶子节点上的权重的L2模平方。虽然定义方式不唯一，但是这种定义下学习出的树的效果较好。

用这种新的定义将目标函数进行改写：

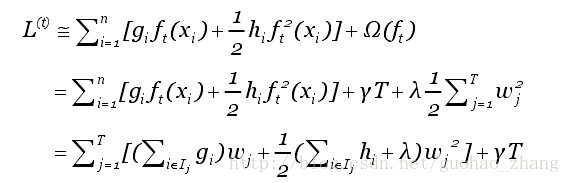
再定义 Gi Hi

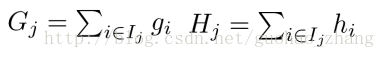
则目标函数为

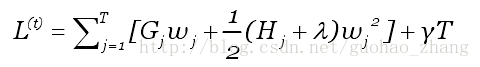
假设树的结构q(x)已知，通过目标函数计算叶子j最优的权重值：

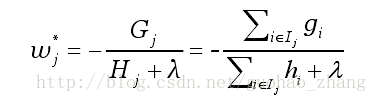
以及计算对应的最优目标函数值：

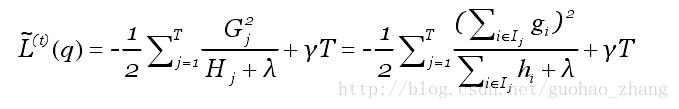
上述公式可以被作为一个对于树结构q进行打分的函数，类似gini系数。可以把它叫做结构分数(structure score)，这个分数越小树结构越好。
算法重复地利用打分函数不断枚举不同的树结构来寻找一个最优结构的树，加入到模型中。
一般情况下，无法枚举所有的树结构q，所以采用贪心算法从一个单叶子节点开始迭代来给树添加分支这种方法进行代替。

最后使用原作者的对此算法的总结就是：

【未完待续……】