（五）Singer模型和“当前”统计模型讲解及仿真

滤波~

已于 2023-12-25 22:04:17 修改

阅读量2.6k

点赞数 56

分类专栏：滤波算法仿真与实践文章标签： matlab 算法

于 2023-12-25 22:03:23 首次发布

本文链接：https://blog.csdn.net/h320130/article/details/135196189

版权

滤波算法仿真与实践专栏收录该内容

8 篇文章 13 订阅

订阅专栏

前言

Singer模型和“当前”统计模型是描述目标机动运动的两种经典模型。首先本博客针对机动目标跟踪的基本框架进行了介绍；同时，针对Singer模型和“当前”统计模型的物理含义进行了解释，并进行了详细的公式推导；最后利用卡尔曼滤波（KF）对“当前”统计模型进行滤波，验证了所提算法的有效性。

一、基础知识

（一）机动目标跟踪框架

1.单目标跟踪

单目标跟踪基本要素包括量测数据形成、目标机动模型和自适应滤波和预测以及跟踪坐标系和滤波状态的选取。单机动目标跟踪本质上就是一个递推滤波过程。首先，由传感器获得目标的量测数据，通过量测模型获得量测数据与目标位置的关系函数将此与目标的当前状态一起作为输入，由跟踪滤波器结合机动目标模型得到当前目标状态的估计值和预测值，并把得到的状态作为下一时刻的初始状态，从而完成单机动目标跟踪过程。基本框图如下：

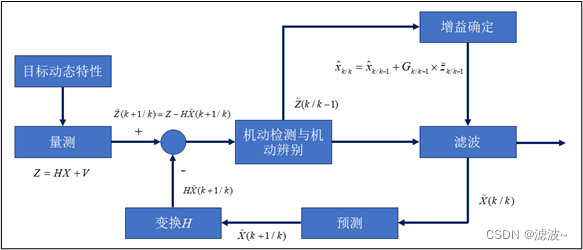
图中目标的动态向量包含位置速度和加速的状态向量 $X$ 表示，量测用 $Z$ 表示，新息向量用 $\tilde{z}_{k\mid k-1}$ 表示。首先由量测Z和状态预测计算残差 $\tilde{z}_{k\mid k-1}$ ；然后根据 $\tilde{z}_{k\mid k-1}$ 的变化进行机动检测或者机动辨别；其次按照某一准则或逻辑调整滤波增益与协方差矩阵或者实时辨识出目标机动特性；最后由滤波算法得到目标的估计值和预测值，从而完成目标跟踪功能。

2.多目标跟踪

相比与单目标跟踪，多目标跟踪基本要素不仅包括单机动目标的基本要素，还形成了一些新的要素，主要包括跟踪门规则，数据关联和跟踪维持等。其中数据关联是多机动目标跟踪的核心。基本框图如下：

（二）Singer模型

Singer模型假定目标的机动加速度 $a(t)$ 是一个零均值、平稳的一阶马尔可夫过程，且其自相关函数为：

${R_a}(\tau ) = {\rm{E[}}a(t + \tau )a(t)] = \sigma _m^2{e^{ - a\left| \tau \right|}}$

其中， $a$ 是机动频率，定义为机动时间常数的倒数，通常取经验值； $\sigma _m^2$ 是加速度方差。

当机动加速度 $a(t)$ 通过“白化”处理后，它可用输入为白噪声的一阶时间相关模型来表示，式(2)即：

$\dot a(t) = - \alpha a(t) + \tilde v(t)$

其中， $\dot a(t)$ 为机动加速度 $a(t)$ 的导数； $\tilde v(t)$ 表示均值为0、方差为 $2\alpha \sigma _m^2$ 的高斯白噪声。

假设系统的状态向量为 $X = {[x,\dot x,\ddot x]^{\rm T}}$ ， $x,\dot x,\ddot x$ 分别为目标在x轴上的距离、速度和机动加速度。由式(2)可得连续时间系统中的Singer模型为：

$\begin{bmatrix} {\dot x} \\ {\ddot x} \\ {\dot a} \end{bmatrix}= \begin{bmatrix}0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & -\alpha \end{bmatrix} \begin{bmatrix}x \\ {\dot x} \\ {\ddot x} \end{bmatrix} + \begin{bmatrix}0 \\0 \\ {\tilde v} \end{bmatrix}$

对于采样间隔T,根据连续时间系统与离散时间系统的关系可得到对应的离散状态方程如下：

$X(k + 1) = F(k)X(k) + V(k)$

状态转移矩阵为：

$F(k) =\begin{bmatrix}1 & T & {(\alpha T - 1 + {e^{ - \alpha T}})/{\alpha ^2}} \\ 0 & 1 & {(1 - {e^{ - \alpha T}})/\alpha } \\ 0 & 0 & {{e^{ - \alpha T}}} \\ \end{bmatrix}$

过程噪声矩阵：

$Q(k) = 2\alpha \sigma _m^2 \begin{bmatrix} {{q_{11}}} & {{q_{12}}} & {{q_{13}}} \\ {{q_{21}}} & {{q_{22}}} & {{q_{23}}} \\ {{q_{31}}} & {{q_{32}}} & {{q_{33}}} \end {bmatrix}$

其中， ${q_{ij}}(i = 1,2,3;j = 1,2,3)$ 为 $\alpha$ 和 $T$ 的函数，具体为：

$\begin{cases} & {q_{11}} = (1 - {e^{ - 2\alpha T}} + 2\alpha T + {{2{\alpha ^3}} \over 3} - 2{\alpha ^2}{T^2} - 4\alpha T{e^{ - \alpha T}}) \\ & {q_{12}} = {1 \over {2{\alpha ^4}}}({e^{ - 2\alpha T}} + 1 - 2{e^{ - \alpha T}} + 2\alpha T{e^{ - \alpha T}} - 2\alpha T + {\alpha ^2}{T^2}) \\ & {q_{13}} = {1 \over {2{\alpha ^3}}}(1 - {e^{ - 2\alpha T}} - 2\alpha T{e^{ - \alpha T}}) \\ & {q_{22}} = {1 \over {2{\alpha ^3}}}(4{e^{ - \alpha T}} - 3 - {e^{ - 2\alpha T}} + 2\alpha T) \\ & {q_{23}} = {1 \over {2{\alpha ^2}}}({e^{ - 2\alpha T}} + 1 - 2{e^{ - \alpha T}}) \\ & {q_{33}} = {1 \over {2\alpha }}(1 - {e^{ - 2\alpha T}}) \end{cases}$

（三）“当前”统计模型

“当前”统计模型本质上是一个具有自适应非零均值机动加速度的Singer模型。假设目标在当前时刻以某一机动加速度运动，则下一时刻目标机动加速度的取值范围是有限的，而且总是在当前时刻机动加速度的某一邻域内。实际情况中，目标在当前时刻的机动加速度越大，下一时刻目标的机动加速度出现大幅度偏离的概率越小。“当前”统计模型算法正是以此为出发点，用修正的瑞利分布描述目标未知机动加速度的概率分布，将目标的随机机动当作一个修正的瑞利-马尔可夫过程进行处理。

假设目标状态方程为： $X(k + 1) = F(k)X(k) + G(k)\bar a + V(k)$

其中， $X(k)$ 、 $F(k)$ 与Singer模型中的相同， $G(k)$ 称为输入控制矩阵，即：

$G(k) = \begin{bmatrix} {{1 \over \alpha }( - T + {{\alpha {T^2}} \over 2} + {{1 - {e^{ - \alpha T}}} \over \alpha })} \\ {T - {{1 - {e^{ - \alpha T}}} \over \alpha }} \\ {1 - {e^{ - \alpha T}}} \end{bmatrix}$

过程噪声矩阵：

$Q(k) = {\rm{E}}(V(k)V'(k)) = 2\alpha \sigma _a^2\begin{bmatrix} {{q_{11}}} & {{q_{12}}} & {{q_{13}}} \\ {{q_{21}}} & {{q_{22}}} & {{q_{23}}} \\ {{q_{13}}} & {{q_{23}}} & {{q_{33}}} \end{bmatrix}$

其中，具体的表达式见上述Singer模型， $\alpha$ 为自相关时间常数，而 $\sigma _a^2$ 为机动加速度方差， $\bar a(k)$ 为机动加速度均值，即：

$\sigma _a^2 = {{4 - \pi } \over \pi }\left[ {{a_{\max }} - \bar a(k)} \right]$

$\bar a(k) = \hat {\ddot x}(k/k - 1)$

进一步预测方程为：

$\hat X(k/k - 1) = F(k)\hat X(k - 1/k - 1) + G(k)\bar a(k)$

当前统计模型算法已经具备了根据前一时刻的加速度估值来自自适应地调整过程噪声的能力，其更关心的是目标机动的当前统计特征，即当目标以某一加速度机动时，起下一时刻的加速度变化范围是有限的，只能在当前加速度的某一邻域内，因而与Singer模型算法相比，当前统计模型算法更能真实地反映目标机动范围和强度的变化。

二、仿真验证

（一）仿真设置

T=1;% 观测周期

obs = 50; % 观测点数

aMax = 9; %最大加速度

aMin = -5; %最小加速度

alpha = 1/20; %机动频率

sigma=0.1 ; %机动加速度初始方差

sigma2=40; %测量噪声标准差

sig3= sigma2^2; % 测量值方差

目标运动模型采用“当前”统计模型，滤波方式采用卡尔曼滤波，对应代码如下：

% kalman滤波
for n=4 : obs-1

    X1 = A * Xk(:,n) + U*[Xk(3,n);Xk(6,n)] ;    %% 预测
    %卡尔曼滤波器递推方程
    if(Xk(3,n)>0)
      sigma=((4-pi)*(aMax-Xk(3,n))^2)/pi;         
    else
      sigma=((4-pi)*(aMin+Xk(3,n))^2)/pi;            
    end   
    P1 = A * P_EKF * A'+ Q *sigma;    %预测误差  

    T=inv(H * P1 * H' + R);
    K = P1 * H'*T;      %增益
    P_EKF = (eye(size(K * H)) - K * H) * P1;  %滤波误差协方差
    Xk(:,n+1) = X1 + K * (Y3(:,n+1) - H*X1); 
    %Y(:,n+1)是n+1时刻观测值 X1是n+1时刻预测值  X(:,n+1)是n+1时刻滤波值  
end

（二）仿真结果

绘图部分代码如下：

MEAN_EKF_ERRX = mean(ex);                 %求X轴上的EKF误差均值
VAR_EKF_ERRX = var(ey);                   %求y轴上的EKF误差方差
up = 1:obs;
figure(1);
plot(M(1, up),M(2, up),'r:*');
grid on
hold on
plot(Xk(1, up),Xk(4, up), 'g-o');
hold on
plot(Y3(1, up),Y3(2, up), 'b-^');
title('KF定位滤波图');
xlabel('x坐标/m'),ylabel('y坐标/m'),
legend('真实轨迹','KF定位滤波结果','量测定位轨迹');

figure(2)
plot(M(1,up),ex(1,up),'r-*');
hold on
plot(M(1,up),ex1(1,up),'b-^');
grid on
xlabel('x坐标/m'),ylabel('X方向误差/m'),
title('KF定位误差图'),
legend('KF','量测');

figure(3)
plot(M(1,up),ey(1,up),'r-*');
hold on
plot(M(1,up),ey1(1,up),'b-^');
grid on
xlabel('y坐标/m'),ylabel('Y方向误差/m'),
title('KF定位误差图'),
legend('KF','量测');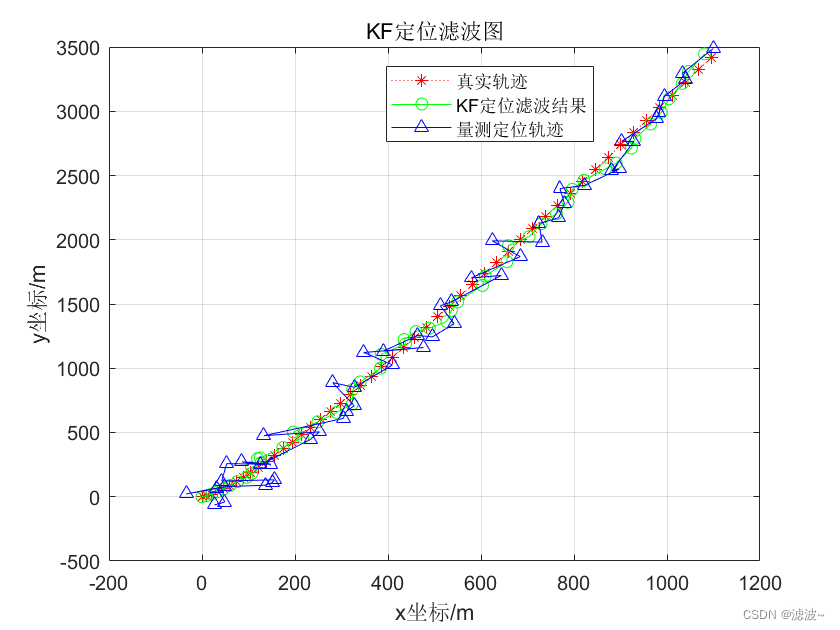

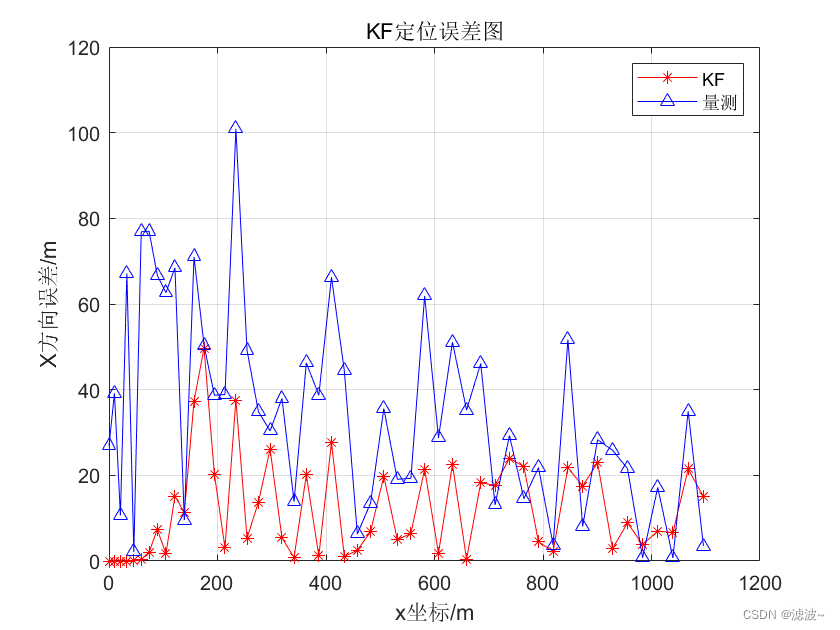
从第一张图中可以看出，程序能对目标进行有效的跟踪。定位滤波后的轨迹与真实值之间的误差明显小于量测定位轨迹与真实值之间的误差。说明滤波有效地提升了目标的定位精度，减少了噪声对于目标定位的影响。从第二张图和第三张图中可以看出，X轴和Y轴方向的量测定位误差明显大于目标的滤波定位误差，说明滤波后的定位精度明显提升，滤波是有效的。

总结

以上就是今天要讲的内容，本文简单介绍了两种目标运动模型，即Singer模型和和“当前”统计模型，并对针对当前统计模型进行了卡尔曼滤波，Singer模型对应的卡尔曼滤波程序可在对应的资源中下载。希望今天的分享能帮助到大家，之后会分享更多优质内容。

滤波~

关注

56
点赞
踩
44

收藏

觉得还不错? 一键收藏
0
评论
（五）Singer模型和“当前”统计模型讲解及仿真

Singer模型和“当前”统计模型是描述目标机动运动的两种经典模型。首先本博客针对机动目标跟踪的基本框架进行了介绍；同时，针对Singer模型和“当前”统计模型的物理含义进行了解释，并进行了详细的公式推导；最后利用卡尔曼滤波（KF）对“当前”统计模型进行滤波，验证了所提算法的有效性。
复制链接

扫一扫