#有时间要弄懂的详细过程:
http://m.blog.csdn.net/article/details?id=52290361
#待做题:
http://blog.csdn.net/acdreamers/article/details/8050018
模板:
#include<stdio.h>
#include<iostream>
using namespace std;
typedef long long ll;
int a[4],m[4];
void exgcd(int a,int b,int& x,int& y)
{
if(b == 0)
{
x = 1;
y = 0;
return; //表示程序退出,但是没有返回值
}
exgcd(b,a%b,x,y);
int temp = x;
x = y;
y = temp - (a/b) * y;
}
int CRT(int a[],int m[],int k)//a[]为余数,b[]为除数,k为给定一次线性同余式的个数即系数对的个数
{
int mm=1;//mm为余数的公倍数
int result=0;
for(int i=0;i<k;i++)
mm*=m[i];
for(int i=0;i<k;i++)
{
int x,y;
int mi=mm/m[i];
exgcd(mi,m[i],x,y);//求逆元x
result=(result+ mi*x*a[i])%mm;
}
return (result%mm+mm)%mm;//落在(0, mm)之间,防止result为负数
/*
即:
if(result<0)
return result+mm;
return result;
*/
}
Chinese remainder theorem(CRT):
中国剩余定理是求解一次线性同余方程组的方法。
中国剩余定理:
假设整数m1,m2, … ,mn两两互素,则同余方程组
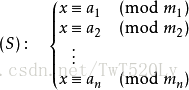
有整数解。
设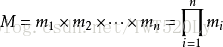
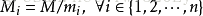
设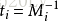
那么在模M下的解是唯一的。
应用举例:
- //一个数被3除余1,被4除余2,被5除余4,这个数最小是几?
- //题中3、4、5三个数两两互质。
- //则〔4,5〕=20;〔3,5〕=15;〔3,4〕=12;〔3,4,5〕=60。
- //为了使20被3除余1,用20×2=40;
- //使15被4除余1,用15×3=45;
- //使12被5除余1,用12×3=36。
- //然后,40×1+45×2+36×4=274,
- //因为,274>60,所以,274%60=34,就是所求的数。
-
•以「韩信点兵」为例,假设x是那个未知数,而除3,5,7后的余数分别为r1,r2,r3。因此有
x≡r1(mod 3)
x≡r2(mod 5)
x≡r3(mod 7)
解:(15*?)%7=1
(35*??)%3=1
(21*???)%5=1
X=(?*7+??*3+???*5)%(3*5*7)
方法一:套模板
#include<stdio.h>
#include<iostream>
using namespace std;
typedef long long ll;
int a[4],m[4];
void exgcd(int a,int b,int& x,int& y)
{
if(b == 0)
{
x = 1;
y = 0;
return; //表示程序退出,但是没有返回值
}
exgcd(b,a%b,x,y);
int temp = x;
x = y;
y = temp - (a/b) * y;
}
int CRT(int a[],int m[],int k)//a[]为余数,b[]为除数,k为给定一次线性同余式的个数即系数对的个数
{
int mm=1;//mm为余数的公倍数
int result=0;
for(int i=0;i<k;i++)
mm*=m[i];
for(int i=0;i<k;i++)
{
int x,y;
int mi=mm/m[i];
exgcd(mi,m[i],x,y);//求逆元x
result=(result+ mi*x*a[i])%mm;
}
return (result%mm+mm)%mm;//落在(0, mm)之间,防止result为负数
/*
即:
if(result<0)
return result+mm;
return result;
*/
}
int main()
{
int p, e, i, d, t = 1;
while(cin>>p>>e>>i>>d)
{
if(p == -1 && e == -1 && i == -1 && d == -1)
break;
while(p>23)
p-=23;
while(e>28)
e-=28;
while(i>33)
i-=33;
a[0] = p;
a[1] = e;
a[2] = i;
m[0] = 23;
m[1] = 28;
m[2] = 33;
int ans = CRT(a, m, 3);
if(ans <= d)
ans += 21252;
cout<<"Case "<<t++<<": the next triple peak occurs in "<<ans - d<<" days."<<endl;
}
return 0;
}方法二:数学方法
#include<iostream>
using namespace std;
int main(void)
{
int p,e,i,d;
int time=1;
while(cin>>p>>e>>i>>d)
{
if(p==-1 && e==-1 && i==-1 && d==-1)
break;
int lcm=21252; // lcm(23,28,33)
int n=(5544*p+14421*e+1288*i-d+21252)%21252;
if(n==0)
n=21252;
cout<<"Case "<<time++<<": the next triple peak occurs in "<<n<<" days."<<endl;
}
return 0;
} 









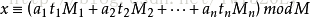














 2959
2959

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








