leetcode:Longest Palindromic Substring

    这道题目真是弄了很久啊，然后查了好多相关知识，哎，最近貌似一直很焦躁，我这是怎么了，不能继续这么下去啊，加油！

    英文原文地址：http://leetcode.com/2011/11/longest-palindromic-substring-part-i.html

1.回文简介

      首先，介绍下回文的含义。回文就是对称的序列，无论从前往后读，还是从后往前读，都是一样的。例如，“aba”是回文，而"abc"不是回文。

2.很容易犯的一个错误：

    很多人都会快速提出这么一个有漏洞的解决方案： 逆转字符串序列S为S'，然后寻找S和S'的最长公共子串（longest common substring），即最长相同回文子串。

    这看起来是正确的，但是却存在漏洞。让我们来用几个例子验证下，S="caba",S'="abac" ，其最长公共子串为"aba"，答案正确。让我们试下另外一个例子，S = “abacdfgdcaba”, S’ = “abacdgfdcaba”，其最长公共子串为“abacd”。显然，这不是一个回文。我们可以看到，这个方法的问题出在存在非回文的公共子串。正确的方法是，当找到一个最长公共子串时，检查其索引值是否正确，如果正确，就将其设置为最长回文子串，否则就跳过，寻找下一个最长回文子串。

     显然，这个算法是动态规划的思想，空间复杂度和时间复杂度都是O(n^2)。

3.暴力解法

    暴力解法需要检查所有的子串（任意的开始位置和结束位置）是否为回文。首先，一个长度为n的字符串存在n^2个子串，另外，检查一个字符串是不是回文需要O(n)的时间，所以其时间复杂度为O(n^3)。

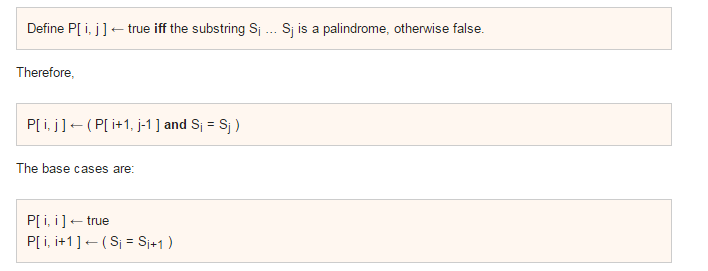
4.动态规划算法

    首先，我们应该避免无效计算。例如，"ababa"。如果我们早就知道"bab"是回文，显然“ababa”就是回文（因为“bab”两侧的字符对称相等）。更公式化的陈述为：

    代码为：

public class Solution {
    public String longestPalindrome(String s) {
        
    	 int n = s.length();
    	  int longestBegin = 0;
    	  int maxLen = 1;
    	  boolean table[][] = new boolean[1000][1000];
    	  for (int i = 0; i < n; i++) {
    	    table[i][i] = true;
    	  }
    	  for (int i = 0; i < n-1; i++) {
    	    if (s.charAt(i) == s.charAt(i+1)) {
    	      table[i][i+1] = true;
    	      longestBegin = i;
    	      maxLen = 2;
    	    }
    	  }
    	  for (int len = 3; len <= n; len++) {
    	    for (int i = 0; i < n-len+1; i++) {
    	      int j = i+len-1;
    	      if (s.charAt(i) == s.charAt(j) && table[i+1][j-1]) {
    	        table[i][j] = true;
    	        longestBegin = i;
    	        maxLen = len;
    	      }
    	    }
    	  }
    	  return s.substring(longestBegin, longestBegin+maxLen);
     
    }
}

5.简单方法，时间复杂度为O(n^2)，空间复杂度O(1)

    通过观察可知，回文以中心位置左右对称。因此，回文可以从中心开始拓展而成。一个长度为n的序列，存在2n-1个这样的中心。为什么是2n-1个中心，而不是n个中心呢？原因是中心可能存在于两个字符之间（长度为偶数的回文，例如"abba"，它的中心就位于两个'b'之间）。又因为扩展一个回文需要花费O(n)的时间，所以整个的时间复杂度为O(n^2)。代码如下：

public class Solution {
    public String expandAroundCenter(String s, int c1, int c2) {
    	  int l = c1, r = c2;
    	  int n = s.length();
    	  while (l >= 0 && r <= n-1 && s.charAt(l) == s.charAt(r)) {
    	    l--;
    	    r++;
    	  }
    	  return s.substring(l+1, r);
     }
    	 
     public String longestPalindrome(String s)  {
    	  int n = s.length();
    	  if (n == 0) return "";
    	  String longest = s.substring(0, 1);  // a single char itself is a palindrome
    	  for (int i = 0; i < n-1; i++) {
    	    String p1 = expandAroundCenter(s, i, i);
    	    if (p1.length() > longest.length())
    	      longest = p1;
    	 
    	    String p2 = expandAroundCenter(s, i, i+1);
    	    if (p2.length() > longest.length())
    	      longest = p2;
    	  }
    	  return longest;
    }
}

    想想如何简化算法的复杂度。考虑最坏的情况，即输入字符串包含多个回文，且回文之间存在覆盖现象。例如，“aaaaaaaaa”和“cabcbabcbabcba”。事实上，我们可以利用回文对称的性质来避免一些不必要的计算。

6.一个时间复杂度为O(n)的解决方案(Manache算法) 

   首先，我们将转换输入字符串S为另一个字符串T，转换的方法是：在字符之间添加‘#’符号。例如，S="abaaba",T="#a#b#a#a#b#a#"。为了找寻最长回文子串，我们需要从每个中心Ti开始拓展，使得T(i-d)...T(i+d)为回文。显而易见，d是这个回文的长度。

    我们使用数组P来存储结果，其中，P[i]是以T[i]为中心的回文的长度，所以P中的最大元素即为最长回文子串的长度，使用上面的例子，我们可以得到P为：

    从P我们立马就可以看出，最长的回文子串为“abaaba”，其长度为P6=6。

    你是否注意到了，在字符之间添加特殊字符‘#’，使得无论是奇长度的回文还是偶长度的回文，都更加好处理了。(回文长度都变为奇数了)。

    现在，你想象一下在回文”abaaba“的中心位置画一根竖线，你会发现数组P中的元素关于这条竖线对称，你可以试试另外的回文，例如”aba“，会发现具有同样的对称性质。这是偶然么？答案是是，也是不是，这由特定的情况决定。但是我们从这里开始取得了一个大进步，我们可以消除计算P的某些步骤。

    让我们看一个更加随机的例子，S = “babcbabcbaccba”.

    

    上图展示了字符串T（从S = “babcbabcbaccba”转换而来），假设我们处在一个P已经被部分计算的状态下，实线的位置表示了回文”abcbcbcba“的中心C，两个虚线分别表示了该回文的左边缘L和右边缘R。我们已经计算到i位置了，i位置关于C的对称位置为i‘。考虑下我们如何有效计算P[i]？首先，我们看i’索引的位置，i‘=9.

    其中，在索引之上的两条绿色实线分别覆盖了以i和i’为中心的两个回文区域。P[i']=P[9]=1。根据回文的对称性可知，P[i]也为1。实际上，C位置后的3个元素都可以根据对称性获得。（P[12]=P[10]=0，P[13]=P[9]=1，P[14]=P[8]=0）。

    然而，P[15]并不等于P[7]。如果以T15为中心拓展回文，其结果为”a#b#c#b#a“，显然比P[7]小，这又是怎么造成的呢？

     上图中，有颜色的线段表示以i和i’为中心的回文区域。其中，利用回文根据中心C的对称性，绿实线部分肯定是完全匹配的；红实线部分表示两头可能不会匹配的部分；虚线部分表示跨越回文中心的区域，显然这部分也是相互对称的。我们主要关心以i‘为中心的回文超过左边缘L的部分（红色实线部分），这部分不再遵循对称性质。因为P[i']为7，其在以C为中心的回文中的回文长度为5，根据回文的对称性，P[i]>=5，对照上图实际情况，P[i]=5。

     让我们对上面情况做一个总结，这也是本算法的关键部分：

    :情况1：如果P[i’]<=R-i，即以i’为中心的回文子串包含在以C为中心的回文子串中，由于i和i‘关于C对称，所以以i为中心的回文子串也将包含在以C为中心的回文子串中，所以P[i]>=P[i']，若P[i]>P[i']，显然表示以i为中心的回文子串还可以继续向右匹配，根据对称性，以i‘为中心的回文子串也将可以继续向左匹配，与条件相矛盾，所以P[i]=P[i']。

     情况2：如果P[i’]>R-i,则我们需要拓展右边界R以得到P[i]的值。

     最后的步骤是：判断什么时候向右移动C和R。结论是：如果以i为中心的回文可以拓展超过R，我们将更新回文的中心为i，然后再拓展其右边界R。

     总结：在该算法的每一个步骤中，都存在两种可能，如果P[i’]<=R-i，我们将P[i]=P[i']。否则，我们将改变回文的中心位置为i，并从中心开始拓展R边界，拓展R将至多花费N步骤。另外，定位和测试中心位置最多也只要花费N步骤。因此，算法将在至多2N步骤内完成，即为一个线性的解决方案。

    代码如下：

public class Solution {
    // Transform S into T.
    // For example, S = "abba", T = "^#a#b#b#a#$".
    // ^ and $ signs are sentinels appended to each end to avoid bounds checking
    public String preProcess(String s) {
    	int n = s.length();
    	if (n == 0) return "^$";
    	String ret = "^";
    	for (int i = 0; i < n; i++)
    		ret += "#" + s.charAt(i);
   
    	ret += "#$";
    	return ret;
    }
   
    public String longestPalindrome(String s) {
    	String T = preProcess(s);
    	int n = T.length();
    	int[] P = new int[n];
    	int C = 1, R = 1;
    	for (int i = 1; i < n-1; i++) {
    		int i_mirror = 2*C-i; // equals to i' = C - (i-C)
      
    		P[i] = Math.min(R-i, P[i_mirror]);
      
    		// Attempt to expand palindrome centered at i
    		while (T.charAt(i + 1 + P[i]) == T.charAt(i - 1 - P[i]))
    			P[i]++;
   
    		// If palindrome centered at i expand past R,
    		// adjust center based on expanded palindrome.
    		if (i + P[i] > R) {
    			C = i;
    			R = i + P[i];
    		}
    	}
   
    	// Find the maximum element in P.
    	int maxLen = 0;
    	int centerIndex = 0;
    	for (int i = 1; i < n-1; i++) {
    		if (P[i] > maxLen) {
    			maxLen = P[i];
    			centerIndex = i;
    	}
    }

    return s.substring((centerIndex - 1 - maxLen)/2, (centerIndex - 1 - maxLen)/2+maxLen);
  }
    	 
}

    本算法是利用已经检测过的回文的长度，并根据回文的对称性来减少计算量。

    本文的代码为验证过的java代码。翻译的不是特别好，但是意思差不多都到了的，如果看不懂，可以对照英文原文看。另外，关于Manache算法，可以看看http://www.cnblogs.com/TenosDoIt/p/3675788.html这篇文章。