通用的三视图和正等轴测图的绘制（C++实现）

//实验名称：三视图和正轴测图的绘制
//功       能：对于用户输入的有序空间坐标点数组，绘制这些点所组成的三维立体图形的三视图和正等轴测图（函数可以通用，本题中为了演示选择了一个固定的三维物体）
//编译环境：Visual Studio 2022，EasyX_20220116
#include<iostream>
#include<graphics.h>
#include<conio.h>
using namespace std;
const int gap = 20;//为了使得展示三视图效果时三个视图不重叠，因此用一个间隔将各个视图相互隔开一定距离

//定义一个通用函数用于绘制任意三维物体的三视图并有较好的展示效果，只需要给定空间点对和点的总数即可
void ThreeViews(const int* X, const int* Y, const int* Z,const unsigned& num)
{
	POINT* FrontView=new POINT[num];
	//为了方便展示以及纵坐标负半轴图形的绘制，将坐标原点移动到绘图面板中心并使得纵坐标轴取反方向（其实就是一个坐标轴的变换过程）
	for (unsigned i = 0; i < num; i++)
	{
		FrontView[i].x = X[i] + 500 + gap;//横坐标本身不变，但是由于坐标系变换需要加上500，又因为展示效果的美观加上一个间隔GAP
		FrontView[i].y = 350 - Z[i] - gap;//纵坐标轴的方向取反并且坐标原点改变，因此需要转换纵坐标值而不是取原值
	}

	//定义一个点数组存储正视图的点坐标
	POINT* SideView=new POINT[num];
	for (unsigned i = 0; i < num; i++)
	{
		SideView[i].x = Y[i] + 250 - gap;//处理原因与上面正视图的类似
		SideView[i].y = 350 - Z[i] - gap;
	}
	//定义一个点数组存储俯视图的点坐标
	POINT* VerticalView=new POINT[num];
	for (unsigned i = 0; i < num; i++)
	{
		VerticalView[i].x = X[i] + 520;
		VerticalView[i].y = 600 - Y[i]+gap;
	}

	initgraph(1000, 700);
	//分别作出两条相互垂直的经过绘图中心的直线作为横纵坐标轴
	line(0, 350, 1000, 350);
	line(500, 0, 500, 700);
	setcolor(GREEN);
	//画出正视图（在第一象限内）
	for (unsigned i = 0; i < num - 1; i++)
	{
		line(FrontView[i].x, FrontView[i].y, FrontView[i + 1].x, FrontView[i + 1].y);
	}
	_getch();
	//画出侧视图（在第二象限内）
	for (unsigned i = 0; i < num - 1; i++)
	{
		line(SideView[i].x, SideView[i].y, SideView[i + 1].x, SideView[i + 1].y);
	}
	_getch();
	//画出俯视图（在第三象限内）
	for (unsigned i = 0; i < num - 1; i++)
	{
		line(VerticalView[i].x, VerticalView[i].y, VerticalView[i + 1].x, VerticalView[i + 1].y);
	}
	_getch();
	closegraph();
	//最后不要忘记释放堆内的内存空间
	delete[]FrontView;
	delete[]SideView;
	delete[]VerticalView;
	return;
}

//定义通用的求三维图形的正等轴测图的函数，只需要给定点拓扑排序的坐标和点拓扑排序的个数即可
void PositiveAxonometric(const int* X, const int* Y, const int* Z,const unsigned& num)
{
	initgraph(1000, 700);
	line(0, 350, 1000, 350);
	line(500, 0, 500, 700);
	setcolor(YELLOW);//用黄色绘制正等轴测图用于区分之前用绿色绘制三视图
	POINT *p=new POINT[num];
	//求正等轴测变换后的点坐标有现成的公式，直接套用即可
	for (unsigned i = 0; i < num; i++)
	{
		p[i].x = 0.7071 * X[i] - 0.7071 * Y[i] + 500;
		p[i].y = 350+ 0.4082 * X[i] + 0.4082 * Y[i] - 0.8165 * Z[i];
	}
	//求出坐标后进行直线绘图即可
	for (unsigned i = 0; i < num-1; i++)
	{
		line(p[i].x, p[i].y, p[i + 1].x, p[i + 1].y);
	}
	_getch();
	closegraph();
	delete[]p;//最后不要忘记释放堆内的内存空间
	return;
}

int main(void)
{
	//有序的空间坐标数组是本题的关键，因为需要物体经过三维投影后各点之间仍然保持原有的拓扑排序关系，因此此处对有序点对的定义为：按照三个坐标数组给定的点顺序，能够”不抬笔地”
	//完整绘制出正确的三维物体
	int X[33] = { 0,0,0,0,0,0,0,0,100,100,0,100,100,100,100,100,100,100,100,0,0,0,0,100,100,100,100,0,0,0,0,100,100 };
	int Y[33] = { 0,0,250,250,200,150,0,0,0,0,0,0,150,200,250,250,0,0,150,150,0,150,200,200,150,200,250,250,200,250,250,250,250 };
	int Z[33] = { 100,0,0,50,50,100,100,0,0,100,100,100,100,50,50,0,0,100,100,100,100,100,50,50,100,50,50,50,50,50,0,0,50 };
	cout << "由以上点可以作出该物体的三视图如下所示：(按任意键继续，绘图过程中按任意键进行下一步绘图）";
	_getch();
	ThreeViews(X, Y, Z, 33);
	cout << endl;
	cout << "接着可以作出正等轴测投影图如下所示：（按任意键继续）";
	_getch();
	PositiveAxonometric(X, Y, Z, 33);
	cout << endl;
	return 0;
}

用于测试的三维图形如图所示：

三视图绘制效果：

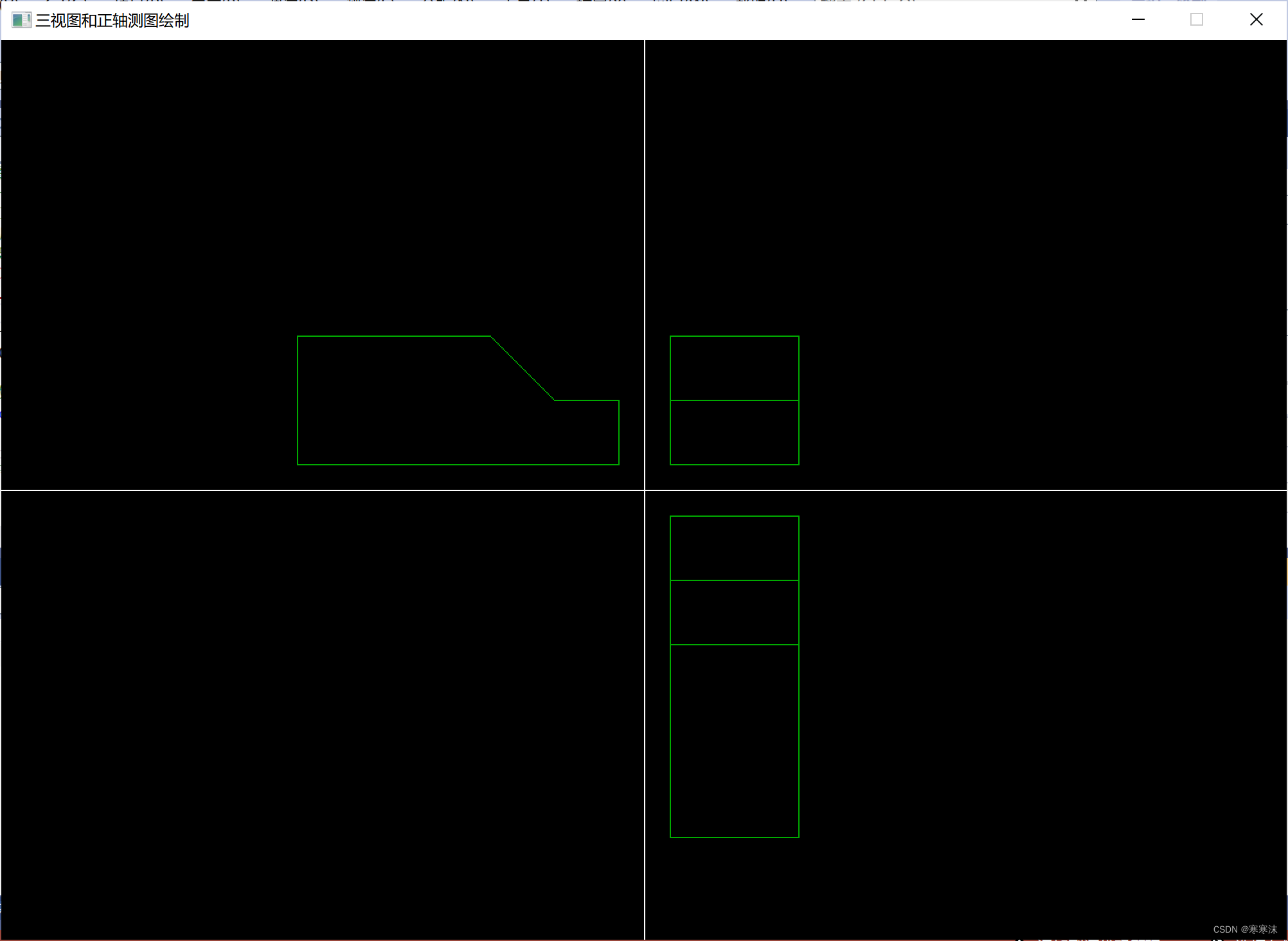
正等轴测图绘制效果：