TDADL-IE：一种用于医学图像安全深度学习驱动密码架构

大家读完觉得有帮助记得关注和点赞！！！

摘要​

数字医学成像（如MRI和CT）的兴起，在远程医疗和云存储中，需要强大的加密技术来保护患者数据。混沌系统因其敏感性和独特特性而广泛应用于图像加密，但现有方法通常缺乏足够的安全性。本文提出了基于三个关键要素的三维扩散算法与深度学习图像加密系统（TDADL-IE）。首先，我们提出了一种增强的混沌生成器，使用带有一维正弦二次混沌映射（1D-SQCM）的LSTM网络，以生成更好的伪随机序列。其次，应用一种新的三维扩散算法（TDA）来加密置乱后的图像。TDADL-IE适用于任何尺寸的图像。实验证实了其对抗各种安全威胁的有效性。代码可在 https://github.com/QuincyQAQ/TDADL-IE获取。

​关键词：​​ 图像加密，混沌系统，深度学习，三维扩散，医学图像安全

​1. 引言​

医学成像和远程医疗的兴起增加了对安全数字图像传输和存储的需求。MRI、CT和超声等医学图像包含对诊断和治疗至关重要的敏感患者数据。没有强大的加密，这些图像容易受到未经授权的访问和泄露，尤其是在不安全的网络或云存储中。保护这些数据对于患者隐私至关重要，并且是HIPAA等法规的要求。传统的面向文本的加密方法由于医学图像的高像素间相关性、大数据量和复杂格式而效果不佳。混沌系统为开发强大而高效的图像加密技术提供了一种有前景的解决方案[1]。

混沌系统以其确定性随机性、遍历性和对初始条件的敏感性而闻名，非常适合密码学应用，例如生成用于图像加密的伪随机序列[2]。尽管一维（1D）混沌映射简单且易于实现[3]，但其可预测性和有限的混沌性可能带来安全风险[2]。因此，研究已转向更复杂的基于混沌的加密系统。最近，深度学习已成为一种新方法，出现了诸如Google Brain使用伴随网络的自加密模型[4]、利用长短期记忆（LSTM）网络评估混沌序列随机性[5]以及混合神经混沌加密方法[6, 7]等努力。尽管取得了这些进展，深度学习在彩色图像加密中的应用，由于其通道间依赖性和高维度的挑战，仍然探索不足。

仅置乱加密方案在图像加密中很常见，但由于密文中可辨别的统计特性，容易受到各种攻击[8]。扩散过程通过模糊局部依赖性来修改像素值以增强加密。许多现有的扩散方案缺乏对明文和密钥变化的敏感性，因为它们独立于图像内容运行。最近的研究集中在明文感知扩散上[9, 10, 11, 12]。Murillo等人使用了基于明文特征的逻辑映射[9]，Parvin等人将XOR操作与混沌函数相结合[10]。然而，这些方法依赖于初始明文进行密钥生成，限制了它们在实时场景（如实时视频加密）中的使用。其弱非线性和有限的密钥空间使它们容易受到选择明文攻击[13, 14]。为了解决这些问题，我们提出了联合非线性三维扩散机制（TDA），它将扩散与图像内容紧密集成，增强了敏感性和雪崩效应。

我们的主要贡献如下：

1. 现有的一维混沌映射经常受到混沌范围受限和对初始条件敏感性欠佳的影响，从而限制了它们在生成安全密码密钥方面的效力。因此，提出了一种新颖的一维混沌映射1D-正弦二次混沌映射（1D-SQCM），它可以生成具有增强随机性和更宽混沌范围的序列。

2. 通过将1D-正弦二次混沌映射（1D-SQCM）与长短期记忆（LSTM）网络的动态建模能力协同整合，我们设计了一种新颖的混沌序列生成器。该生成器表现出扩展的混沌区域、优异的熵和精细的时间相关性，最终实现了显著增强的随机性和密码鲁棒性。

3. 针对扩散非方形和彩色图像的独特需求，其中通道间相关性和变化的维度构成了重大挑战，我们提出了三维扩散算法（TDA）。该机制将前向和后向扩散过程与通道间像素相互作用相结合。这种设计确保了明文的微小变化会在整个密文中级联传播，从而显著增强了密钥敏感性和明文敏感性。

​2. 方法​

TDADL-IE是一种用于多医学图像的新加密算法，使用一维正弦-余弦-指数映射（1D-SQCM）和神经网络增强。其流程图如图1所示。该算法有两个主要模块：（1）使用1D-SQCM和BLSTM网络生成混沌序列，以及（2）三维扩散算法（TDA）。TDADL-IE可以同时加密多个图像。加密的密钥是Keyx1, Keyy1, Keya, 和 KeyN0。这些模块在以下小节中详细说明。

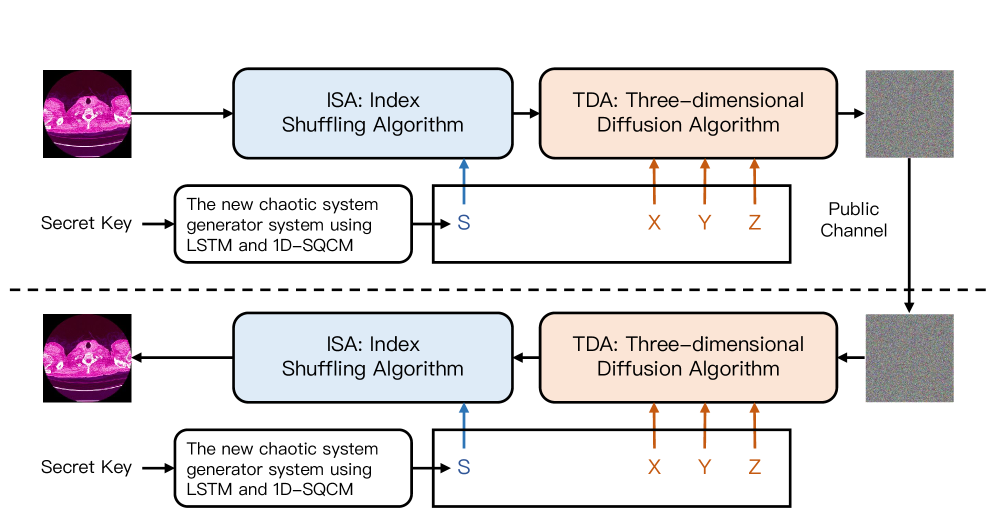
图1：加密算法的过程。

​2.1 使用1D-SQCM和BLSTM生成混沌序列​

双向长短期记忆（BLSTM）网络通过涉及输入门、遗忘门、输出门和记忆单元的设计增强了标准LSTM[15]（LSTM结构如图2所示）。遗忘门ft调节从前一状态ht-1保留的信息，其输出限制在[0,1]范围内。在生成类混沌序列时，遗忘门选择性丢弃历史信息，反映了混沌系统的衰减记忆，增加了对初始条件的敏感性，并鼓励发散相空间轨迹。同时，输入门控制新信息的输入，引入非线性变化，影响系统演化并增强复杂动力学。记忆单元整合这些输入，更新其状态以捕获长期依赖性并产生复杂的、高维的序列。总之，这些元素形成了一个强大的非线性机制，用于建模和创建具有混沌特征的复杂时间序列。

利用这些特性，我们引入了一种混合混沌序列生成器，它协同结合了一维正弦-余弦-指数映射（1D-SQCM）与BLSTM网络的时间建模能力。选择1D-SQCM是因为其固有的高熵和对初始条件显著敏感的特性，其定义如下：

其中xn表示第n次迭代的状态变量，a是系统控制参数。随后通过BLSTM网络处理1D-SQCM的输出，我们的目标是生成不仅时间相关、统计丰富，而且表现出显著相空间发散的序列。这种集成方法保留了混沌映射的基本随机性，同时使BLSTM能够自适应地学习并放大生成序列的复杂性和不可预测性。

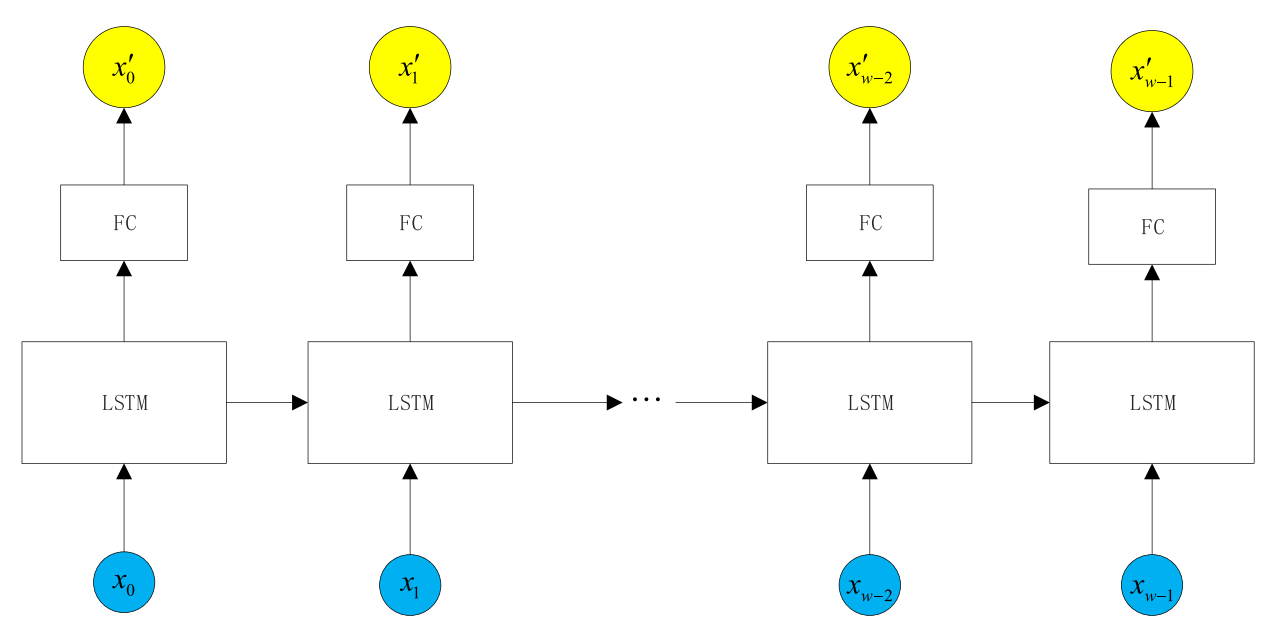
（图2：LSTM训练模型图。a x的训练图）

步骤1：BLSTM模型训练。BLSTM模型经过初始训练阶段以学习混沌序列的复杂动力学。此过程如下开始：

1. 训练数据生成：指定1D-SQCM（公式1）的系统参数Keya和初始状态Keyx0（不同于用于图像处理的加密密钥）。迭代1D-SQCM以生成原始混沌序列。为减轻瞬态效应并确保序列在混沌吸引子内运行，丢弃初始Ndiscard_train=6,000次迭代。收集随后的Ntrain=24,000个点形成训练序列，记为Xtrain。

2. BLSTM配置与训练：定义BLSTM网络的架构，包括隐藏层和单元的数量。优化关键超参数，例如学习率和用于训练的输入子序列长度。然后使用Xtrain训练BLSTM模型，以学习其潜在的时间模式和统计特性。

训练阶段完成后，BLSTM模型便具备为加密过程生成增强混沌序列的能力。

步骤2：用于加密的混合混沌序列生成。对于加密过程，使用密钥Keyx1, Keyy1, Keya, 和 KeyN0。生成过程如下：

1. 1D-SQCM序列生成：使用1D-SQCM（公式1）生成长度为2mn的主混沌序列，记为XSQCM。该映射使用Keyx1作为初始状态x0进行初始化，Keya作为控制参数。密钥Keyy1和KeyN0可能影响某些方面，例如在为加密收集序列值之前要丢弃的初始迭代次数。

2. BLSTM序列增强：然后使用训练好的BLSTM模型产生次生混沌序列XBLSTM，长度也为2mn。该序列可以通过将初始种子（从密钥或XSQCM的片段派生）馈送到BLSTM并让其预测后续值来生成。

3. 序列连接：将两个序列XSQCM和XBLSTM水平连接，形成总长度为4mn的混合混沌序列S hybrid。这种混合序列受益于1D-SQCM的基本混沌特性和BLSTM引入的学习复杂性。

长度mn通常对应于尺寸为m×n的图像单通道中的像素数。总长度4mn为处理相当于每像素四个分量（例如RGBA）的m×n图像或用于密码操作的四个不同的m×n序列做准备。

步骤3：混沌序列处理与推导。随后处理步骤2中生成的、长度为4mn的混合混沌序列S hybrid，以推导出用于加密算法各个阶段的定制序列。此处理过程如下：

1. 序列分区：将序列S hybrid划分为四个子序列s, x, y, 和 z，每个长度为L=mn。（这里L=mn表示每个子序列中的元素数量，对应于单通道m×n图像的像素数）。

2. 扩散序列推导：使用LABEL:pre-random中定义的变换，从子序列x, y, 和 z计算三个新序列X, Y, 和 Z，长度也为L=mn。

   

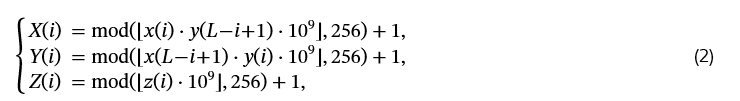
   其中 i=1,2,…,L。

3. 矩阵重塑：将得到的一维序列X, Y, 和 Z重塑为m×n矩阵，分别记为X2D, Y2D, 和 Z2D。这些矩阵随后用于TDA模块。序列s保留给索引混洗算法（ISA）使用。

这种多阶段推导确保为不同的密码操作提供独特、复杂的伪随机序列，从而增强了整体安全性。

​2.2 索引混洗算法（ISA）​​

索引混洗算法（ISA）实现像素级置换，以混淆输入图像内的空间相关性。该过程独立应用于每个m×n图像或图像通道，使用如第II-A节（步骤3）所述推导出的混沌序列s（长度为mn）。ISA过程如下：

1. 向量化：将图像（或其单个通道）的m×n像素数据展平为长度为mn的一维向量P。

2. 置换索引生成：利用混沌序列s导出一组置换索引。常见方法是获取对s元素进行排序所需的索引。设这些索引为Idx = [idx1, idx2, …, idxmn]。

3. 像素加扰：向量P中的像素根据这些索引重新排序。具体来说，置换后向量P'中的第j个像素是P(idxj)。此操作有效地打乱了原始像素排列。

4. 重塑：将置换后的向量P'重塑回其原始的m×n二维结构，产生混洗后的图像（或通道）。

此置换步骤通过去相关相邻像素，显著增强了算法抵抗统计攻击的能力。

​2.3 三维扩散算法（TDA）​​

​算法1 三维扩散算法​

0: 尺寸为M×N的混洗后图像A，以及混沌矩阵X2D, Y2D, 和 Z2D

1: C(1,1,1) ← mod( A(1,1,1) + X2D(1,1), 256 )

2: C(1,1,2) ← mod( A(1,1,2) + Y2D(1,1), 256 )

3: C(1,1,3) ← mod( A(1,1,3) + Z2D(1,1), 256 )

4: for j=2 to N do

5:  C(1,j,1) ← mod( A(1,j,1) + X2D(1,j) + C(1,j-1,1) + C(1,j-1,3), 256 )

6:  C(1,j,2) ← mod( A(1,j,2) + Y2D(1,j) + C(1,j-1,2) + C(1,j-1,1), 256 )

7:  C(1,j,3) ← mod( A(1,j,3) + Z2D(1,j) + C(1,j-1,3) + C(1,j-1,2), 256 )

8: end for

9: for i=2 to M do

10:  C(i,1,1) ← mod( A(i,1,1) + X2D(i,1) + C(i-1,1,1) + C(i-1,1,3), 256 )

11:  C(i,1,2) ← mod( A(i,1,2) + Y2D(i,1) + C(i-1,1,2) + C(i-1,1,1), 256 )

12:  C(i,1,3) ← mod( A(i,1,3) + Z2D(i,1) + C(i-1,1,3) + C(i-1,1,2), 256 )

13: end for

14: repeat

15:  for i=2 to M do

16:   for j=2 to N do

17:    C(i,j,1) ← mod( A(i,j,1) + X2D(i,j) + C(i,j-1,3) + C(i-1,j,3), 256 )

18:    C(i,j,2) ← mod( A(i,j,2) + Y2D(i,j) + C(i,j-1,1) + C(i-1,j,1), 256 )

19:    C(i,j,3) ← mod( A(i,j,3) + Z2D(i,j) + C(i,j-1,2) + C(i-1,j,2), 256 )

20:   end for

21:  end for

22: until 图像加密过程完成。

23: Output: 加密图像C

三维扩散算法（TDA）旨在将像素信息扩散到图像的空間维度和颜色通道中。它使用前向和后向扩散通道来确保对单个明文字符的更改会影响许多密文字符，从而保证扩散效应。前向通道按光栅顺序（例如从左上角(1,1)到右下角(m,n)）处理像素，而后向通道则按相反方向（例如从(m,n)到(1,1)）处理。

TDA的跨通道像素相互作用通过确保扩散发生在颜色平面之间，增强了加密强度，特别是对于彩色图像。概念上如图3所示，一个通道中的像素受到其他通道中相邻像素的影响。例如，在扩散过程中，位于(i,j)的绿色（G）通道像素使用附近的红色（R）通道像素（例如来自(i-1,j)和(i,j-1)）、其先前的G邻居以及一个密钥派生的元素进行更新。蓝色（B）通道像素也可能依赖于G通道值。这种通道间依赖性对于抵消独立通道分析至关重要。TDA的操作和更新在算法1中有详细说明，使用了密钥相关的矩阵X2D, Y2D, 和 Z2D。

（图3：三维扩散算法（TDA）示意图）

​2.4 解密算法​

TDADL-IE的解密过程设计为加密过程的精确逆过程。鉴于核心操作——混沌序列生成、索引混洗（置换）和三维扩散（通常涉及XOR和模运算等操作）——是确定性的且可逆的（当使用正确的密钥（Keyx1, Keyy1, Keya, KeyN0）时），可以完美重建原始明文图像。解密包括：

1. 混沌序列再生：使用与加密阶段相同的密钥，完全相同地再生同一组混沌序列（s, X2D, Y2D, Z2D）。

2. 逆三维扩散：以相反的顺序应用TDA操作。这通常涉及按扩散通道的逆序（例如，先逆向后向通道，再逆向前向通道）进行处理，并应用每个加密操作的数学逆运算（例如，XOR是自逆的；模加法对应模减法）。跨通道依赖性也根据定义的逆规则进行反转。

3. 逆索引混洗：将逆置换（从相同的混沌序列s通过确定索引的逆映射导出）应用于扩散后的图像，以恢复原始像素顺序。

明文图像的成功恢复取决于这些逆步骤的精确应用以及所使用的与加密时相同的密钥的可用性。

​3. 实验结果​

本节评估所提出的密码系统，重点评估TDADL-IE算法的效率和安全性以及1D-SQCM混沌映射的性能特征。

​3.1 实验设置​

验证包括分析一维正弦-余弦π超混沌映射（1D-SQCM）和评估TDADL-IE加密算法。将1D-SQCM的混沌行为与三种一维混沌映射（表I）和二维系统进行比较。对于TDADL-IE，使用三幅标准灰度测试图像“IMG1”、“IMG2”和“IMG3”，尺寸为M×N，例如512×512像素[16]。使用标准度量将其与最先进的加密技术[17, 18, 19, 20, 21]进行比较。实验在AMD Ryzen 7 7800X3D CPU @ 4.20 GHz、32 GB RAM、Windows 11和MATLAB R2024a环境下运行。

​3.2 1D-SQCM混沌映射的性能分析​

本小节对提出的1D-SQCM与其他现有混沌映射所表现的混沌动力学进行了比较分析，详细比较见表I。目的是证明1D-SQCM增强的混沌特性。

​表I：测试的映射。​​

名称	数学表达式	参数设置
1D-SQCM	xn+1 = sin(a sin(xn))	a ∈ (0, ∞)
sine	xn+1 = b × sin(π xn)	b ∈ (0, ∞)
1-DFCS	xn+1 = cos((η xn+1)^2+1) sin((η xn+1)^2+1) + 2	η ∈ (0, ∞)
1D-Chebyshev	xn+1 = cos(k × arccos(xn))	k ∈ (0, ∞)

​3.2.1 Lyapunov指数分析​

Lyapunov指数（LE）量化动力系统对其初始条件微小扰动的敏感性，正LE表示混沌行为。图4展示了对控制参数范围(0,10000)内，1D-SQCM和其他基准一维混沌映射的Lyapunov指数。结果表明，1D-SQCM在整个范围内保持正的Lyapunov指数。此外，这些值 consistently 大于比较的混沌映射，表明了强大的混沌特性和对初始条件的高度敏感性，这对于密码学应用是可取的。

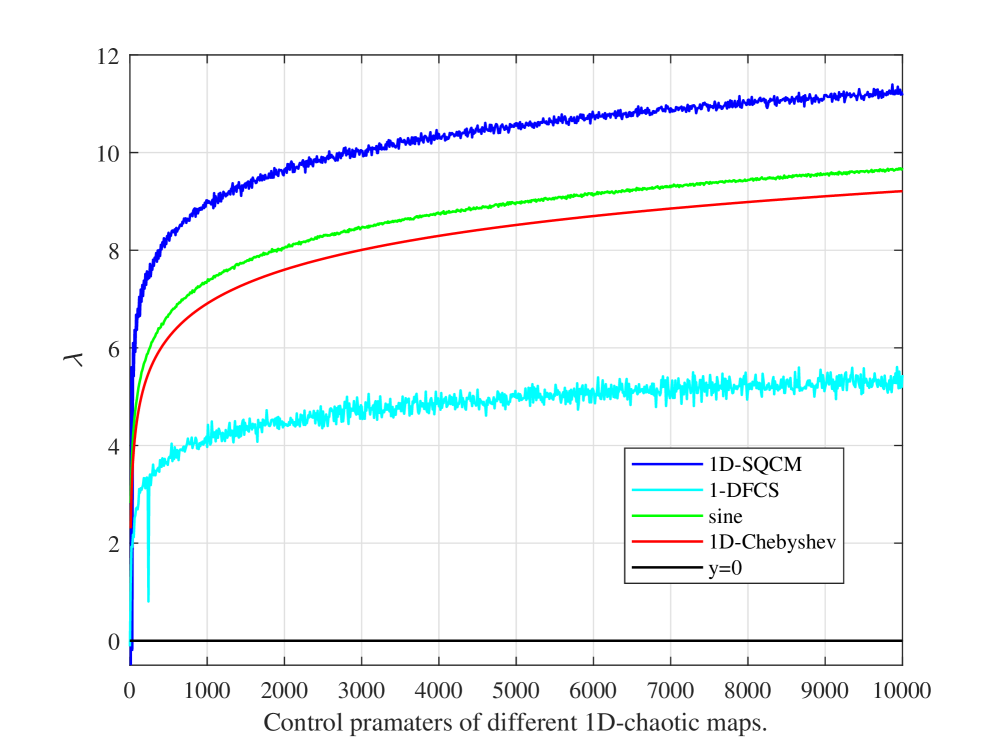
（图4：1D-SQCM、1-DFCS、Sine和1D-Chebyshev映射的Lyapunov指数。）

​3.2.2 NIST SP 800-22统计测试套件​

使用NIST SP 800-22统计测试套件严格评估了1D-SQCM生成序列的随机性。该套件包含一组旨在检测二进制序列与真实随机性偏差的测试。表II展示了将这些测试应用于从1D-SQCM输出导出的序列所获得的P值。对于所有生成的序列，P值 consistently 超过0.01的标准显著性阈值。

​表II：1D-SQCM的NIST测试结果。​​

测试索引	测试名称	P值	结果
1	频率（单比特）测试	0.0909	PASS
2	块内频率测试	0.0711	PASS
3	游程测试	0.2368	PASS
4	块内最长1游程测试	0.4190	PASS
5	二进制矩阵秩测试	0.7981	PASS
6	离散傅里叶变换（频谱）测试	0.3504	PASS
7	非重叠模板匹配测试	0.2368	PASS
8	重叠模板匹配测试	0.2757	PASS
9	Maurer通用统计测试	0.9780	PASS
10	线性复杂度测试	0.8676	PASS
11	序列测试	0.8343	PASS
12	近似熵测试	0.5341	PASS
13	累积和（Cusums）测试	0.2896	PASS
14	随机游走测试	0.8623	PASS
15	随机游走变体测试	0.8676	PASS

​3.2.3 基于深度学习的可预测性评估

​

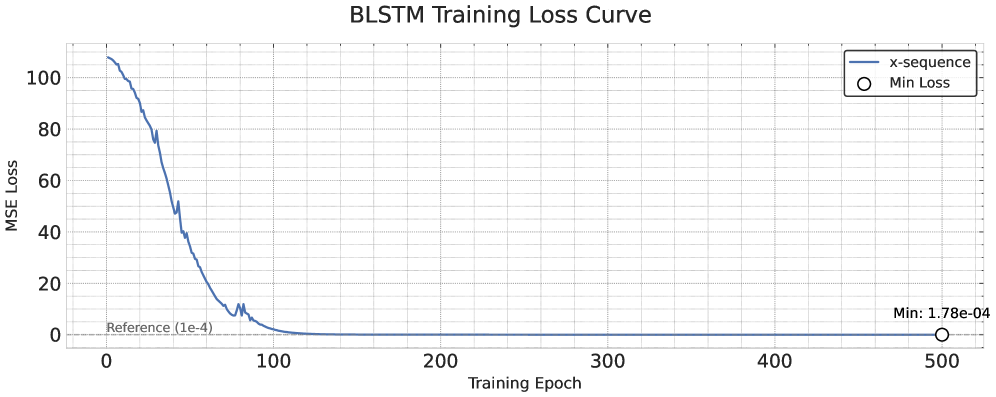
（图5：BLSTM训练损失）

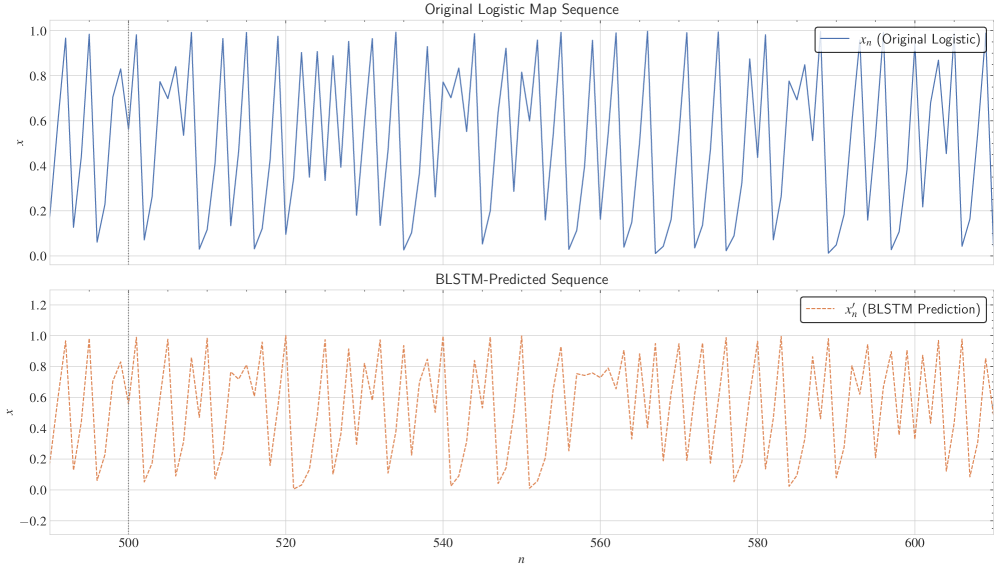
（图6：混沌信号的差异。）

使用双向长短期记忆（BLSTM）网络分析了1D-SQCM的输出，训练细节见图6。低均方根误差（RMSE）和损失函数值表明BLSTM能够学习混沌序列的短期模式。图6展示了实际序列{Xtrue}与BLSTM预测{Xpred}之间的比较。{Xtrue}和{Xpred}在长期预测上的差异突显了1D-SQCM的长期不可预测性，这是强大混沌系统的特征。

​3.3 TDADL-IE密码系统的安全与性能分析​

​3.3.1 密钥空间分析​

抵抗穷举搜索攻击的鲁棒密码安全性的一个基本要求是密钥空间显著大于2^100。TDADL-IE密码系统使用四个密钥，其初始理论范围如下：Keyx1 ∈ (0,1), Keyy1 ∈ (0,1), Keya ∈ (0,∞), 和 KeyN0 ∈ (2000,∞)。在实际的数字实现中，这些连续范围基于数值表示的精度进行离散化。因此，有效的离散密钥空间是巨大的，估计约为2^208。这显著超过了上述安全阈值，使得暴力攻击在计算上不可行，从而提供了高水平的保护。

​3.3.2 差分攻击分析：明文和密钥敏感性​

加密算法对差分攻击的韧性通过其对明文或密钥微小变化的敏感性来衡量，通过NPCR和UACI指标进行评估。对于具有类随机密文的8位灰度图像，理想的NPCR和UACI值分别约为99.6%和33.4%。TDADL-IE算法在改变单个比特时的NPCR和UACI得分很高且接近这些理想水平，表明其具有强大的扩散特性和对差分密码分析的鲁棒性（表III）。

​表III：一种图像的相关方案系数比较。​​

算法	相关系数	信息熵 ↑	时间 (s) ↓	NPCR	UACI	密钥空间 ↑
	水平(H) 垂直(V) 对角(D)
提出的	0.0011 -0.0009 0.0016	7.9993	0.3814	99.6094(*)	33.4641(*)	2^208
Kamal 等人[21]	0.0145 0.0115 0.0087	7.9992	3.0901	99.6010	33.4389	2^115
Ye 等人[22]	0.0085 -0.0056 0.0040	7.9992	3.3714	99.6132	33.4268	2^156
Xu 等人[23]	0.0067 -0.0086 0.0140	7.9935	0.5509	99.6102	33.4812	2^30
(*此值最接近理想值)

​3.3.3 相关系数分析​

明文图像在相邻像素间显示出高度相关性。一个有效的加密算法应该减少密文中的这些相关性，防止统计攻击。表III显示，虽然原始图像具有很强的相关性，但TDADL-IE加密后的图像在所有方向上的相关系数都接近于零。这种减少表明TDADL-IE有效地去相关了像素值，增强了对统计密码分析的安全性。

​3.3.4 加密效率​

计算效率对于图像加密算法的实用性至关重要。在指定环境中评估了TDADL-IE方案的加密速度，并与[17, 18, 19, 20, 21]中的其他算法进行了比较。根据表III，它以有竞争力的速度处理图像，证明了其对于需要及时处理的应用的效率和适用性。

​4. 结论​

本文提出了一种新颖的彩色图像加密方法，解决了密钥和明文敏感性低的问题。该方法使用一个新的一维混沌系统（1D-SQCM）和双向扩散算法（TDA）来实现高安全性和效率。1D-SQCM生成伪随机序列，索引混洗算法（ISA）在置换阶段重新排列像素数据。TDA确保明文的修改被彻底扩散，增强了安全性和效率。实验表明了对攻击的强大抵抗力，确立了该方法作为一种有效且安全的数字图像加密方法。