【CSP-J2022年】解密题解

1.60分做法

        作为一个不擅长数学的选手，你也一定要在比赛中拿到60分的暴力分。暴力做法很容易想到，下面就直接出示代码了。

#include <cstdio>
#include <iostream>
using namespace std;
void MAIN(){
    long long n,d,e;
    bool f=false;
    cin>>n>>d>>e;
    long long sum=n-(e*d-2);
    for (long long i=1;i*i<=n;i++){
        if (n%i==0 && i*sum-i*i==n){
            cout<<i<<" "<<n/i<<endl;
            f=true;
            break;
        }
    }
    if (!f) cout<<"NO\n";
}
int main(){
    int k;
    cin>>k;
    while(k--) MAIN();
    return 0;
}

2.满分做法

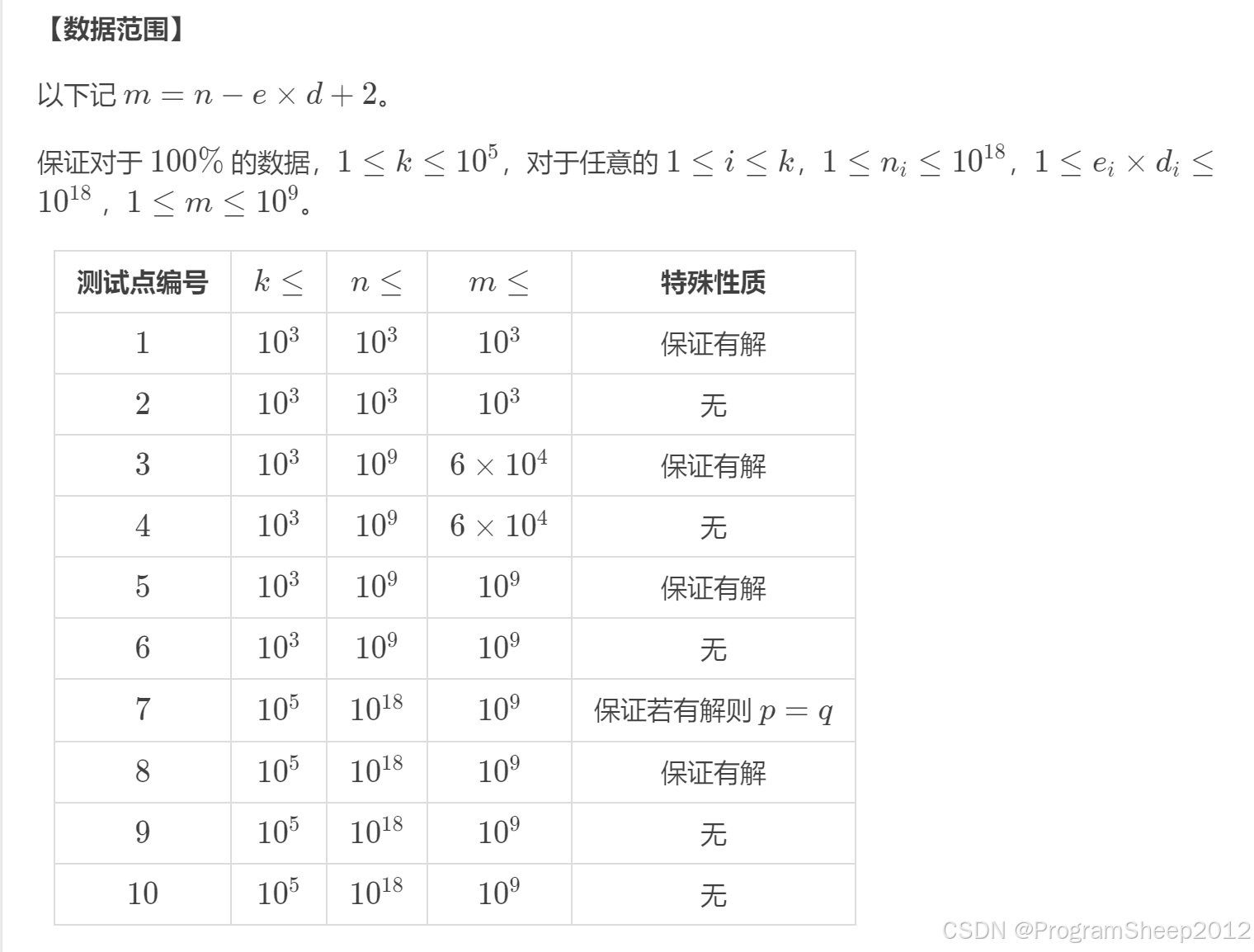
        认真分析数据范围的读者一定会发现这道题的数据范围光是k就有10^5那么庞大，那么对于我们每一次的询问只有想出O(1)的时间复杂度才能拿到满分。

        那么想要在O(1)的时间完成每次任务，不能想到一定要通过数学推导得出答案。接下来给大家讲解整道题的数学推到。需要用到关于一元二次方程的知识。

首先对于ed=(p-1)(q-1)+1，我们可以先将等号右边的括号去掉

得出ed=pq-p-q+2，接着将p和q移到等号左边，其余放在等号右边

得出p+q=pq-ed+2，又因pq=n，我们将pq转换成n

因此我们得出

                ​​​​​​​        

通过第二个式子我们可以将q，转化为n/p

由此可得可将一式变成p+n/p=n-ed+2，我们利用等式性质将等号两边同时乘p

变成p^2+n=p(n-ed+2)

再稍作整理可得p^2-p(n-ed+2)+n=0

不难发现这正是一个一元二次方程，因此我们只要求出这个方程的解，就可以确定出答案。下面我们先来复习一下关于一元二次方程的知识。

我们已知一个一元二次方程ax^2+bx+c=0

那么我们可以计算出=b^2-4ac

最后x=

因此对于本题a=1,b=-(n-ed+2),c=n

本题的=[-(n-ed+2)]^2-4n

最后p和q分别为和。

但是需要特别注意的是当<0时是无解的，要按照题目要求输出NO

通过数学推导我们就可以每次在O(1)的时间完成答案计算，最后总时间复杂度为O(k)，足矣通过本体。

下面附上代码

#include <bits/stdc++.h>
using namespace std;
void MAIN(){
    long long n,d,e;
    cin>>n>>d>>e;
    long long tran=(n-e*d+2)*(n-e*d+2)-4*n;
    if (tran<0){
    	cout<<"NO\n";
    	return ;
	}
    long long p=(-(n-e*d+2)+sqrt(tran))/-2;
    long long q=n/p;
    if (!(n==p*q && e*d==(p-1)*(q-1)+1)){
    	cout<<"NO\n";
    	return ;
	}
    cout<<p<<" "<<q<<endl; 
}
int main(){
    int k;
    cin>>k;
    while(k--) MAIN();
    return 0;
}