TensorFlow笔记（四）Word2Vector详解

最新推荐文章于 2025-02-13 21:01:53 发布

原创最新推荐文章于 2025-02-13 21:01:53 发布 · 1.4k 阅读

7 ·

CC 4.0 BY-SA版权

文章标签：

#自然语言处理

深度学习专栏收录该内容

12 篇文章

订阅专栏

从N-Gram模型的局限性出发，深入探讨word2vec算法的原理，包括CBOW和Skip-Gram模型，以及Hierarchical Softmax和负采样技术，最后通过gensim库实现词向量训练。

一、前言

文本处理处理任务（NLP）是一个在深度学习领域非常常见的任务，同时也是一个非常热门的分支领域。早期的NLP问题主要有文本翻译、词预测等。例如，给出一句话中间少了一个词，预测最可能是什么词。早期的语言模型是基于概率计算的，会去计算在已知前面n个词的情况下，下一个词为某个词的概率，典型的贝叶斯估计。但是，这会有一个很大的问题，就是计算复杂、数据稀疏，严重依赖语料库的样本语料分布，词同时出现的情况可能没有，组合阶数高时尤其明显，就会出现概率为0的情况。

二、N-Gram

鉴于上述问题，我们引入马尔科夫假设：一个词的出现仅与它之前的 i 个词有关。即下面条件成立：

$p(w_{n}|w_{n-1}w_{n-2}...w_{1}) = p(w_{n}|w_{n-1}w_{n-2}...w_{n-i}) (i<n-1)$

最简单的情况，如果一个词的出现仅依赖于它前面的一个词，那么我们就称之为 Bi-gram：

如果一个词的出现仅依赖于它前面的两个词，那么我们就称之为 Tri-gram：

在实践中用的最多的就是bigram和trigram了，而且效果很不错。高于四元的用的很少，因为训练它需要更庞大的语料，而且数据稀疏严重，时间复杂度高，精度却提高的不多。

上面概率p的计算方法也非常简单，就是简单的频率统计计算（极大似然估计）。以Bi-gram为例，统计样本中所有词组的次数就可以了。例如下面三句话组成的文本库：

I出现3次，I后am的次数为2，所以 p(am | I) = 2/3。

另外再提供一个《Language Modeling with Ngrams》中的例子，Jurafsky et al., 1994 从加州一个餐厅的数据库中做了一些统计：

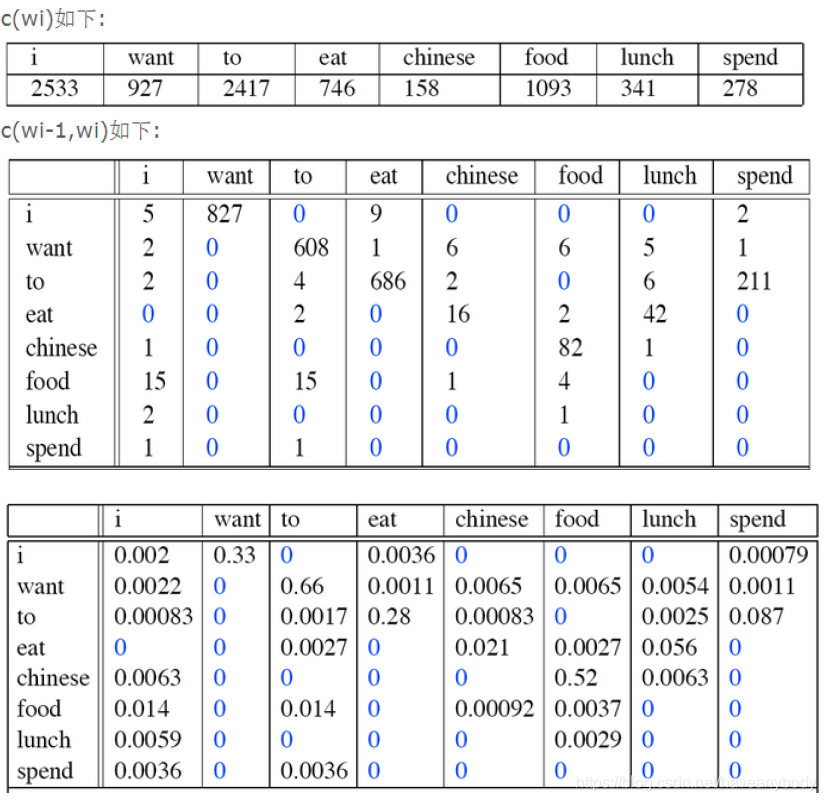
I want chinese food这句话出现的概率为：

p(I want chinese food)=P(want|I)×P(chinese|want)×P(food|chinese)=0.33 * 0.0065 * 0.52

上面的概率相乘很可能造成数据下溢（downflow），即很多个小于1的常数相乘会约等于0，此时可以使用log概率解决。另外还有一个重要的问题就是上面表格中出现了很多概率为0的组合，如果计算概率文本中出现了lunch spend，因为 p(lunch | spend) = 0，就会导致这句话的概率为0。常见的处理方法包括给每个未出现的词组次数都加1，即计算频率的时候分子分母都加1，保证所有的概率都不为0，或者给每个为0的概率都赋予一个非常小的值（即分子分母都加一个大于0小于1的数），也是为了保证在概率和为1的基础上，不出现概率为0的情况。关于更多的处理方法，可以参考最后一篇参考资料。

关于N-gram的训练数据，如果你以为只要是英语就可以了，那就大错特错了。文献《Language Modeling with Ngrams》的作者做了个实验，分别用莎士比亚文学作品，以及华尔街日报作为训练集训练两个N-gram，他认为，两个数据集都是英语，那么用他们生成的文本应该也会有所重合。然而结果是，用两个语料库生成的文本没有任何重合性，即使在语法结构上也没有。这告诉我们，N-gram的训练是很挑数据集的，你要训练一个问答系统，那就要用问答的语料库来训练，要训练一个金融分析系统，就要用类似于华尔街日报这样的语料库来训练。

N-gram的特性可以用来处理分词、翻译、纠错等问题，因为通常情况下，一句经常出现的话，一定比一句有错误的话计算概率要高。例如，在语音识别中，“吃饭”和“赤饭”肯定是前一句的概率更高，在分词过程中“我喜欢你”，正确的分词结果是“我/喜欢/你”，而不是“我喜/欢你”，因为肯定是前一句话概率高。

在N-Gram后续过程中还出现了NNLM（Neural Network based Language Model）、RNNLM等升级版模型，已经是和word2vector很像的处理方法，因为不是本文重点这里就不再具体介绍了。

三、word2vector

word2vector是google提出的一种词嵌入（word embedding，又叫词向量）算法，何谓词向量呢？在自然语言处理领域，输入一般都是文字，但是对于计算机来说，它并不认识文字，必须要转化为数学符号，也就是数字才行。在机器学习领域，这个操作也叫特征工程。既然有了N-Gram，为什么还会有word2vector呢？首先，N-Gram基于统计概率的处理方法可以用来判断一个句子的概率，或者在输入法中判断下一个可能的词，但是不能用来在实际中预测下一个词，因为他的预测结果永远是训练样本中频率最大的那一个。另外，N-Gram是将词作为一个个独立的个体来对待的，这种处理方式等价于one-hot编码和词袋(Bag Of Words)模型，我们有N个词，我们的词向量就有N维，且是独热的形态。

例如，我们有一个评论分类任务，用户评价是好评还是差评，“我喜欢这个产品”这句话有四个词：我、喜欢、这个、产品，怎么变成程序可识别的输入呢？我们可以借鉴one-hot思想，四个词，做ont-hot分别是：[1,0,0,0]、[0,1,0,0]、[0,0,1,0]、[0,0,0,1]，这样就完成了特征转换。但是我们可以发现这种操作存在很大的问题，现在我们有四个词，所以词向量的长度是4，实际中我们可能有成千上万的词，那么我们构建的one-hot词向量长度就会很长，并且因为大多数元素都是0，所以每个文本的词向量集就是一个非常稀疏的矩阵。另外，因为one-hot的特殊性，任意两个词的编辑距离都是2，欧式距离平方也是2，也即特显不出词与词之间的关系，例如：“优秀”、“很好”和“糟糕”，显然前两个词的含义应该是很近的，最后一个和前两个差别比较大，但是one-hot后，差别都一样。再例如，“我要去网吧”和“我要去网咖”，实际意思一样，但是如果在训练样本中“去网吧”出现的次数远比“去网咖”多，那么这两句的概率显然会差别很大。为了解决上述问题，word2vector应运而出。既然每个词向量都很稀疏，并且很长，是不是可以使用固定长度的非零词向量来表示每个词呢？例如，设置词向量的长度为2，“优秀”是[1,2]，“很好”是[1.1,1.9]，“糟糕”是[12,18]，可以发现这种方法不仅词向量的长度少了，可以表达的词更多了，而且不同词之间的欧氏距离和余弦相似度还可以表达不同词之间的含义相似度，即word2vector在量化词语的基础上，还蕴含了语义信息。

上面的方法虽然很好，但是我们又面临了一个问题，就是怎么确定每个词的词向量呢？

3.1 CBOW和Skip-Gram

在word2vec出现之前，已经有用神经网络DNN来用训练词向量进而处理词与词之间的关系了。采用的方法一般是一个三层的神经网络结构（当然也可以多层），分为输入层，隐藏层和输出层(softmax层)，主要有CBOW(Continuous Bag-of-Words 与Skip-Gram两种模型。

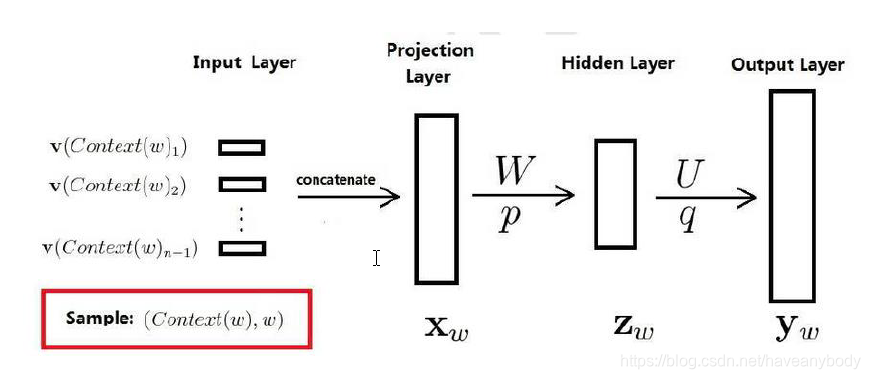
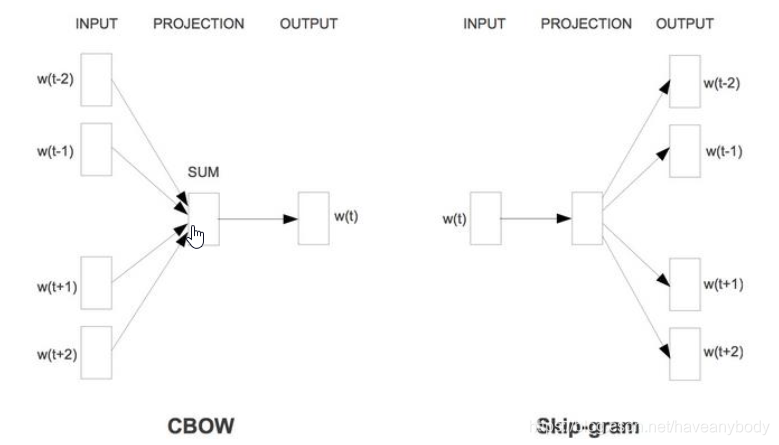
3.1.1 CBOW

CBOW 是Continuous Bag-of-Words Model 的缩写，是一种根据上下文的词语预测当前词语的出现概率的模型，不同于N-Gram，我们不仅仅使用前n个词来判断当前词，一般还会结合后n个词一起预测当前词。CBOW的训练输入是某一个特征词的上下文相关的词对应的词向量，而输出就是这特定的一个词的词向量，即CBOW是使用多个词来预测一个词。比如我们的上下文大小取值为4，即使用前后各4个词预测当前词，模型的输入是8个词向量，并且这8个词都是平等的，也就是不考虑他们和我们关注的词之间的距离大小，只要在我们上下文之内即可。

这里需要明白两个问题，对于理解word2vector异常重要：（1）上面的网络模型细节这里可以不必深究，输入是前后2n个词向量，输出是要预测的这个词向量；（2）对于大多数模型，我们的输入输出都是固定的，只要在训练过程中不断feed即可，最后得到网络参数，但是在word2vector的训练过程中却大不相同，我们的输入输出都是词向量，但是我们的目的也是为了得到词向量，模型在训练的过程中我们会首先给每个词向量随机赋值一个值，同时词向量也参与整个训练过程，并且不断调整。

假如我们的训练样本有100个词，设置词向量的维度为10，即词向量矩阵V大小是[100, 10]。现在有一个训练集 “有力促进了同心县与全国其他地方一道迈向全面小康”，这句话分词结果是 ['有力', '促进', '了', '同心县', '与', '全国', '其他', '地方', '一道', '迈向', '全面', '小康']，以label为“地方”为例，前四个词加后四个词组成的输入是['同心县', '与', '全国', '其他', '一道', '迈向', '全面', '小康']，根据每个词的索引，在V中取出相应的词向量X（大小是[8, 10]），通过神经网络计算和softmax输出后会得到一个对应100个词的概率输出，loss就是这个输出和表示实际label的one-hot的交叉熵损失，然后根据loss去调节神经网络参数和输入X。在该次训练中会同时更新['同心县', '与', '全国', '其他', '一道', '迈向', '全面', '小康']八个词的词向量，虽然“地方”对应的词向量没有被更新，但是在其他输入含有“地方的”样本参与训练的过程中，会被更新。这里我们可以发现：CBOW虽然是使用2n个词预测一个词，但是在训练过程中却是使用一个词去同时调节2n个词的过程（理解这句话很重要）。从整个训练过程我们可以发现，word2vector的训练过程，训练的不仅仅是神经网络中间层的参数，还有输入层X的参数，因此，词向量实际上是模型训练过程中的副产品。

在实际训练过程中，通常会把词向量作为第一个隐藏层（大小是100 * 10的矩阵），输入使用one-hot表示的训练样本，在上面的例子中，就是一个大小为 8*100的one-hot矩阵，乘以词向量矩阵即可得到词向量输入，CBOW在矩阵运算之前会把八个输入词向量做平均处理得到1*10的结果，再乘以隐藏层和softmax处理得到输出，整个处理过程参考下图（这里只使用了一个隐藏层）。训练结束以后，词向量矩阵就是我们需要的结果。因为第一步使用one-hot矩阵乘以词向量矩阵的运算会消耗大量资源，所以大多数情况下是使用下标索引的方法拿到训练词向量矩阵输入。

3.1.2 Skip-Gram

理解CBOW以后，再看Skip-Gram就比较简单了。Skip-Gram是使用当前的中心词来预测上下文2n个词（即前后各n个），就中心词依次和前后2n个词组成2n个训练样本进行训练，只不过输入是一个词向量，不再是2n个词向量。同样看上面的例子：“有力促进了同心县与全国其他地方一道迈向全面小康”，中心词依然取“地方”，n依然取4，则8个训练样本为：

['地方', '同心县'],['地方', '与'],['地方', '全国'],['地方', '其他'],['地方', '一道'],['地方', '迈向'],['地方', '全面'],['地方', '小康']

整个计算过程和图4差别不大，因为输入是一个词向量，所以第一步的平均处理就不再需要了。这里我们可以发现，在训练过程中2n个样本都是一样的，并不会因为谁距离中心词更近或者更远而有不同。虽然Skip-Gram是使用一个词判断前后2n个词，但是根据反向传播和梯度下降机制，在Skip-Gram中是使用前后2n个词来调节一个中心词。所以一般在数据量允许的情况下，使用Skip-Gram会更好。

这里再另外提两点，不知道大家有没有疑问。第一，因为我们拿的是前后2n个词去无序训练，那么在实际预测中，怎么判断每个词的顺序呢？其实，这个问题已经在前面回答过，在模型训练结束以后，我们需要的其实并不是模型本身，而是模型的副产品——词向量，然后拿词向量去做更多的事情（翻译、情感分类、评论分类、智慧客服等），所以一般我们不会使用这个模型去直接处理问题。第二，在Skip-Gram中我们可以发现，一个样本对应了多个label（前后的2n个词），会不会导致无法收敛呢？其实，模型在训练过程中是一个综合调节的过程，模型的目的是为了得到词的特征表达，并不是模型本身，词向量的结果也和你的训练样本有关，通常来说，对于一些专业领域，往往会进行定制化的词向量训练。至于为什么这样处理得到的结果就可以表示每个词，甚至词之间的语义区别，和神经网络一样，目前也是不可解释的。

3.2 Hierarchical Softmax和负采样

前面我们已经介绍了CBOW和Skip-Gram，但是我们可以发现一个问题，就是因为通常情况下词库是非常庞大的（例如汉语有上百万的词），所以导致最后在进行softmax计算的时候，会耗费大量的计算资源，那么有没有可以减少运算成本的处理方法呢？在真实样本中，有些词往往出现的频率更高，有些词出现的频率就会低一些，那么在计算过程中我们是不是可以先判断输出词是不是高频词的概率，如果是，计算结束，如果不是，再判断是不是次高频的词，逐渐依次进行。

3.2.1 哈夫曼树

哈夫曼树和接下来要介绍的东西并没有直接联系，之所以介绍它，是为了能够更好地理解下面的内容，做一个铺垫。哈夫曼树（有些文章中也翻译为霍夫曼树）是一种带权路径长度最短的二叉树，也称为最优二叉树（即所有叶子节点的带权路径和最小）。例如现有一列节点权重数据 [2,5,7,13]，分别构建如图5的二叉树，它们的带权路径长度分别为：

图5a：W = 5*2 + 7*2 + 2*2 + 13*2 = 54

图5b：W = 5*3 + 2*3 +7*2 + 13*1 = 48

可见，图5b的带权路径长度更小，也可以证明图5b就是哈夫曼树（最优二叉树）。

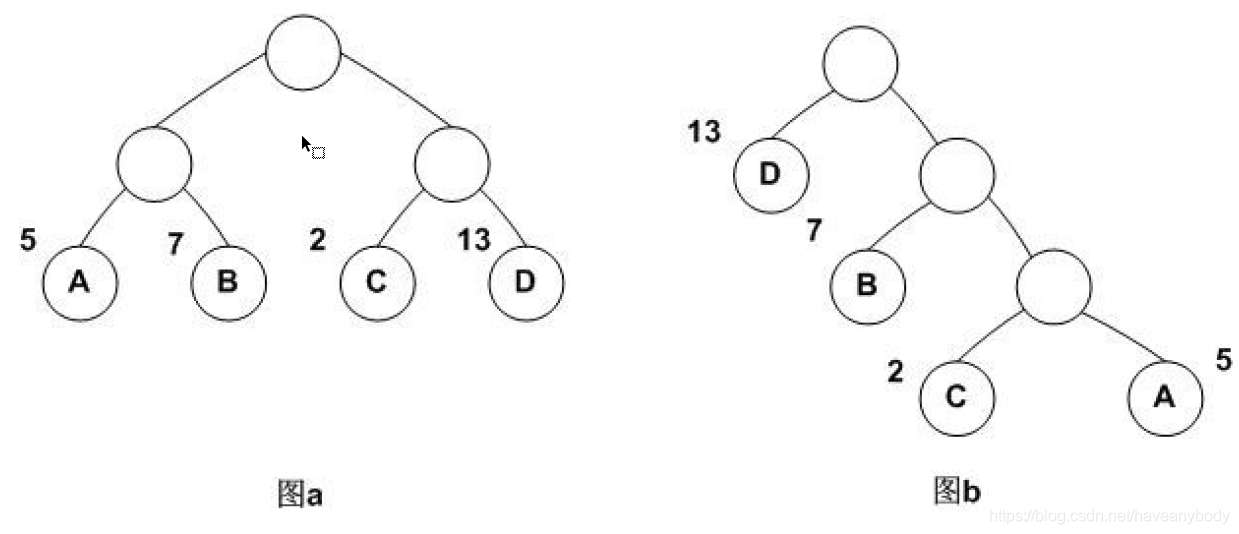
哈夫曼树的建立过程如下：

权值为(w1,w2,...wn)的n个节点，选择权值最小的两个节点进行合并，得到一个新的树，这两个节点分别作为新树的左右子树。新树的根节点权重为左右子树的根节点权重之和。
将之前选择的权值最小的两个节点从森林删除，并把1中生成的新树加入森林。
重复1和2，知道只有一棵树为止。

图5的哈夫曼树构建过程：

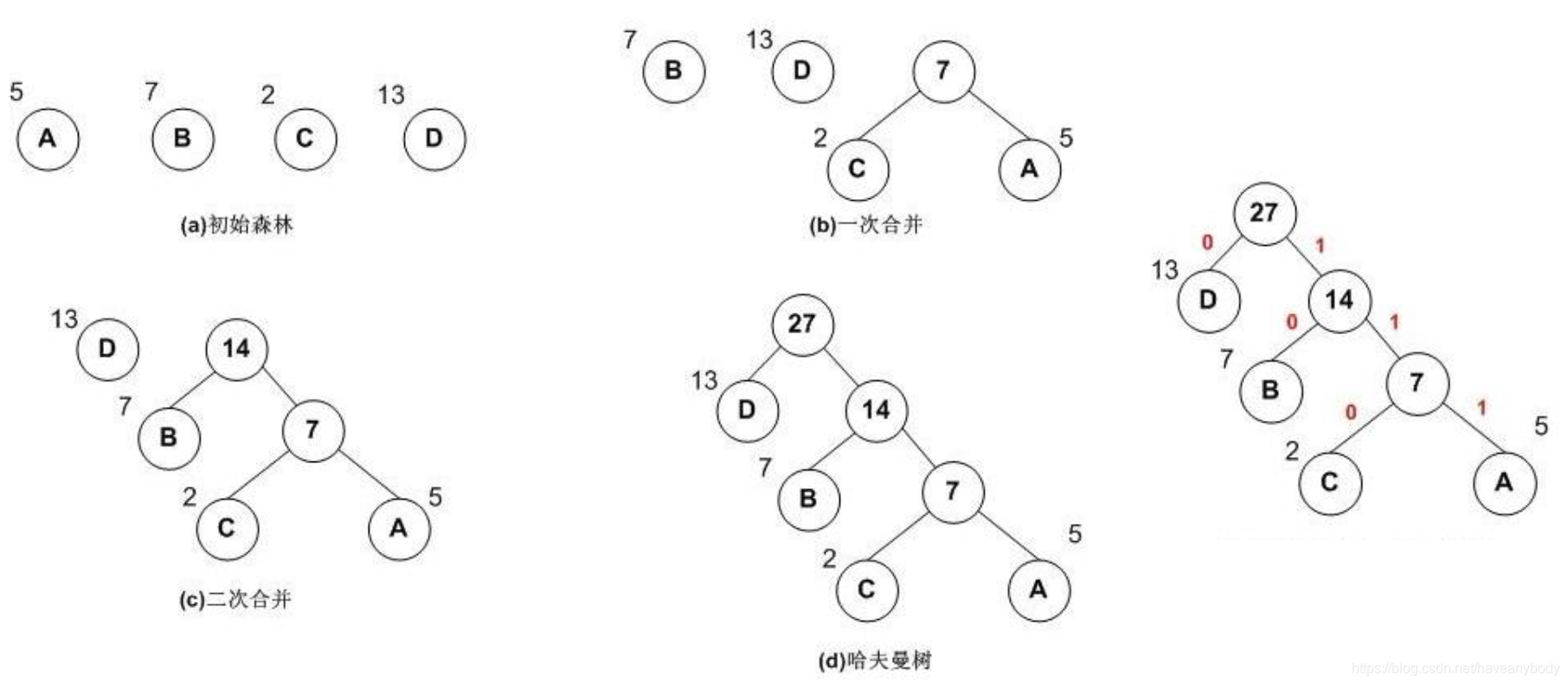
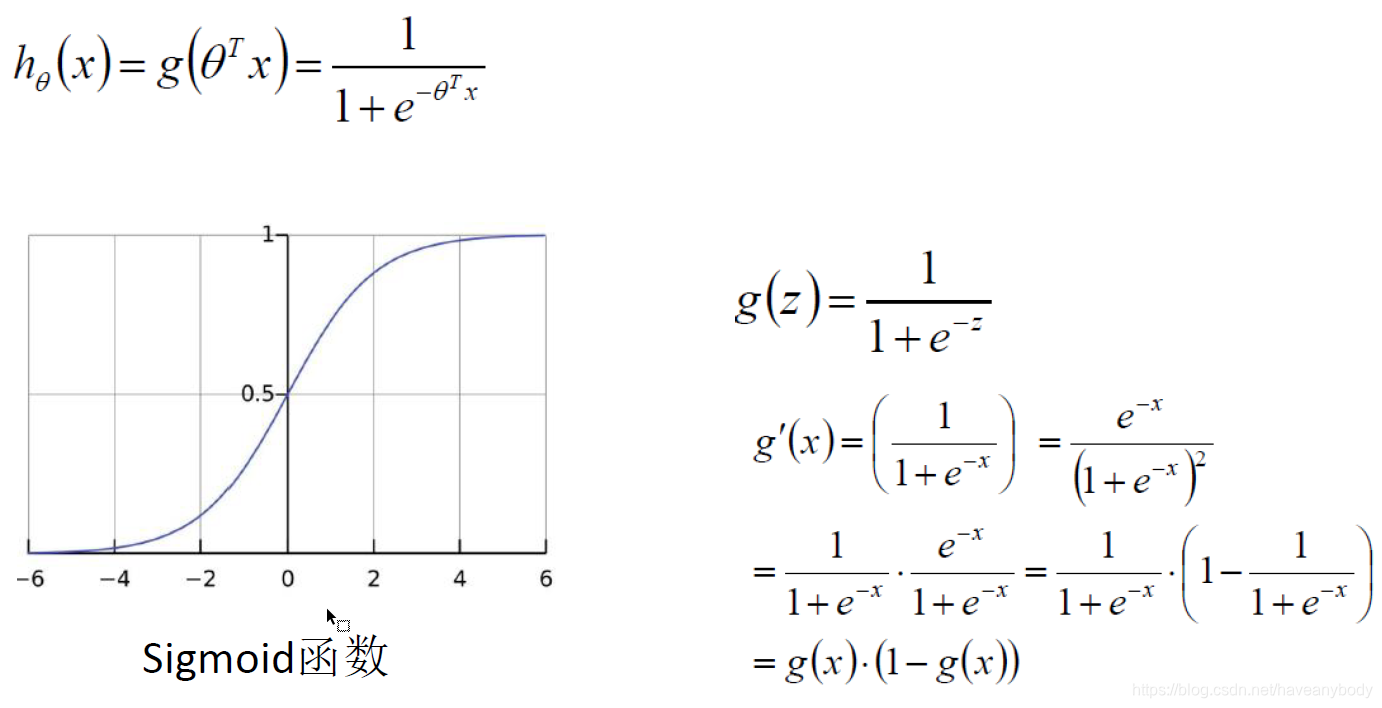
通过构建哈夫曼树，可以对叶子节点进行哈夫曼编码，由于权重高的叶子节点越靠近根节点，而权重低的叶子节点会远离根节点，这样我们的高权重节点编码值较短（路径短），而低权重值编码值较长（路径长）。这保证树的带权路径最短，也符合我们的信息论，即我们希望越常用的词拥有更短的编码。如何编码呢？一般对于一个哈夫曼树的节点（根节点除外），可以约定左子树编码为0，右子树编码为1，如上图。但是在word2vec中，约定编码方式和上面的例子相反，即约定左子树编码为1（负例），右子树编码为0（正例），同时约定左子树的权重不小于右子树的权重。至于为什么这么规定，并没有什么特别的好处，可能只是当年某位大神的习惯操作吧！(｡･ω･｡)

3.2.2 Hierarchical Softmax

在3.2节开始我们已经提到，原始的softmax计算就是一个庞大的多分类问题，计算量大。实际中，有些词出现的频率高，如果计算过程中我们可以优先判断这些词，就能够有效的降低计算量，其实这个逐渐判断的过程就是多次二分类的问题。再看3.2.1介绍的哈夫曼树，是不是也很像一个有多个二分类的分类模型。为了避免要计算所有词的softmax概率，word2vector采用哈夫曼树来代替从隐藏层到输出softmax层的映射（即根据统计词频，构建词库哈夫曼树，叶子节点数量就是词库大小）。我们把所有都要计算的从输出softmax层的概率计算变成了一颗二叉哈夫曼树（频率高的词路径更短），那么我们的softmax概率计算只需要沿着树形结构进行就可以了。如下图所示，我们可以沿着霍夫曼树从根节点一直走到我们的叶子节点（先不要关注图右边的计算过程）。例如“足球”，沿着根节点走 $\theta _{1}$ 、 $\theta _{2}$ 、 $\theta _{3}$ 、 $\theta _{4}$ （路径为1001）即可到达，换句话说，通过四个二分类模型即可得到输出“足球”。可以发现，在哈夫曼树中，隐藏层到输出层的softmax映射不是一下子完成的，而是沿着哈夫曼树结构一步步完成的，因此这种softmax取名为"Hierarchical Softmax"，也叫层级softmax。

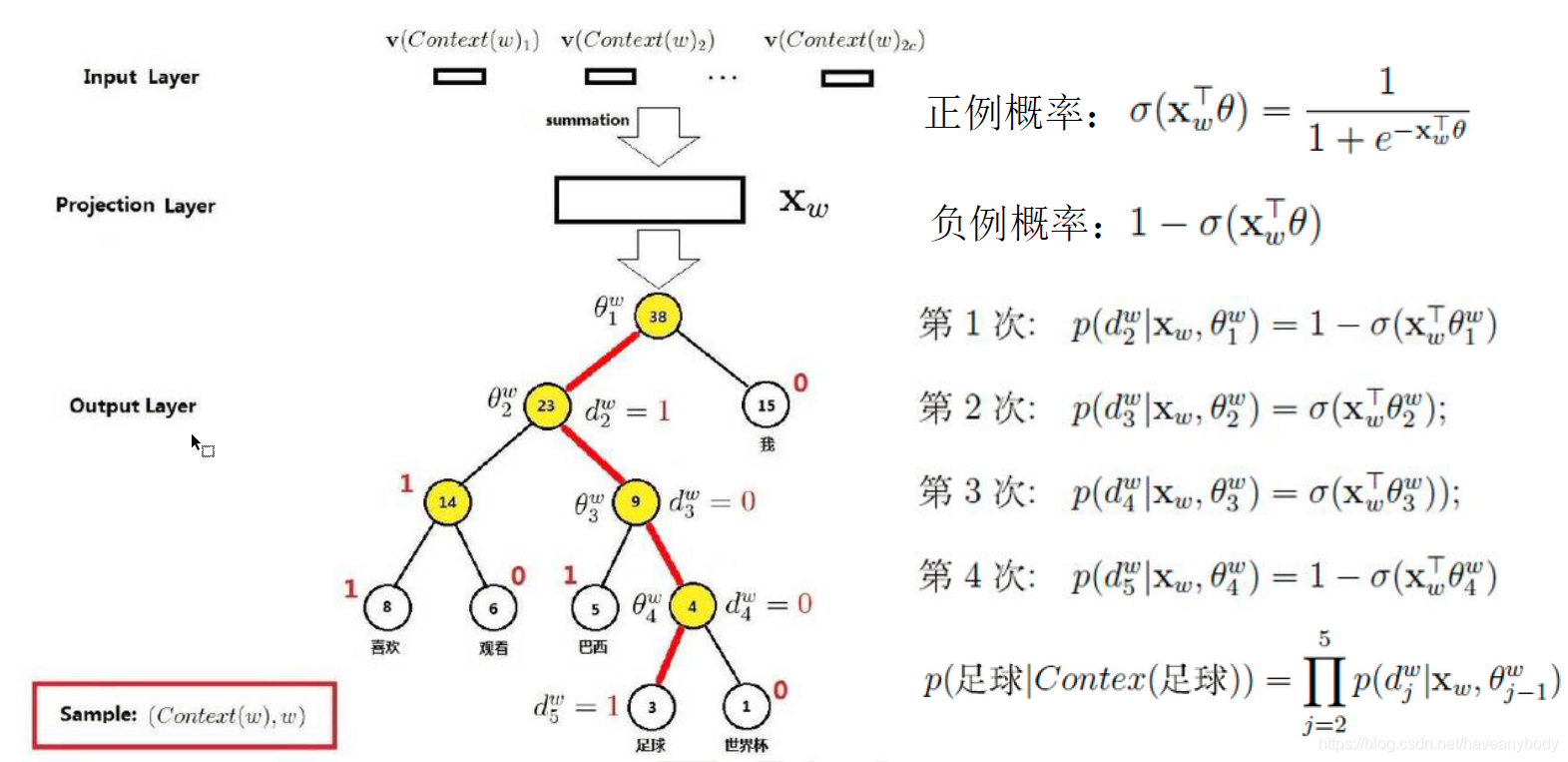
怎么构建这个含有多个二分类模型的哈夫曼树模型呢？这个时候，你是不是想到了某个经典的二分类模型呢？没错，就是逻辑回归，逻辑回归的好处就是模型简单，并且求导方便。到这里，你应该已经明白了Hierarchical Softmax实际上就是训练多个逻辑回归二分类模型的过程。

我们前面已经规定了，左子树为负例，右子树为正例，因此正负例概率分别为：

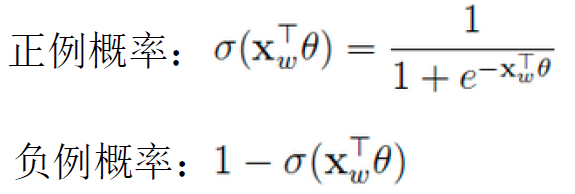
在某一个内部节点，要判断是沿左子树还是右子树走的标准就是看正例和负例谁的概率值大。而控制P概率值大的因素一个是当前节点的词向量X，另一个是当前节点的模型参数θ。现在，我们回去看图7右边的概率计算过程，就一目了然了。对于Hierarchical Softmax本身，目标就是找到合适的所有节点的词向量和所有内部节点θ, 使所有训练样本达到最大似然。

为了方便计算目标求解，我们做下面假设（下面的内容是一些理论补充，对公式没兴趣的同学建议直接跳过）：

则哈夫曼树某一内部节点的逻辑回归概率为（话说CSDN的公式编辑器真难用）：

$p(d_{j}^{w}|X_{w},\theta _{j-1}^{w}) = \left\{\begin{matrix}\sigma (X_{w}^{T}\theta _{j-1}^{w}) \ \ \ d_{j}^{w}=0 \\ 1-\sigma (X_{w}^{T}\theta _{j-1}^{w}) \ \ \ d_{j}^{w}=1 \end{matrix}\right.$

等价于：

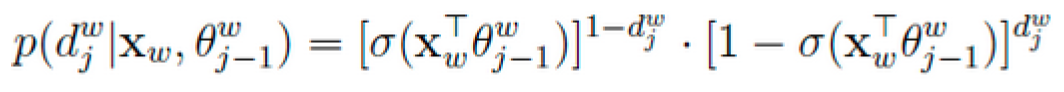
对于某一个叶子节点的最大似然为：

$\prod_{j=2}^{l_w}P(d_j^w|x_w, \theta_{j-1}^w) = \prod_{j=2}^{l_w} [\sigma(x_w^T\theta_{j-1}^w)] ^{1-d_j^w}[1-\sigma(x_w^T\theta_{j-1}^w)]^{d_j^w}$

对数处理：

$L= log \prod_{j=2}^{l_w}P(d_j^w|x_w, \theta_{j-1}^w) = \sum\limits_{j=2}^{l_w} ((1-d_j^w) log [\sigma(x_w^T\theta_{j-1}^w)] + d_j^w log[1-\sigma(x_w^T\theta_{j-1}^w)])$

最大似然估计，采用梯度上升法求解，求偏导如下（ $\eta$ 就是我们常见的学习率）：

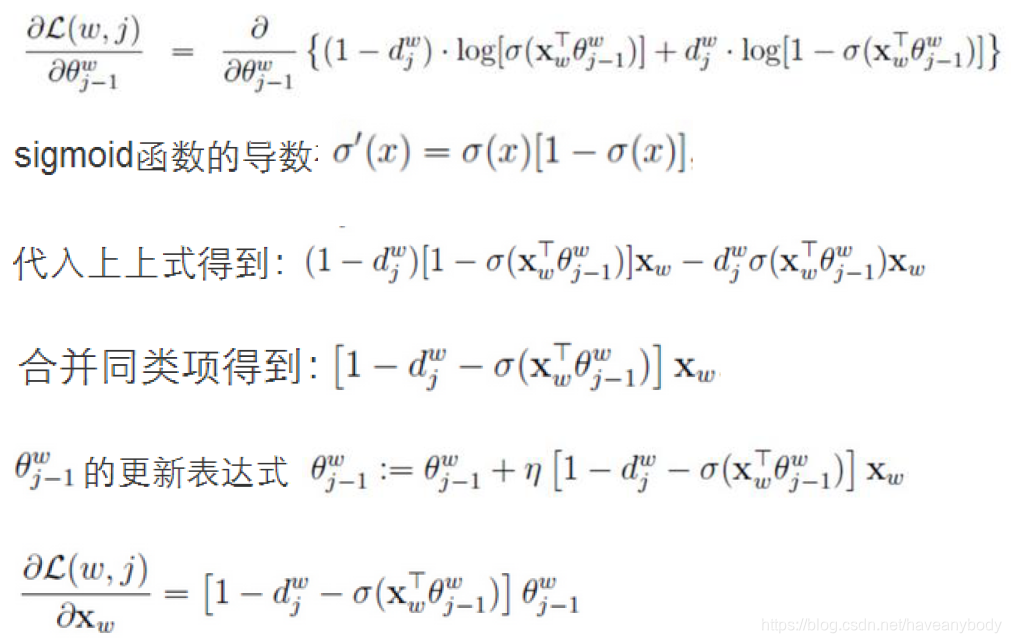
前面在介绍CBOW的时候，第一步计算的时候会首先对2n个输入向量做求和平均处理，word2vector在更新词向量时，会把上面求得的X偏导值更新到每个词向量中。

3.2.3 负采样

前文已经介绍了Hierarchical Softmax针对原始神经网络计算成本高的问题解决方法，但是我们可以发现，针对低频词（靠近根节点的词）计算少了，对于低频词（距离根节点较远的词）依然需要多次计算才行，尤其是当我们的语料库非常大的时候。前面我们说过，因为词库的数量一般都非常大，导致最后的多分类任务计算复杂，主要原因是因为我们一次计算的负例太多（除了目标词，其他词都是负例），那么在计算的时候我们是不是可以减少负例的数量呢？负采样（Negative Sampling）就是这么一种求解word2vector模型的方法，它摒弃了Hierarchical Softmax中构造层级二分类的做法。

假设我们的词库大小是十万，计算的时候除了一个是正例外，其它99999个都是负例，Negative Sampling的做法是，我不再把这99999个负例都拿来参与计算，因为大多数都和当前词没什么关系，只取其中的neg个负例参与计算，利用这一个正例和neg个负例，我们进行二元逻辑回归，得到负采样对应每个词对应的模型参数θ和每个词的词向量，从而降低计算量（实际上就是训练neg+1个二分类模型）。从上面的描述可以看出，Negative Sampling由于没有采用霍夫曼树，每次只是通过采样neg个不同的中心词做负例，就可以训练模型，因此整个过程要比Hierarchical Softmax简单。

在逻辑回归中：

中心词正例应该满足（y=1，表示label为1，正例）： $P(context(w_0), w_i) = \sigma(x_{w_0}^T\theta^{w_i}) ,y_i=1, i=0$

负采样负例应该满足（y=0，表示label为0，负例）： $P(context(w_0), w_i) =1- \sigma(x_{w_0}^T\theta^{w_i}), y_i = 0, i=1,2,..neg$

对于一个训练样本，neg个负例的最大似然如下，同时我们期望最大化：

$\prod_{i=0}^{neg}P(context(w_0), w_i) = \sigma(x_{w_0}^T\theta^{w_0})\prod_{i=1}^{neg}(1- \sigma(x_{w_0}^T\theta^{w_i})) =\prod_{i=0}^{neg} \sigma(x_{w_0}^T\theta^{w_i})^{y_i}(1- \sigma(x_{w_0}^T\theta^{w_i}))^{1-y_i}$

对数处理结果为：

$L = \sum\limits_{i=0}^{neg}y_i log(\sigma(x_{w_0}^T\theta^{w_i})) + (1-y_i) log(1- \sigma(x_{w_0}^T\theta^{w_i}))$

分别求偏导如下（求导过程利用sigmod求导公式）：

$\frac{{\partial L}}{\partial \theta^{w_i}} = y_i(1- \sigma(x_{w_0}^T\theta^{w_i}))x_{w_0}-(1-y_i)\sigma(x_{w_0}^T\theta^{w_i})x_{w_0} = (y_i -\sigma(x_{w_0}^T\theta^{w_i})) x_{w_0}$

$\frac{\partial L}{\partial x^{w_0} } = \sum\limits_{i=0}^{neg}(y_i -\sigma(x_{w_0}^T\theta^{w_i}))\theta^{w_i}$

根据上面偏导结合学习率，利用梯度上升法进行迭代就可以求解我们需要的词向量X和参数 $\theta$ 。

最后，我们还有一个遗留问题没有解决，就是怎么进行采样？如何从所有负例中选择出neg个负例？word2vec采样的方法并不复杂，如果词汇表的大小为V,那么我们就将一段长度为1的线段分成V份，每份对应词汇表中的一个词。当然每个词对应的线段长度是不一样的，高频词对应的线段长，低频词对应的线段短。每个词w的线段长度由其词频决定：

$len(w) = \frac{count(w)}{\sum\limits_{u \in vocab} count(u)}$

分子是该词在训练集中出现的次数，分母是训练集中所有词出现的次数和。在word2vec中，分子和分母都取了3/4次幂如下：

$len(w) = \frac{count(w)^{3/4}}{\sum\limits_{u \in vocab} count(u)^{3/4}}$

在采样前，我们将这段长度为1的线段划分成M等份，这里M>>V，这样可以保证每个词对应的线段都会划分成对应的小块。而M份中的每一份都会落在某一个词对应的线段上。在采样的时候，我们只需要从M个位置中采样出neg个位置就行，此时采样到的每一个位置对应到的线段所属的词就是我们的负例词。可以发现，和Hierarchical Softmax一样，Negative Sampling也认为高频词被采样到的概率更大。当然，在采样过程中会避免出现重复采样的情况，或者可以认为是词库级别的不放回采样。

四、gensim实践

gensim是一款开源的第三方Python工具包，用于从原始的非结构化的文本中，无监督地学习到文本隐层的主题向量表达，主要用于主题建模和文档相似性处理，它支持包括TF-IDF，LSA，LDA，和word2vec在内的多种主题模型算法，在诸如获取单词的词向量等任务中非常有用。gensim的安装也很简单，直接执行 pip install gensim 即可，本节我们使用gensim库和搜狗新闻数据集来训练一个词向量结果，如果需要更大的数据集，可以基于中文维基百科训练。这里之所以使用搜狗新闻数据集，还有一个原因是因为后续还可以使用该数据集做文本分类模型。