AI算法-矩阵分解

1.矩阵分解是什么

矩阵分解，直观上来说就是把原来的大矩阵，近似分解成两个小矩阵的乘积，在实际推荐计算时不再使用大矩阵，而是使用分解得到的两个小矩阵。
如下图：

我们再从机器学习的角度来了解矩阵分解，我们已经知道电影评分预测实际上是一个矩阵补全的过程，在矩阵分解的时候原来的大矩阵必然是稀疏的，即有一部分有评分，有一部分是没有评过分的，不然也就没必要预测和推荐了，所以整个预测模型的最终目的是得到两个小矩阵，通过这两个小矩阵的乘积来补全大矩阵中没有评分的位置。所以对于机器学习模型来说，问题转化成了如何获得两个最优的小矩阵。因为大矩阵有一部分是有评分的，那么只要保证大矩阵有评分的位置（实际值）与两个小矩阵相乘得到的相应位置的评分（预测值）之间的误差最小即可。

2.矩阵分解的原理

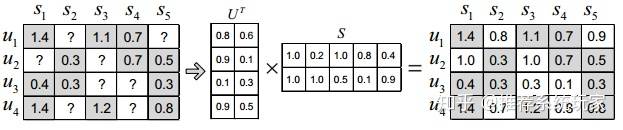
首先来概括的说下矩阵分解的原理。 上图中每一行$u$代表每个用户，每一列$s$代表每个物品，矩阵中的数字代表着用户对物品的打分。？代表着用户没有给这个物品打过分。在实际数据中，我们通过数据构建的矩阵如上图一样并不是一个全部有评分的矩阵。在Netflix真实的数据集里，矩阵的稠密度仅有3%左右。那么就意味着，矩阵中有绝大部分的评分是空白的。如何得到这些空白的评分呢？矩阵分解的就是为了解决这个问题。

矩阵分解算法将$m\times n$维的矩阵$R$分解为$m\times k$的用户矩阵$U$和$k\times n$维的物品矩阵$S$相乘的形式。其中，$m$为用户的数量，$n$为物品的数量，$k$为隐向量（Latent Factor）的维度。$k$的大小决定了隐向量表达能力的强弱，实际应用中，其取值要经过多次的实验来确定。在得到了用户矩阵$U$和物品矩阵$I$后，将两个矩阵相乘，就可以得到一个新的矩阵。那么，我们就对未被评价过的物品，有了一个预测评分。接下来，可以将评分进行排序，推荐给用户。这就是矩阵分解对于推荐系统最基本的用途。

用大白话总结一下，矩阵分解的目的就是通过分解之后的两矩阵内积，来填补缺失的数据，用来做预测评分。矩阵分解的核心是将矩阵分解为两个低维的矩阵的乘积，分别以$k$维的隐因子向量表示，用户向量和物品向量的内积则是用户对物品的偏好度，即预测评分。值得注意的是$k$的选取是通过实验和经验而来的，因此矩阵分解的可解释性不强。

3.矩阵分解的方法

矩阵分解的方法有很多在，这里只介绍我认为最好理解的Funk-SVD。
Funk-SVD的核心思想认为用户的兴趣只受少数几个因素的影响，因此将稀疏且高维的User-Item评分矩阵分解为两个低维矩阵，即通过User、Item评分信息来学习到的用户特征矩阵P和物品特征矩阵Q，通过重构的低维矩阵预测用户对产品的评分。由于用户和物品的特征向量维度比较低，因而可以通过梯度下降(Gradient Descend)的方法高效地求解。
但是Funk-SVD如何将矩阵M分解成为P和Q呢？这里采用了线性回归的思想。我们的目标是让用户的评分和用矩阵乘积得到的评分残差尽可能的小，也就是说，可以用均方差作为损失函数，来寻找最终的P和Q。即通过 User-Item 评分信息来学习到的用户特征矩阵 P 和物品特征矩阵 Q，通过重构的低维矩阵预测用户对物品的评分。

以上述矩阵为例，对于每个用户$u$和物品$i$我们都有一个评分$r_{i,j}$，也就是原始矩阵中有评分的位置，当我们进行分解后，对于每个评分$r$我们都可以用分解后的向量$\hat{r}=q_j^T{p}_i$来近似。我们的目标就是让$\hat{r}\to r$，也就是让$r-\hat{r}=(r_{i,j}-q_j^T{p}_i)$尽可能的小。在这里我们采用均方差作为损失函数：
$Loss=argmin\sum _{i,j}(r_{i,j}-q_j^T{p}_i{)}^2$
为了防止过拟合，我们加入正则化项：
$Loss=argmin\sum _{i,j}(r_{i,j}-q_j^T{p}_i{)}^2+(||p_i||+||q_j||{)}^2$

4.具体步骤

1.首先我们要定义一个类似于上图的评分矩阵，用$R$表示，其维度为$N\times M$，也就是$R$为$N$行$M$列矩阵。
然后我们将其分解$P$矩阵与$Q$矩阵，其中$P$矩阵维度为$N\times K$，$Q$矩阵维度为$K\times M$
于是我们可以得到
$R\approx$ $\hat{R}=P\times Q$
对于$P$，$Q$ 矩阵的解释，直观上，$P$ 矩阵是$N$ 个用户对$K$ 个主题的关系，$Q$ 矩阵是$K$ 个主题跟$M$ 个物品的关系，至于$K$ 个主题具体是什么，在算法里面$K$ 是一个参数，需要调节的，通常$10\sim 100$ 之间。

2.对于$\hat{R}$矩阵：
${\hat{r}}_{ij}=p_i^T{q}_j=\sum _{k=1}^K{p}_{ik}{q}_{kj}$
$\hat{R}$与$R$的维度相同，其中${\hat{r}}_{ij}$是$\hat{R}$第$i$行第$j$列的元素值。

3.求损失函数并更新变量：
使用原始的评分矩阵$R$ 与重新构建的评分矩阵$\hat{R}$ 之间的误差的平方作为损失函数，即：
$e_{ij}^2=(r_{ij}-{\hat{r}}_{ij}{)}^2=(r_{ij}-\sum _{k=1}^K{p}_{ik}{q}_{kj}{)}^2$
通过梯度下降法，更新变量：
求导：$$\frac{\partial }{{\partial }_{pik}}{e}_{ij}^2=-2(r_{ij}-\sum _{k=1}^K{p}_{ik}{q}_{kj})q_{kj}=-2e_{ij}{q}_{kj}$$$$\frac{\partial }{{\partial }_{qkj}}{e}_{ij}^2=-2(r_{ij}-\sum _{k=1}^K{p}_{ik}{q}_{kj})p_{ik}=-2e_{ij}{p}_{ik}$$
根据负梯度的方向更新变量：$$p_{ik}^{\prime }=p_{ik}-\alpha \frac{\partial }{\partial p_{ik}}{e}_{ij}^2=p_{ik}+2\alpha e_{ij}{q}_{kj}$$$$q_{kj}^{\prime }=q_{kj}-\alpha \frac{\partial }{\partial q_{kj}}{e}_{ij}^2=q_{kj}+2\alpha e_{ij}{p}_{ik}$$

4.在损失函数中加入正则化惩罚项：通常在求解的过程中，为了能够有较好的泛化能力，会在损失函数中加入正则项，以对参数进行约束。加入正则项后的计算过程如下：$$E_{ij}^2=(r_{ij}-\sum _{k=1}^K{p}_{ik}{q}_{kj}{)}^2+\frac{\beta }{2}\sum _{k=1}^K(p_{ik}^2+q_{kj}^2)$$通过梯度下降法，更新变量：求导：$$\frac{\partial }{\partial p_{ik}}{E}_{ij}^2=-2(r_{ij}-\sum _{k=1}^K{p}_{ik}{q}_{kj})q_{kj}+\beta p_{ik}=-2e_{ij}{q}_{kj}+\beta p_{ik}$$$$\frac{\partial }{\partial q_{kj}}{E}_{ij}^2=-2(r_{ij}-\sum _{k=1}^K{p}_{ik}{q}_{kj})p_{ik}+\beta q_{kj}=-2e_{ij}{p}_{ik}+\beta q_{kj}$$根据负梯度的方向更新变量：$$p_{ik}^{\prime }=p_{ik}-\alpha (\frac{\partial }{\partial p_{ik}}{e}_{ij}^2+\beta p_{ik})=p_{ik}+\alpha (2e_{ij}{q}_{kj}-\beta p_{ik})$$$$q_{kj}^{\prime }=q_{kj}-\alpha (\frac{\partial }{\partial q_{kj}}{e}_{ij}^2+\beta q_{kj})=q_{kj}+\alpha (2e_{ij}{p}_{ik}-\beta q_{kj})$$
5.算法终止：每次更新完 $\hat{R}$ 后，计算一次$loss$ 值，若$loss$ 值非常小或者到达最大迭代次数，结束算法。于是就得到了我们最终的预测矩阵 $\hat{R}$。

5.代码实现

import numpy as np
import math
import matplotlib.pyplot as plt

#定义矩阵分解函数
def Matrix_decomposition(R,P,Q,N,M,K,alpha=0.0002,beta=0.02):
    Q = Q.T #Q 矩阵转置
    loss_list = [] #存储每次迭代计算的 loss 值
    for step in range(5000):
        #更新 R^
        for i in range(N):
            for j in range(M):
                if R[i][j] != 0:
                    #计算损失函数
                    error = R[i][j]
                    for k in range(K):
                        error -= P[i][k]*Q[k][j]
                    #优化 P,Q 矩阵的元素
                    for k in range(K):
                        P[i][k] = P[i][k] + alpha*(2*error*Q[k][j]-beta*P[i][k])
                        Q[k][j] = Q[k][j] + alpha*(2*error*P[i][k]-beta*Q[k][j])
                    
        loss = 0.0
        #计算每一次迭代后的 loss 大小，就是原来 R 矩阵里面每个非缺失值跟预测值的平方损失
        for i in range(N):
            for j in range(M):
                if R[i][j] != 0:
                    #计算 loss 公式加号的左边
                    data = 0
                    for k in range(K):
                        data = data + P[i][k]*Q[k][j]
                    loss = loss + math.pow(R[i][j]-data,2)
                    #得到完整 loss 值
                    for k in range(K):
                        loss = loss + beta/2*(P[i][k]*P[i][k]+Q[k][j]*Q[k][j])
                    loss_list.append(loss)
        plt.scatter(step,loss)
        #输出 loss 值
        if (step+1) % 1000 == 0:
            print("loss={:}".format(loss))
        #判断
        if loss < 0.001:
            print(loss)
            break
    plt.show()    
    return P,Q
        
if __name__ == "__main__":
    N = 5
    M = 4
    K = 5
    R = np.array([[5,3,0,1],
                [4,0,0,1],
                [1,1,0,5],
                [1,0,0,4],
                [0,1,5,4]]) #N=5,M=4
    print("初始评分矩阵：")
    print(R)
    #定义 P 和 Q 矩阵
    P = np.random.rand(N,K) #N=5,K=2
    Q = np.random.rand(M,K) #M=4,K=2
    
    print("开始矩阵分解：")
    P,Q = Matrix_decomposition(R,P,Q,N,M,K)
    print("矩阵分解结束。")
    print("得到的预测矩阵：")
    print(np.dot(P,Q))

6.矩阵分解的优缺点

1.优点

1.比较容易编程实现，随机梯度下降方法依次迭代即可训练出模型。比较低的时间和空间复杂度，高维矩阵映射为两个低维矩阵节省了存储空间，训练过程比较费时，但是可以离线完成；评分预测一般在线计算，直接使用离线训练得到的参数，可以实时推荐。
2.预测的精度比较高，预测准确率要高于基于领域的协同过滤以及内容过滤等方法。
3.非常好的扩展性，很方便在用户特征向量和物品特征向量中添加其它因素，例如添加隐性反馈因素的SVD++，；添加时间动态Time SVD++，此方法将偏置部分和用户兴趣都表示成一个关于时间的函数，可以很好的捕捉到用户的兴趣漂移。

2.缺点

1.模型训练比较费时。
2.推荐结果不具有很好的可解释性，分解出来的用户和物品矩阵的每个维度无法和现实生活中的概念来解释，无法用现实概念给每个维度命名，只能理解为潜在语义空间。
参考文献1
参考文献2
参考文献3