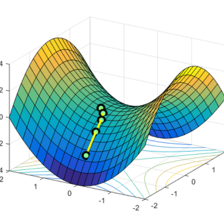
机器学习中的优化方法
机器学习,尤其现在比较热的深度学习,针对某个学习任务得到损失函数,需要优化网络的参数,以减小损失函数,所使用的技术手段是梯度下降等最优化的方法。因此,学习最优化的方法,了解其本质,对损失函数设计和调参,具有重要的指导意义!
何雷
小码农,辛勤耕耘每一寸土地
展开
-
浅析深度学习中优化方法
目前而言,深度学习是机器学习的发展前沿,一般针对大数据量的学习目标。其优化方法来源于基本的机器学习的优化方法,但也有所不同。下面,小结一下,其基础是随机梯度下降的方法,但是为了学习的自适应性,做了如下改进:1. 因为每次训练的数据不一样,可能导致目标函数的梯度变化剧烈,为了解决这个问题,联合上次迭代的梯度和当前梯度,使梯度变化变缓(指数衰减);2. 在学习过程中,当迭代结果接近最优值时,我们需要学原创 2017-01-12 17:02:01 · 3422 阅读 · 0 评论 -
浅析深度学习mini_batch的BP反传算法
在深度学习中,如果我们已经定义了网络,输入,以及输出,那么接下来就是损失函数,优化策略,以及一般由框架完成的BP反传。这篇博文我们主要探讨一下深度的BP反传算法(以梯度下降为例),尤其是mini_batch的BP反传,目标是如何更新网络的参数:权重和偏置。 首先,我们来看网络中基本参数的一些定义。 使用梯度下降法,一般计算所有样本的损失函数的原创 2016-11-25 09:19:03 · 6524 阅读 · 1 评论 -
浅析无约束优化的方法
在讨论函数的极值问题时,我们一般使用二次正定函数来推导。为什么只是二次呢?这里引用吴福朝老师的话说:“光滑函数或二阶可微函数,在极值点的局部范围内,在相差高阶无穷小的情况下,都可以表示为二次函数,极值是局部性质,这就理所当然地,用局部二次taylor展开来讨论函数的极值了。”说得很精妙!吴老师是我们实验室神级别的人物,但是很低调!http://vision.ia.ac.cn/Faculty/ind原创 2016-12-07 17:05:57 · 1778 阅读 · 1 评论 -
浅析机器学习中的一维直线搜索
针对一个机器学习的优化问题,假设我们使用梯度下降的方法求解最优点。一般地,在初始点和可行下降方向确定后,我们要沿着可行下降方向确定步长(或学习率),这个时候,就要使用到一维搜索的方法。一维搜索的方法分为精确搜索的方法和非精确的搜索方法。非精确的搜索方法即确定一个沿可行下降方向上的步长,使目标函数下降即可;而精确的搜索方法求解出最优的步长,通过公式推导,由最优步长得到的新点的梯度与搜索方向正交,如下原创 2016-12-02 10:37:35 · 3403 阅读 · 0 评论
 分享
分享