简说期望类问题的解法

近年的acm竞赛中，数学期望问题常有涉及，在以前也常让本人感到很头疼，近来突然开窍，掌握了基本的分析方法，希望对大家有帮助。写得浅薄，可能数学上不够严谨，只供理解。

首先，来看下期望有啥基本的公式。

对离散型随机变量x，其概率为p，有

$$E(x)=\sum _{ i }^{ }{ { p }_{ i }{ x }_{ i } }$$

对随机变量A、B有

$$E(\alpha A\pm \beta B)=\alpha E(A)\pm \beta E(B)$$

第二条式子是今天的主角，他表明了期望有线性的性质，简单理解就是期望之间可根据关系，简单运算（不严谨的理解）。这就为我们解决一个期望问题，不断转化为解决另外的期望问题，最终转化到一个已知的期望上。

例1

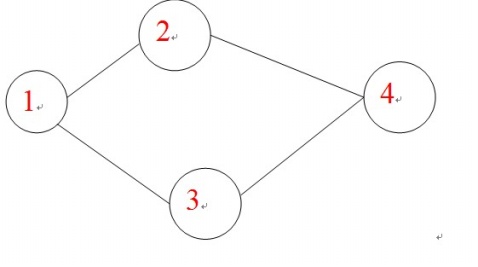
举一个求期望最简单的例子，见下图。

假设有个人在 1号节点处，每一分钟他会缘着边随机走到一个节点或者在原地停留，问他走到4号节点需要平均几分钟？

这是个简单的期望问题，我们用 $E_{i}\quad (i=1,2,3,4)$ 表示从i号节点走到4号节点的数学期望值。根据题意对1号节点有
$E_1=(1/3)*E_1+(1/3)*E_2+(1/3)*E_3+1$ ①

表示他下一分钟可以走到2或者3或在原地1，每个可能概率是1/3 ,注意是下一分钟，故要加上1.

同理我们对节点2，3同样可以列出

$E_2=(1/3)*E_1+(1/3)*E_2+(1/3)*E_4+1$ ②
$E_3=(1/3)*E_1+(1/3)*E_3+(1/3)*E_4+1$ ③

那$E_4$等于多少呢？ 很明显$E_4=0$ ④，因为他就是要到点4

这样上面1234式其实就是组成了一组方程组，解方程组就可得出$E_1$，用高斯消元，复杂度是$O(n^3)$

从上述例子，我们可总结出如何解决期望类问题，根据题意，表示出各个状态的期望（上例的$E_{i}\quad (i=1,2,3,4)$），根据概率公式，列出期望之间的方程，解方程即可。

例2

下面看用上述思路如何解决一道题（poj2096）

题意：

一个人受雇于某公司要找出某个软件的bug和子组件，这个软件一共有$n$个bug和$s$个子组件，每次他都能同时随机发现$1$个bug和$1$个子组件，问他找到所有的bug和子组件的期望次数。

我们用$E(i,j)$表示他找到了$i$个bug和$j$个子组件，离找到$n$个bug和$s$个子组件还需要的期望次数，这样要求的就是$E(0,0)$，而$E(n,s)=0$，对任意的$E(i,j)$。
1次查找4种情况：
1. 没发现任何新的bug和子组件
2. 发现一个新的bug
3. 发现一个新的子组件
4. 同时发现一个新的bug和子组件
用概率公式可得：

$E(i,j)=1+(i*j/n/s)*E(i,j)+(i*(s-j)/n/s)E(i,j+1)+((n-i)*j/n/s)*E(i+1,j)+(n-i)*(s-j)/n/s*E(i+1,j+1)$

移项可得：

$(1-(i*j)/(n*s))E(i,j)=1+(i*(s-j)/n/s)E(i,j+1)+((n-i)*j/n/s)*E(i+1,j)+(n-i)*(s-j)/n/s*E(i+1,j+1)$

这样根据边界就可解出所有的$E(i,j)$，注意因为当我们找到n个bug和s个子组件就结束，对$i>n 或 j>s$均无解的情况，并非期望是0 (数学上常见问题，0和不存在的区别)

那这题是否也是要用高斯消元呢？ 用高斯消元得话复杂度是$O(n^3)$，达到$10^{18}$ 根本是不可解的！

但其实，注意观察方程，当我们要解$E(i,j)$的话就需要$E(i+1,j),E(I,j+1),E(i+1,j+1)$，一开始已知$E(n,s)$，那其实只要我们从高往低一个个解出$i,j$就可以了！ 即可根据递推式解出所有的$E(i,j)$ 复杂度是$O(n^2)$ ，完美解决。

$my$ $code$

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 2005;
double dp[N][N];

int main() {
    int n, s;
    while(~scanf("%d%d", &n, &s)) {
        memset(dp, 0, sizeof(dp));
        for(int i = n; i >= 0; i--) {
            for(int j = s; j >= 0; j--) {
                if(i == n && j == s) continue;
                double p = 1.0 - (double)(i * j) / (n * s);
                dp[i][j] += (double) (n - i) * (s - j) / (n * s) * dp[i+1][j+1];
                dp[i][j] += (double) i * (s-j) / (n * s) * dp[i][j+1];
                dp[i][j] += (double) (n - i) * j / (n * s) * dp[i+1][j];
                dp[i][j] = (dp[i][j] + 1.0) / p;
            }
        }
        printf("%.4f\n", dp[0][0]);
    }
    return 0;
}

从上面这道题，我们再次看到了解决期望问题的思路，而且是用到了递推解决问题，其实可递推的原因，当我们把各个状态当成是一个个节点时，概率关系为有向边，我们可看到，可递推的问题其实就是这个关系图是无环的！那必须要用方程组解决的问题其实就是存在环！ 而且我还要指出的是用高斯消元的时候，要注意误差的问题，最好把式子适当的增大，避免解小数，否则误差太大，估计也会卡题。