第四章 不定积分-my write

目录

1. 原函数和不定积分

1.1 存在原理

1.2 但不连续也可能存在原函数

1.3  不定积分的性质

1.4 不定积分基本公式 （背

2. 第一换元积分法 凑微分 

3. 第二换元积分法 换元法 

​4. 分部积分法

4.1 比较适用于两类不同函数相乘

4.2 多项式 与 eax/ sin ax/ cosax，将e和三角函数部分放进dx

4.3 多项式和lnx / arctanx / arcsinx，把多项式放进dx

4.4 e 与 sinx / cosx

5. 三类常见可积函数积分

5.1 有理函数积分

5.2 三角有理式积分

---

1. 原函数和不定积分

原函数 Fx+C
不定积分 ∫fxdx=Fx+C

1.1 存在原理

1.2 但不连续也可能存在原函数

1.3  不定积分的性质

d∫与∫d： ∫ 1 dg(x) = g(x) + C， d∫g(x) = g(x)
∫ (fx±gx) dx可拆成两部分
∫ k·fx dx常数可先提

1.4 不定积分基本公式 （背

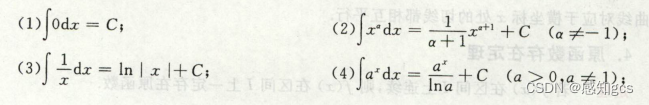
2. 第一换元积分法 凑微分 

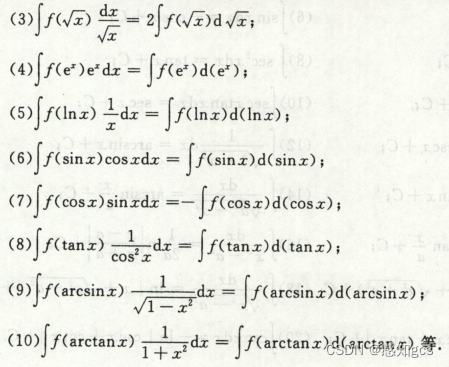
3. 第二换元积分法 换元法 

还有直接令的形式，t = 根号下1+e2

4. 分部积分法

4.1 比较适用于两类不同函数相乘

4.2 多项式 与 eax/ sin ax/ cosax，将e和三角函数部分放进dx

4.3 多项式和lnx / arctanx / arcsinx，把多项式放进dx

4.4 e 与 sinx / cosx

把e放进dx，但是不能一步做出来

5. 三类常见可积函数积分

5.1 有理函数积分

分母分解因式，分子分母同乘凑微分

5.2 三角有理式积分