集总电路的基本定律——基尔霍夫定律

目录

1.支路、结点、回路的概念

2.基尔霍夫定电流定律（KCL）

★广义KCL

3.基尔霍夫电压定律（KVL）

4.基尔霍夫定律的基础性和适用性

挑战★★★★★

---

出生于柯尼斯堡（今俄罗斯加里宁格勒）的德国物理学家古斯塔夫·罗伯特·基尔霍夫（Gustav Robert Kirchhoff，1824.03～1887.10）于21岁时（1845年）发表了自己的第一篇论文，提出了求解复杂电路（网络）的两个定律，即基尔霍夫电流定律（KCL）和基尔霍夫电压定律（KVL），解决了阻碍当时电气技术发展的复杂电路分析难题。有的资料中以基尔霍夫第一定律和基尔霍夫第二定律进行表述，分别指的是KCL和KVL。

基尔霍夫（G. R. Kirchhoff）

1.支路、结点、回路的概念

⑴支路：电路中每个二端元件称为一条支路，串联的元件可视为一条支路。

⑵结点：亦称节点，是指支路与支路的连接点。

⑶回路：由支路构成的闭合路径称为回路。

2.基尔霍夫定电流定律（KCL）

定义：在集总电路中，任何时刻，对任一结点，流出该结点的所有支路电流的代数和为零。

KCL是电荷守恒法则运用于集总电路的结果。

将上述定义中的“流出”换成“流入”，KCL的含义不变。

列KCL代数方程时，可规定“流出”或“流入”为正方向，以确定代数式中各项前的正负号，例如第k条支路电流的参考方向与规定的正方向一致，则式中取，否则取。

KCL也可以理解为：在一个结点处，进入该结点的电流之和等于离开该结点的电流之和。所以实际使用时，可根据各支路电流的参考方向，以流出等于流入的等式形式列写方程。

★广义KCL

KCL不仅适用于电路中的结点，对电路中包含几个结点的闭合面（广义节点）也同样适用。

题1图1所示电路中，，计算和。

图1

解析：对封闭面S（图2）列KCL方程，有

，得。

图2

对标示结点列KCL，得

题2电路如图3所示，试求电流I。

图3

解析：标注原电路如图4所示，对结点①列KCL方程，得

图4

对虚线所示闭合面列KCL方程，有

所以。

3.基尔霍夫电压定律（KVL）

定义：在集总电路中，任何时刻，沿任一回路的所有支路（或元件）电压（降）的代数和为零。

KVL是能量守恒法则和电荷守恒法则共同运用于集总电路的结果。

列KVL代数方程时，可指定回路的绕行方向，以确定代数式中各项前的正负号，各元件电压的参考方向与绕行方向一致，则前面取“+”，否则取“-”。

4.基尔霍夫定律的基础性和适用性

集总电路的电压、电流变量受到两类约束。一类是元件特性造成的自身约束，体现为VCR；另一类是由电路连接（元件的相互连接）所引起的支路电流之间或支路电压之间的约束关系，即拓扑约束（也称几何约束），这正是KCL和KVL所体现的，它们对元件没有要求，只要是集总电路总是成立的。

因此，基尔霍夫定律是集总参数电路的基本定律，KCL和KVL只跟电路的连接方式有关，而与元件的性质无关，无论是线性的还是非线性的，时变的还是非时变的，它们都成立。

题3电路如图5所示，已知一端口网络、，其中发出功率为1W，吸收功率为2W，，，求的值。

图5

解析：标注电路如图6所示。

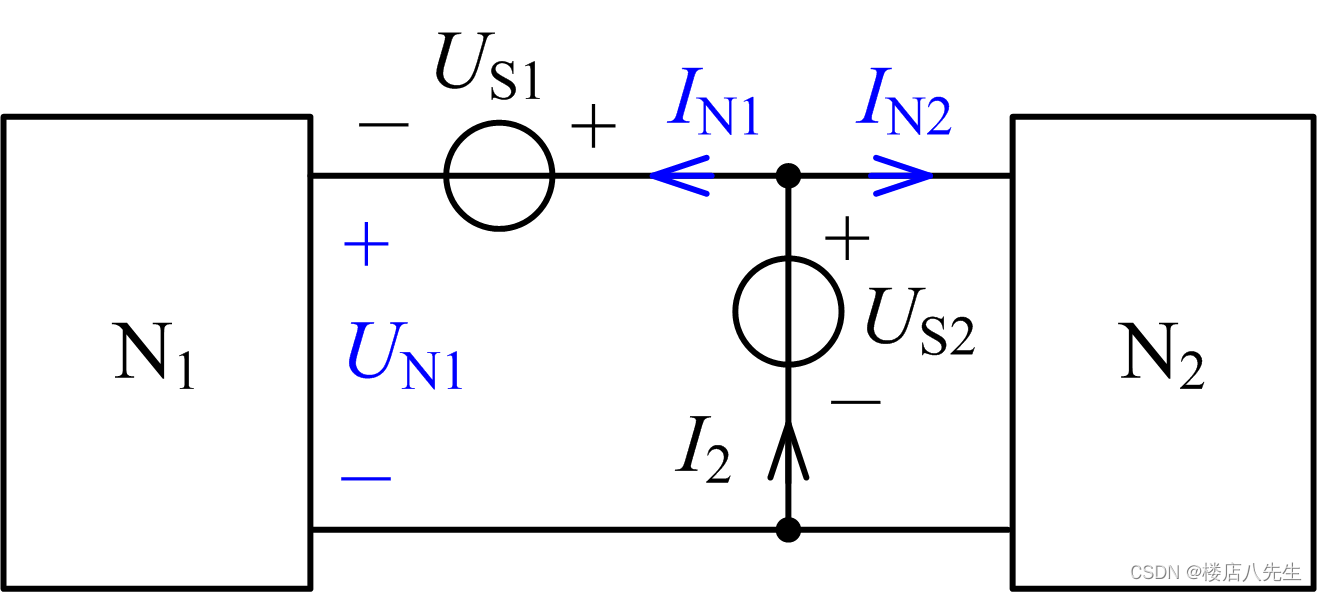
图6

吸收功率为2W，则

，求得

（KCL）

又，得

根据KVL，。

题4求图7所示电路中独立电压源和独立电流源的功率，并分别说明它们是实际发出功率还是实际吸收功率。

图7

解析：根据KCL，标注原电路如图8所示。由KVL，列方程

图8

解得

故2A电流源发出功率为

；

10V电压源发出功率为

。

题5如图9所示电路中，已知U=2V，求I和R的值。

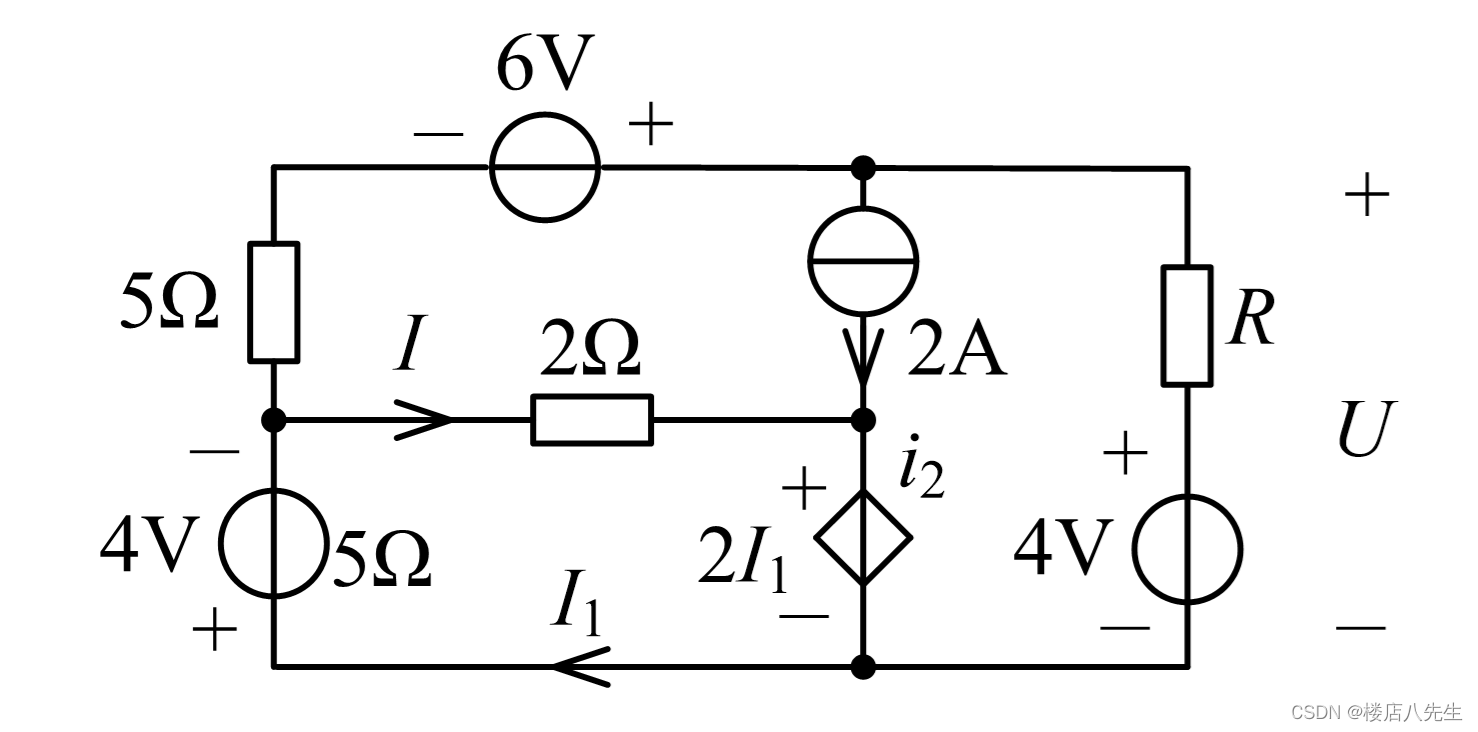
图9

解析：设流过R的电流为，标注电路如图10所示。

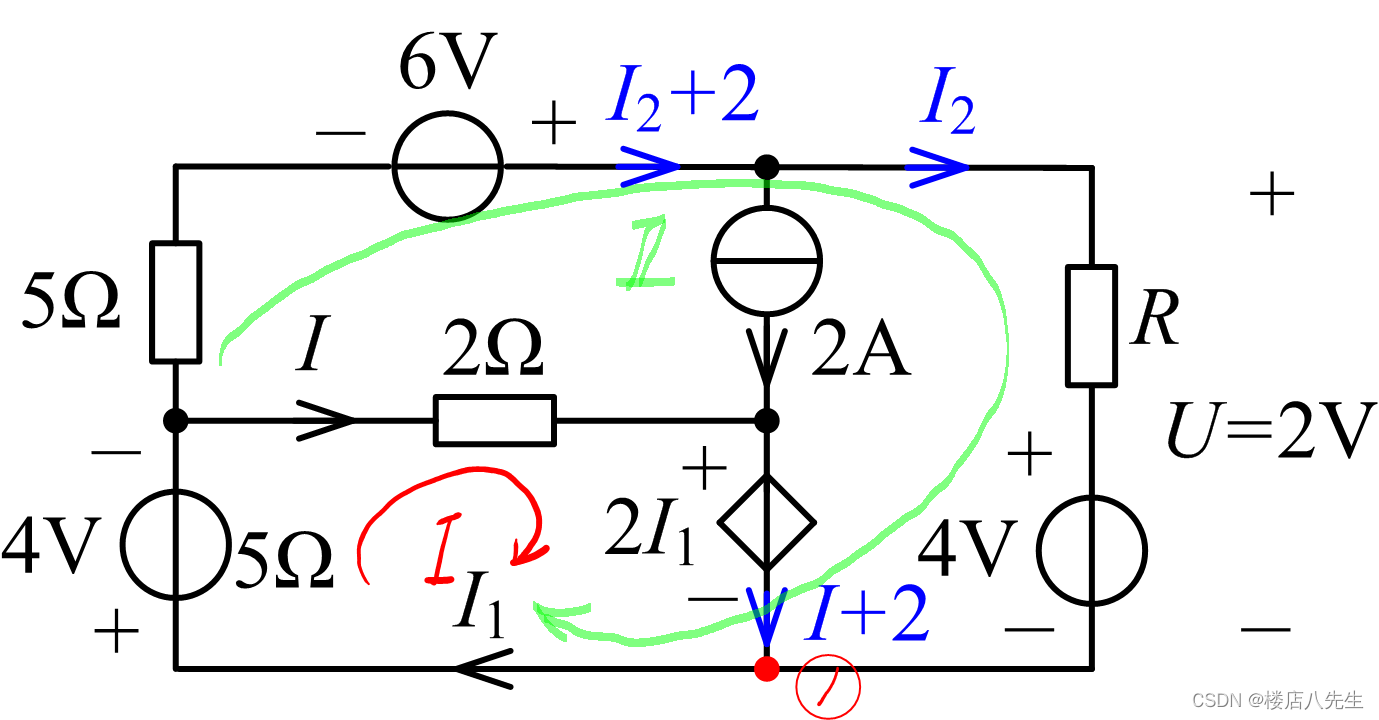
图10

对回路Ⅰ和回路Ⅱ列KVL方程，对结点①列KCL方程

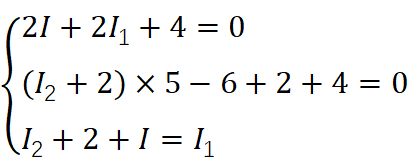
解得

挑战★★★★★

题6计算图11所示电路中各独立电源提供的功率。

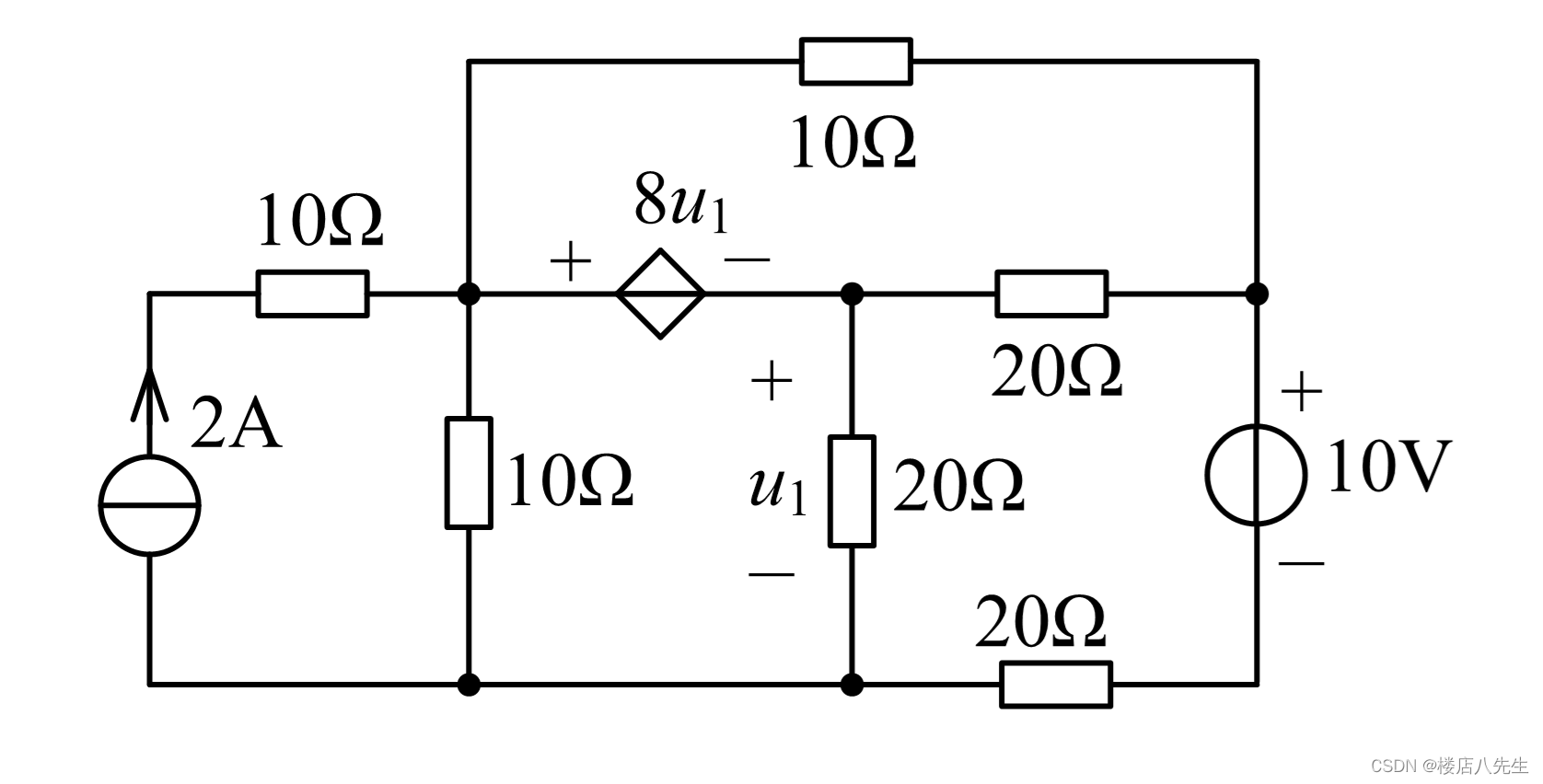
图11

解析：标注各支路电流，如图12所示。

图12

由电阻VCR，易得；

列结点0和结点①的KCL方程，有

列回路Ⅰ、回路Ⅱ、回路Ⅲ的KVL方程，有

联解以上6个方程，得

，

2A电流源提供的功率为

；

10V电压源提供的功率为

（实际吸收功率）。