递推之平面分割问题【图文超详细】

学生说应该改成【图文超不详细】，不愧是我的好学生呐！

什么是递推？

递推法是一种重要的数学方法，在数学的各个领域中都有广泛的运用，也是计算机用于数值计算的一个重要算法。这种算法特点是：一个问题的求解需一系列的计算，在已知条件和所求问题之间总存在着某种相互联系的关系，在计算时，如果可以找到前后过程之间的数量关系(即递推式)，那么，从问题出发逐步推到已知条件，此种方法叫逆推。无论顺推还是逆推，其关键是要找到递推式。这种处理问题的方法能使复杂运算化为若干步重复的简单运算，充分发挥出计算机擅长于重复处理的特点。

递推算法的首要问题是得到相邻的数据项间的关系(即递推关系)。递推算法避开了求通项公式的麻烦，把一个复杂的问题的求解，分解成了连续的若干步简单运算。一般说来，可以将递推算法看成是一种特殊的迭代算法。

可用递推算法求解的题目一般有以下两个特点：
1、问题可以划分成多个状态；
2、除初始状态外，其它各个状态都可以用固定的递推关系式来表示。
在我们实际解题中，题目不会直接给出递推关系式，而是需要通过分析各种状态，找出递推关系式。

一、直线分割平面问题(切蛋糕)

题意：n条直线，最多可以把平面分为多少个区域。

思路：f[n]表示n条直线最多可以划分出f[n]个区域，那么f[n]如何而来？

先退一步f[n-1]表示n-1条直线最多可以划分出f[n-1]个区域，那么f[n]=f[n-1]+第n条直线最多可以划分的区域。问题就转移到第n条直线的加入最多可以划分的区域，要适当第n条直线尽可能的和前面已经有的n-1条直线都有交点，第n条直线上就会出现n-1个交点，这些交点将第n条直线划分成n-2个线段和两端的两条射线，而每条线段和射线都可以将原来的区域进一步一分为二，新出现了(n-2)+2个区域，即n个区域。

我们可以用同样的方法进行减而治之，将问题规模不同的缩小至f[1]:

f[n]=f[n-1]+n=f[n-2]+(n-1)+n=……=f[1]+2+……+(n-2)+(n-1)+n，f[1]可以作为边界条件停止，f[1]显然为2；故f[n]=1+（1+2+……+n）=1+n(n+1)/2;

如果用递推公式一步步迭代计算答案的话，用即可，不需要再费心力算出最终的数学公式。当然，从之前学习的复杂度分析来看，递推公式的复杂度为，而最终的公式只需要。

总结：

1、初始条件f[1]=2;

2、每个状态直接都可以用固定的递推式来表示。

二、折线分割平面

题意：n条折线，最多可以把平面分为多少个区域。

思路：f[n]表示n条折线最多可以划分出f[n]个区域，那么f[n]如何而来？和前面推导一样，这里简写了。

f[n]=f[n-1]+第n条折线最多可以划分的区域，观察图片，第n条折线的每条射线都可以最多和之前已经存在的n-1条折线（也就是2*（n-1）射线）产生2*（n-1）个交点，进而被划分成n-1条线段和1条射线，所以一条折线可以带来两倍的交点、线段、射线，分别是4*（n-1）个交点、4*（n-1）条线段、2条射线。

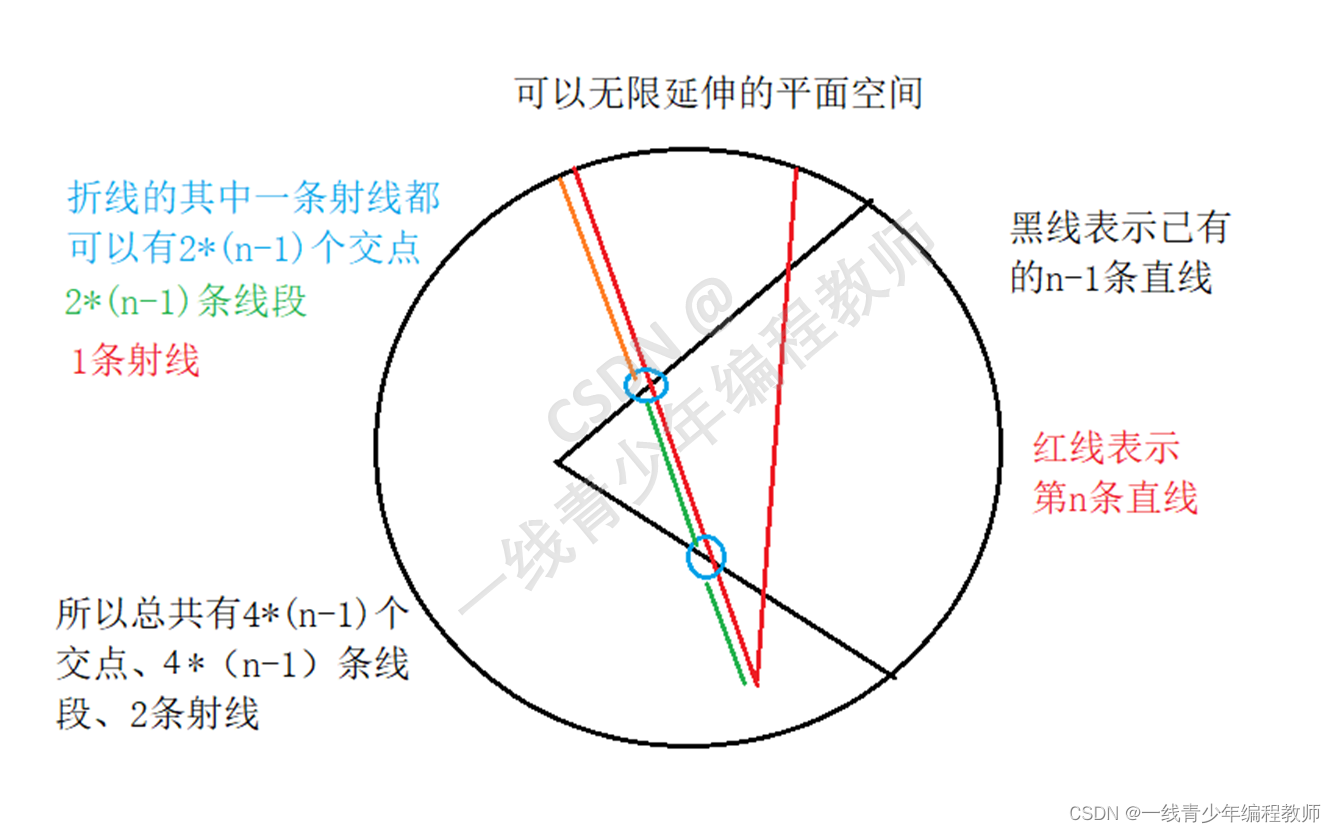
我们知道每条线段和射线都可以将原有的区域一分为二，那么就可以增加4*（n-1）+2个区域，但是需要注意的是，折线的转折点相邻的两条线段仅能新划分出一个区域，故最总增加了4*（n-1）+1个区域。由此，f[n]=f[n-1]+4n-3。

继续用同样的方法进行减而治之，将问题规模不同的缩小至f[1]:

f[n]=f[n-1]+4n-3=f[n-2]+4(n-1)-3+4n-3=……=f[1]+4*2-3+4*3-3+4*4-3+……4n-3=

总结：

1、初始条件f[1]=2;

2、每个状态直接都可以用固定的递推式来表示。

三、封闭曲线切割平面

题意：有n条封闭曲线画在平面上，而任何两条封闭曲线恰好相交于两点，问这些封闭曲线最多把平面分割成的区域个数。

思路：f[n]表示n条封闭曲线可以最多可以划分f[n]个区域。

f[n]同样可以看出由两部分组成，前n-1条封闭曲线分割的区域（即f[n-1]）和第n条封闭曲线新增的区域。写成f[n]=f[n-1]+第n条封闭曲线新增的区域。

那么第n条曲线最多可以新增多少区域呢？看图，第n条曲线可以和前n-1条曲线产生2*（n-1）个交点，将第n条曲线分割成2*（n-1）条线段，而每条线段都可以将原先的区域一分为二，共新增2*（n-1）个区域。所以有递推式：f[n]=f[n-1]+2(n-1)。和上述递推式一样，可以化简成数学公式：。

总结：

1、初始条件f[1]=2;

2、每个状态直接都可以用固定的递推式来表示。

四、三角形分割平面

题意：有n个三角形画在平面上，最多把平面分割成的区域个数。

思路：f[n]表示n个三角形最多可以划分f[n]个区域。

f[n]=f[n-1]+第n个三角形新增的区域，第n个三角最多可以新增多少个区域呢？看图，第n个三角形的每条边都可以和之前的n-1个三角形产生2（n-1）个交点，这些交点将这条边分割成2（n-1）+1条线段，那么第n个三角形最多被分割成6（n-1）+3条线段，除了三角形的三个角两边的线段仅能构成一个新区域之外，其余的每条线段都将原来的区域一分为二，故总共新增了6（n-1）+3-3个区域，递推式为：f[n]=f[n-1]+6(n-1)。化简成最终公式为：

总结：

1、初始条件f[1]=2;

2、每个状态直接都可以用固定的递推式来表示。

五、平面分割空间（二维-->三维）

题意：有n个平面，最多可以将三维空间划分多个三维区域

思路：f[n]表示n个平面最多可以将三维空间划分成f[n]个区域。

f[n]=f[n-1]+第n个平面新划分的区域个数，那么第n个平面新划分的区域个数怎么求呢？

由二维的分割问题可知，平面分割与线之间的交点有关，即交点决定射线和线段的条数，从而决定新增的区域数。 试想在三维中则是否与平面的交线有关呢？要有最多的空间数，则第n个平面需与前n-1个平面相交，且不能有共同的交线（即最多有n-1 条交线）。而n-1条直线最多把一个平面（第n个平面）分割成多少个区域呢？答案就在我们在第一个问题中，最多1+n(n-1)/2个区域。

所以，递推式为f[n]=f[n+1]+1+n(n-1)/2，可以化简成f[n]=(n^3+5n)/6+1

总结：

1、初始条件f[1]=2;

2、每个状态直接都可以用固定的递推式来表示。